А = 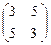 . Найдем собственные значения матрицы А:
. Найдем собственные значения матрицы А:
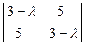 = 0, (3 - l)2 – 25 = 0, l2 - 6 l – 16 = 0,
= 0, (3 - l)2 – 25 = 0, l2 - 6 l – 16 = 0,
l1 = -2, l2 = 8 – cобственные числа. Так как l1 и l2 отличны от нуля и разных знаков, то кривая – гипербола.
Найдем собственные векторы матрицы А.
Пусть l = l1 = -2.
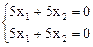 Þ х1 = -х2 Þ
Þ х1 = -х2 Þ 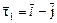 .
.
| 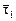 | =
| = 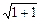 =
= 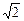 ,
, 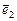 =
= 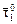 =
= 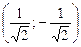 =
= 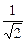 (
(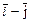 ).
).
Пусть l = l2 = 8.
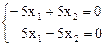 Þ х1 = х2 Þ
Þ х1 = х2 Þ 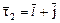 .
.
| 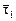 | =
| = 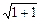 =
= 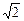 ,
, 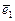 =
= 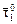 =
= 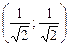 =
= 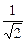 (
(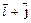 ).
).
Выполняя преобразование
х = 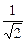 (х¢ - у¢), у =
(х¢ - у¢), у = 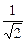 (х¢ + у¢),
(х¢ + у¢),
матрицей которого является матрица
С = 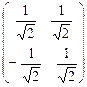 ,
,
получим
8 (х¢)2 – 2 (у¢)2 - 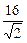 х¢ -
х¢ - 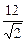 у¢ - 13 = 0.
у¢ - 13 = 0.
Выделим полные квадраты по каждой из новых переменных:
8 (х¢)2 - 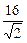 х¢ = 8
х¢ = 8 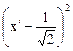 - 4
- 4
– 2 (у¢)2 - 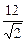 у¢ = -2
у¢ = -2 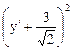 + 9.
+ 9.
Уравнение кривой примет вид:
8 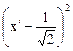 - 2
- 2 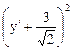 = 8.
= 8.
Сделаем замену переменных, соответствующую сдвигу по каждой из координатных осей:
х² = х¢ - 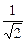 , у² = у¢ +
, у² = у¢ + 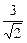 .
.
Получим уравнение кривой:
8 (х²)2 – 2 (у²)2 =8 или 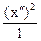 -
- 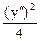 = 1.
= 1.
Это и есть результирующее уравнение гиперболы.
Результирующее преобразование координат имеет вид:
х = 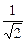 (х¢ - у¢), где х¢ = х² +
(х¢ - у¢), где х¢ = х² + 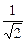 , у¢ = у² -
, у¢ = у² - 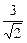 , т.е.
, т.е.
х = 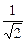
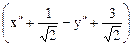 =
= 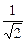 (х² - у²) + 2
(х² - у²) + 2
у = 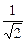 (х¢ + у¢) =
(х¢ + у¢) = 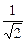
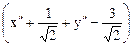 =
= 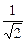 (х² + у²) – 1,
(х² + у²) – 1,
а каноническая система координат:
|
|
|
0¢ (2, -1), 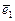 =
= 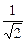
 -
- 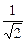
 ,
, 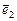 =
= 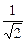
 +
+ 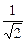
 .
.
 2015-01-07
2015-01-07 309
309








