Два события A и B называются независимыми, если
P (A Ç B) = P (A) P (B). (7)
Для пояснения естественности такого определения вернемся к теореме умножения вероятностей (6) и установим, в каких ситуациях из нее следует (7). Очевидно, что это может быть тогда, когда условная вероятность P (A | B) равна соответствующей безусловной вероятности события А: P (A | B) = P (A), то есть когда вероятность события А не зависит от того, произошло событие В или нет. (Аналогично, P (B | A) = P (B)).
В основе независимости событий лежит их физическая независимость, состоящая в том, что множества факторов, влияющих на исход эксперимента и обусловливающих появление этих событий, не пересекаются или почти не пересекаются.
События A 1, A 2,…, An называются независимыми в совокупности, если вероятность каждого из этих событий не зависит от появления любого числа остальных событий.
Теорема умножения вероятностей для независимых в совокупности событий A 1, A 2,…, An имеет вид
P (A 1 Ç A 2 Ç … Ç An) = P (A 1) P (A 2) … P (An).
Пример 17 В трех урнах находятся шары разного цвета. В первой – два черных, пять белых и три красных, во второй – три черных, три белых и четыре красных, в третьей – один черный, четыре белых и пять красных. Из каждой урны случайным образом вынимают по одному шару. Найти вероятность того, что среди трех вынутых шаров окажутся:
|
|
|
а) только черные шары;
б) все шары одного цвета.
Решение. Обозначим события:
Ai = {выбран черный шар из i -й урны}, i = 1, 2, 3;
Вi = {выбран белый шар из i -й урны}, i = 1, 2, 3;
Сi = {выбран красный шар из i -й урны}, i = 1, 2, 3;
D = {среди трех вынутых шаров окажутся только черные шары};
Е = {среди трех вынутых шаров окажутся шары одного цвета}.
| Количество шаров | Урна | |
| № 1 | № 2 | № 3 |
| 2 черных, 5 белых, 3 красных | 3 черных, 3 белых, 4 красных | 1 черный, 4 белых, 5 красных |
Согласно условию вероятность события A 1 P (A 1) = 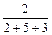 =
= 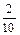 , вероятность события A 2 – P (A 2) =
, вероятность события A 2 – P (A 2) = 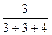 =
= 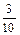 , вероятность события A 3– P (A 3) =
, вероятность события A 3– P (A 3) = 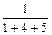 =
= 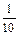 .
.
Так как события Ai (i = 1, 2, 3) – независимы, применим теорему умножения вероятностей независимых событий, получим
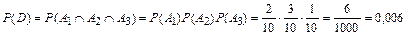 .
.
Событие Е можно представить в виде 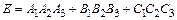 . События
. События 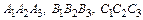 несовместные.
несовместные.
Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
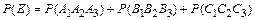 = 0,006 + 0,06 + 0,06 = 0,126, где
= 0,006 + 0,06 + 0,06 = 0,126, где 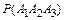 =
= 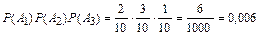 ;
;
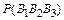 =
= 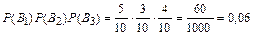 ;
;
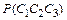 =
= 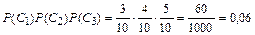 .
.
Пример 18 При изготовлении изделие проходит три основные независимые операции. Вероятность получения стандартного изделия при первой операции равна 0,9, второй – 0,95, третьей – 0,8. Найти вероятность того, что:
а) изделие окажется стандартным;
б) изделие окажется нестандартным.
Решение. Обозначим события:
A i = { i -ю операцию изделие прошло без брака}, i = 1, 2, 3;
|
|
|
B = {изделие окажется стандартным};
C = {изделие окажется нестандартным}.
Согласно условию вероятность события A 1 P (A 1) = 0,9, вероятность события A 2– P (A 2) = 0,95, вероятность события A 3 – P (A 3) = 0,8.
Тогда вероятности противоположных событий: 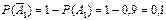 ,
, 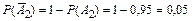 ,
, 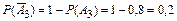 .
.
Определим все элементарные события данного случайного эксперимента и соответствующие вероятности:
| Элементарные события | События | Вероятности |
| 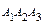
| 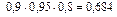
|
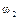
| 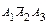
| 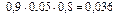
|
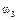
| 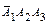
| 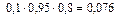
|
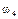
| 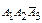
| 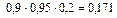
|
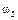
| 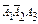
| 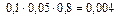
|
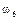
| 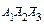
| 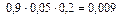
|
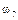
| 
| 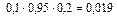
|
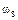
| 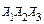
| 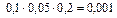
|
| Итого | 
|
а) По теореме умножения вероятностей независимых событий 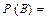
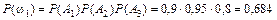 .
.
б) Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
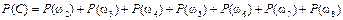 = =
= = 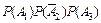
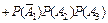
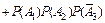 +
+ 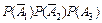 +
+
+ 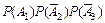
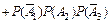 +
+ 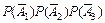 = 0,036 + 0,076 + + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316.
= 0,036 + 0,076 + + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316.
События B = {изделие окажется стандартным} и C = {изделие окажется нестандартным} являются противоположными, то есть 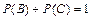 ,
,
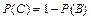 = 1 – 0,684.
= 1 – 0,684.
 2015-01-07
2015-01-07 1171
1171








