Теория гомоморфизма дает возможность строить упрощенные модели
систем. Упрощение должно выполнятся таким образом, чтобы новая система
была либо эквивалентна оригиналу, либо являлась его достаточно хорошей
аппроксимацией.
Две системы эквивалентны при одинаковой совокупности входных воздействий, если они имитируют одинаковые выходные сигналы.
Системы для которых существует преобразование, приводящее к эквивалентной более простой системе, называются упрощаемыми, а свойство - упрощаемостью. При этом параметры более простой системы в функциональной связи с параметрами исходной. Не всякая система может быть упрощена. В этом случае возникает задача аппроксимации исходной системы. При аппроксимации параметры исходной и аппроксимированной систем не связаны функциональными зависимостями. Аппроксимация осуществляется с некоторой точностью, определяемой критерием аппроксимации. Не всегда аппроксимация является упрощением.
Пример: 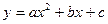 , кусочно-линейная аппроксимация.
, кусочно-линейная аппроксимация.
Вывод: всякую систему нужно попытаться упростить либо путем поиска более простой эквивалентной, либо аппроксимирезющей.
Задание №6. Задача о размещении буйков в акватории береговой линии. (ПЗ-2)
Задано.
1.Карта акватории.
2.Количество буйков (например - 100).
Необходимо.
В условиях полного отсутствия какой-либо информации о гидрологических характеристиках акватории, простейшим образом разместить буйки для проведения начальных исследований акватории.
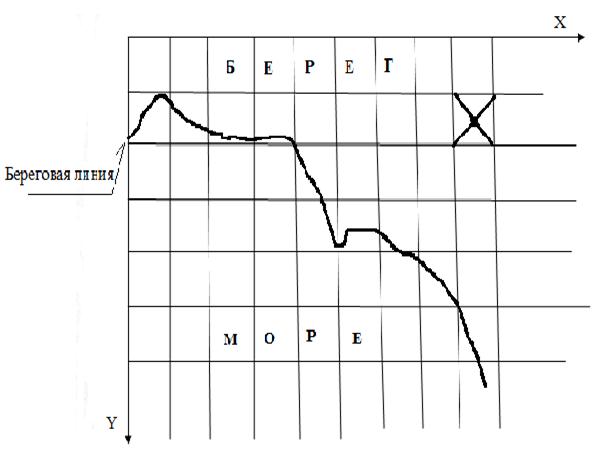
Рис. 8.
Логика системы и упрощение Эшби
Повышение размерности задачи приводит к более богатым свойствам, однако, это повышение значительно усложняет анализ и синтез сложных систем. Одним из направлений в решении этой проблемы является, алгебраический метод, предложенный французской школой Н. Бурбаки и Риге.
Этот метод дает алгебру, которая может быть использована не только как
алгебра, но также за счет формы, в которой она развита, способна показать, что в наших рассуждениях является логичным, операционным либо структурой соотношений. До сих пор эти понятия могли быть выражены только словесно (приблизительно).
В основе алгебры лежит понятие гомоморфизма и суть ее сводится к соотношениям вида:
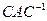 - некоторая алгебраическая форма, которая всегда может рассматриваться как ответ на вопрос:
- некоторая алгебраическая форма, которая всегда может рассматриваться как ответ на вопрос:
на что будет похожа система А после кодирования ее операцией типа С?
Пример:
Последовательность событий.
Рассмотрим основную идею системы, поведение которой определено ее состоянием. Пусть λ - отображение, которое описывает фактическое поведение системы так, что в момент времени t + наблюдаемое состояние λ(t)→η
σ - операция, соответствующая переходу σ→t+Δt или σ(t)→t+1, для дискретных моментов времени.
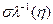 - запаздывающие моменты времени.
- запаздывающие моменты времени.
Тогда происходящее в системе 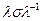 - множество состояний системы, следующих за состоянием η.
- множество состояний системы, следующих за состоянием η.
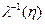 - совокупность всех моментов времени, в которых производятся
- совокупность всех моментов времени, в которых производятся
наблюдения.
В каждый момент времени (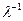 ), отстоящий от предыдущего на интервал времени (σ) производится наблюдение состояний системы
), отстоящий от предыдущего на интервал времени (σ) производится наблюдение состояний системы
λ
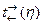
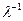
Свойства системы, определяемой состоянием
1. Для каждого из возможных состояний 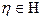 , производится наблюдение этих состояний в моменты времени, отстоящие один от другого на единицу изменения времени:
, производится наблюдение этих состояний в моменты времени, отстоящие один от другого на единицу изменения времени:
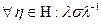
2. Упрощение.
Под упрощением в большинстве случаев понимается применение некоторого отношения эквивалентности, которое собирает состояния в такое подмножество, в котором обмен происходит только между ними.
Известно, что только некоторые состояния эквивалентности дают упрощенную форму, сохраняющую свойства системы.
Предположим, что система μ и отношение R обладают свойством совместимости, т.е. отображение R собирает все состояния системы. Образуя множество Rμ(η).
Условием совместимости является наличие того фактора, что множество μ[R(η)] содержится в предыдущем множестве, т.е.
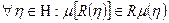
последнее равнозначно
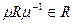 .
.
Предполагается, что: 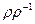 - формула отношения эквивалентности.
- формула отношения эквивалентности.
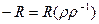 - упрощающее отображение,
- упрощающее отображение,
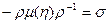 - упрощенное обобщение системы.
- упрощенное обобщение системы.
В последнем случае существует функциональное отношение. Всякое отношение, которое удовлетворяет условию 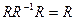 не является отображением, но может быть сделано таковым, если применить к его образу подходящее отношение эквивалентности. Это является непосредственным указанием на возможность упрощения.
не является отображением, но может быть сделано таковым, если применить к его образу подходящее отношение эквивалентности. Это является непосредственным указанием на возможность упрощения.
3. Декомпозиция (выделение части из целого).
Систему μ можно рассматривать как такое множество τ переменных
состояний, в 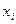 пределах которого связи между переменными многочисленны и
пределах которого связи между переменными многочисленны и
количество связей между этими и другими множествами есть величина меньшего порядка.
Пусть система, выделяемая внутри некоторой большой системы, обладает указанным выше свойством.
При решении задачи декомпозиции необходимо математически выразить связаны или не связаны две части системы:
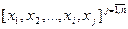 , где
, где 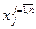 - подсистема и каждая часть
- подсистема и каждая часть 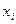 задается множествами элементов
задается множествами элементов 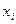 , таким образом, что состояние системы в целом определяется комплексным набором
, таким образом, что состояние системы в целом определяется комплексным набором
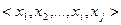
В качестве системы мы определили μ – отображения в себя.
Пусть множество частей будет 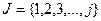 , тогда
, тогда 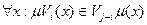 , т.е.
, т.е. 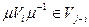
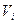 - оператор, переводящий вектор внутрь множества всех возможных состояний, составляющих отображения R (подмножества I) (собирает все состояния системы).
- оператор, переводящий вектор внутрь множества всех возможных состояний, составляющих отображения R (подмножества I) (собирает все состояния системы).
Последняя запись указывает на то, что переменная i не оказывает непосредственного влияния на переменную j.
4.Изолированная система (закрытая).
Если каждая пара (i,j) испытана на связь, то можно использовать множество пар для определения Q функциональных связей.
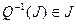
 - закрытая система;
- закрытая система;
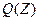 - множество переменных, влияющих на Z частей, где Z=I-J, а
- множество переменных, влияющих на Z частей, где Z=I-J, а 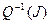 - множество всех переменных, влияющих на J.
- множество всех переменных, влияющих на J.
5. Координация
1. Одноуровневые, одноцелевые системы
2. Одноуровневые, многоцелевые системы
3. Многоуровневые, многоцелевые системы.
В системах (2 и 3) возникает понятие конфликта цели. Во втором случае конфликт цели в общем случае неразрешим, потому что в системах нет приоритета. В системах 3-го типа могут быть модели, которые позволяют устранить конфликт цели с помощью координации, например, путем введения обратных связей (в общем случае - информационных).
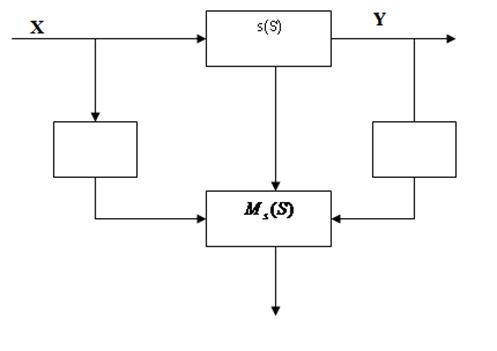
Рис. 9.
Основанием для классификации моделей является цель моделирования. Целевая ориентация моделей позволяет классифицировать их по типам целей, по способам воспроизведения (реализации), по изменению на различных этапах жизненного цикла.
По типам целей различают модели:
- познавательные;
- прагматические.
По способам воспроизведения различают модели:
- идеальные (абстрактные);
- материальные (реальные, физические).
По изменению во времени различают модели:
- статические,
- динамические.
2.3.1 Познавательные и прагматические модели
Различие познавательных и прагматических моделей проявляется в их отношении к оригиналу в процессе деятельности.
Познавательные модели являются формой организации и представления знаний, по средством соединения новых знаний с имеющимися. Если в процессе создания познавательной модели некоторого реального объекта наблюдаются расхождения, то осуществляется коррекция модели с целью приблизить ее к реальности.
Примерами познавательных моделей являются, по существу, все научные теории, которые развиваются и совершенствуются по мере выявления несоответствия старых моделей реалиям мира. Например, познавательные модели в социологии связаны с изучением закономерностей
социального развития, тенденцией изменения различных социальных явлений.
Прагматические модели являются средством управления практическими действиями, способом представления требуемых действий или их результата, т. е. являются рабочим представлением цели. Поэтому в случае обнаружения расхождения между прагматической моделью и реальным объектом основные усилия должны быть направлены на коррекцию (изменение) реальности.
Прагматические модели носят нормативный характер, выполняют роль стандарта, образца, под который подгоняются реальные объекты
Примером таких моделей служат программы, уставы, кодексы законов, чертежи, шаблоны и т. п. Например, некоторые прагматические модели в социологии предназначены для разработки практических рекомендаций и предложений по повышению эффективности управления различными социальными процессами
Классификация описанных кратко моделей представлена на рис.10.
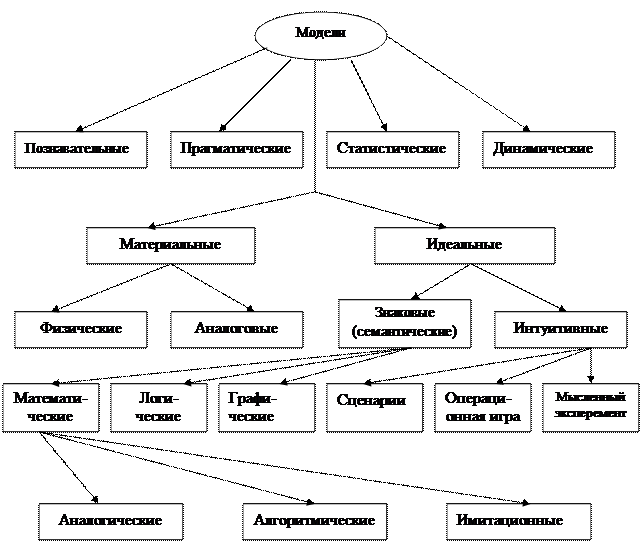
Рис. 10. Классификация моделей
Семантика – (франц. – semantique, от греч. semanticos – обозначающий,
sёma - знак).
 2014-09-02
2014-09-02 874
874







