Квадратурные формулы Ньютона-Котеса

Если для функции 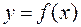требуется вычислить интеграл 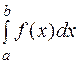, то разобьем отрезок 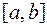на 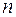равных частей с шагом 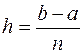, где 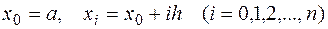. Значения заданной функции в точках равны: 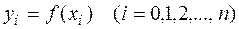. По заданным значениями 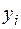построим полином Лагранжа 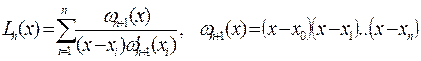, где .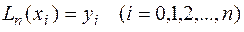

Заменяя интегрируемую функцию полиномом Лагранжа, получим равенство 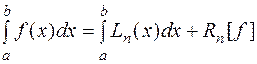, где 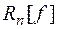- ошибка квадратурной формулы (остаточный член). Подставив выражение для полинома Лагранжа, получим приближенную квадратурную формулу

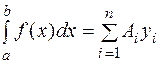, (1)

где

Если пределы интегрирования являются узлами интерполирования, то квадратурная формула называется формулой замкнутого типа, в противном случае – формулой открытого типа.

Получим явные выражения для .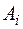

,

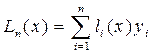где

Обозначим 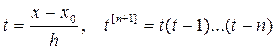, тогда выражение для полинома Лагранжа примет вид

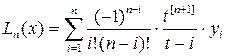. (2)

Подставив в (1) выражение для полинома Лагранжа (2) получим

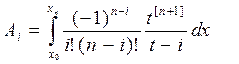. (3)

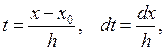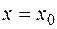
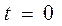Введем замену при , при 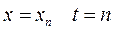, тогда выражение (3) примет вид

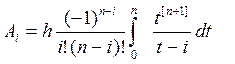(4)

Если учесть, что 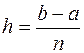и ввести коэффициенты

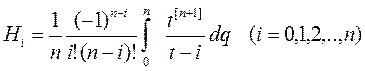, (5)

которые называются коэффициентами Котеса, то получим 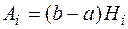и квадратурная формула примет вид

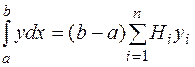(6)

где .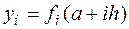

Для коэффициентов Котеса должны выполняться следующие соотношения:

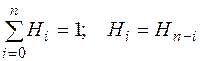(7)