Закон Био – Савара – Лапласа был установлен экспериментально Жаном Батистом Био и Феликсом Саваром в 1820 году. Лаплас придал ему математическую формулировку в виде количественной связи между индукцией магнитного поля в некоторой точке пространства и порождающим ее элементом тока.
Био и Савар экспериментально исследовали магнитные поля, порождаемые токами, текущими по тонким проводникам различной формы. Полученный ими экспериментальный материал теоретически анализировал Лаплас. В основе анализа лежал принцип суперпозиции. Лаплас считал, что в каждом случае Био и Савар наблюдали поле, образованное всеми элементами конкретного проводника с током, то есть
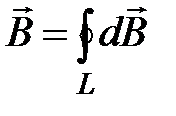 , (7.7)
, (7.7)
где 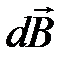 – индукция магнитного поля, создаваемого в данной точке пространства элементом dl замкнутого контура L с током J. Ясно, что выражение (7.7) является обобщением формулы (7.6).
– индукция магнитного поля, создаваемого в данной точке пространства элементом dl замкнутого контура L с током J. Ясно, что выражение (7.7) является обобщением формулы (7.6).
В итоге Лаплас нашел формулу, связывающую 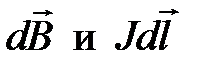 , такую, что после их подстановки в (7.7) и интегрирования получались результаты, совпадающие с опытными данными Био и Савара. Эта формула и получила название закона Био – Савара – Лапласа. В СИ закон Био – Савара –Лапласа имеет вид:
, такую, что после их подстановки в (7.7) и интегрирования получались результаты, совпадающие с опытными данными Био и Савара. Эта формула и получила название закона Био – Савара – Лапласа. В СИ закон Био – Савара –Лапласа имеет вид:
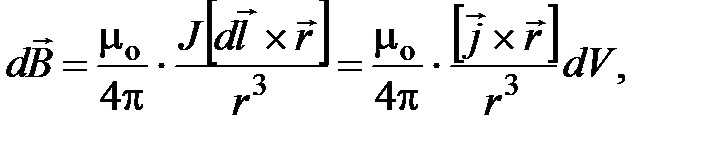 | (7.8) |
где mо=4p∙10–7 Тл∙м/А – магнитная постоянная, характерная для СИ, J – ток в проводнике, 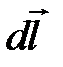 имеет такой же смысл, как и в законе Ампера (7.3), dV – объем трубки тока длиной dl, площадью поперечного сечения dS и плотностью тока
имеет такой же смысл, как и в законе Ампера (7.3), dV – объем трубки тока длиной dl, площадью поперечного сечения dS и плотностью тока  такой, что
такой, что 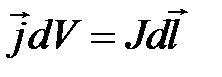 ,
, 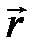 – радиус-вектор, проведенный из элемента
– радиус-вектор, проведенный из элемента 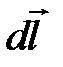 проводника в точку А пространства, где определяется магнитное поле (рис. 7.2).
проводника в точку А пространства, где определяется магнитное поле (рис. 7.2).
Подставляя (7.8) в (7.7), можно найти магнитное поле, создаваемое тонкими проводниками различной формы, то есть 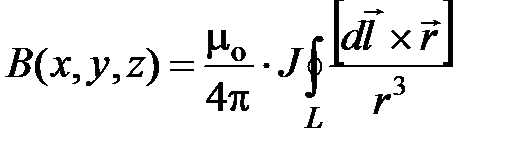 | . |
Магнитное поле длинного прямого провода с током. Пусть по тонкому прямому проводу очень большой длины течет ток J (рис. 7.3). Необходимо вычислить магнитное поле в точке А, расположенной на расстоянии b от провода. Из рис. 7.3 следует, что при выбранном направлении тока все элементы проводника будут создавать в рассматриваемой точке пространства магнитные поля с одинаковым направлением (за плоскость чертежа). Поэтому при использовании формулы (7.9) вместо векторного сложения достаточно применить алгебраическое сложение индукций полей, Рис. 7.3. К расчету магнитного поля, создаваемого прямым длинным проводником с током. Вектор 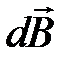 создается элементом создается элементом 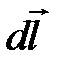 проводника с током J создаваемых всеми элементами проводника с током. Из (7.8) следует, что элемент проводника с током создает в точке А элементарную индукцию магнитного поля, величина которой равна проводника с током J создаваемых всеми элементами проводника с током. Из (7.8) следует, что элемент проводника с током создает в точке А элементарную индукцию магнитного поля, величина которой равна 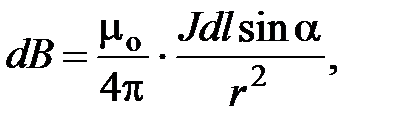 где α – угол между направлением где α – угол между направлением 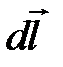 и направлением и направлением 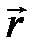 . Из рис. 7.3 видно, что . Из рис. 7.3 видно, что 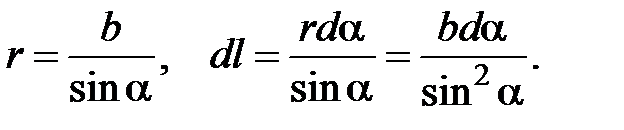 Поэтому Поэтому 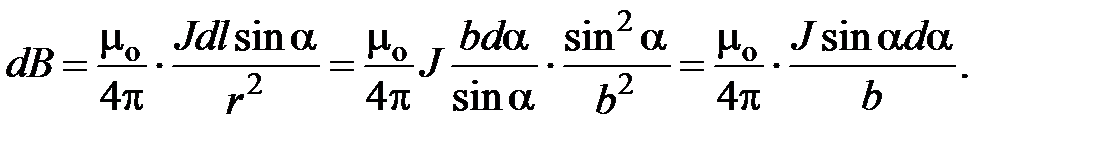 (7.10) Для прямого проводника бесконечной длины точка А с концов проводника будет видна под углом α=0 с его нижнего конца и α=π с его верхнего конца. Поэтому (7.10) Для прямого проводника бесконечной длины точка А с концов проводника будет видна под углом α=0 с его нижнего конца и α=π с его верхнего конца. Поэтому 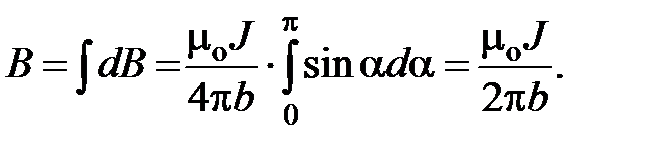 | 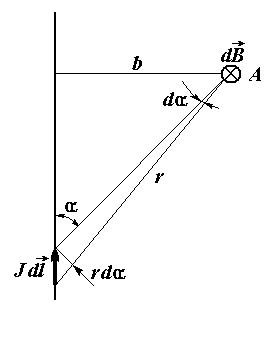 |
Индукции магнитного поля, создаваемого элементом тока, определяется по формуле: 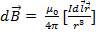 .
.
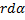 |
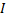 |
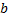 |
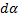 |
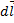 |
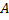 |
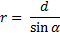 |
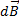 |
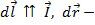 радиус-вектор проведённый из точки
радиус-вектор проведённый из точки к элементу тока, 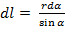 .
. 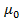 - магнитная постоянная.
- магнитная постоянная.
1. Бесконечный прямой ток
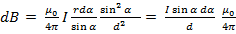
Теперь проинтегрируем 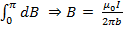
2. Конечный проводной ток
Проинтегрируем 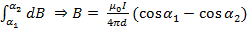
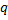 |
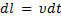 |
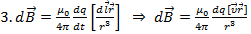
Если заряд конечный, то 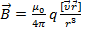 -магнитное поле
-магнитное поле
движущегося заряда.
 2015-01-21
2015-01-21 2478
2478