Применение преобразования Лапласа в задачах теории автоматического регулирования

Исследование АСР с помощью их математических моделей заключается в решении дифференциальных уравнений и анализе получаемых результатов. Процесс решения уравнений можно существенно упростить, если воспользоваться преобразованием Лапласа. Оно позволяет свести процесс решения дифференциального уравнения к решению алгебраического уравнения и к использованию вместо ряда операций стандартных таблиц. Применение преобразования Лапласа аналогично логарифмированию.

Так, если необходимо возвести число a в какую-либо степень n, то отыскание результата 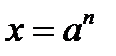с помощью логарифмирования включает известные шаги:

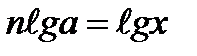, (11.1)

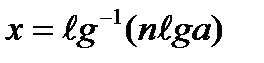, (11.2)

которые выполняются с помощью таблиц логарифмов.

Таким образом сложная операция возведения в степень сводится к более простой – умножению, а при умножении «больших» (астрономических) цифр – к сложению их логарифмов, что существенно снижает риск ошибиться.

Сегодня при использовании вычислительной техники в расчетах вероятность ошибки сведена к нулю, но идея преобразований остается востребованной.

Так, в преобразовании Лапласа производится операция перехода от функций времени f(t) (оригиналов) к функциям F(p) (изображениям) комплексной переменной p по формуле

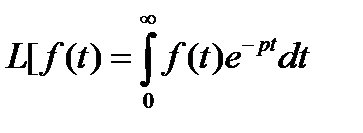, (11.3)

где 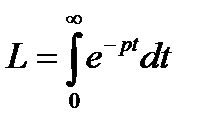– символ прямого преобразования.

Данный переход выполняется на практике с помощью табл. 11.1. После определения неизвестного в пространстве изображений осуществляют с помощью табл.11.1 обратное преобразование и получают искомый результат.

Символически обратное преобразование записывается следующим образом:

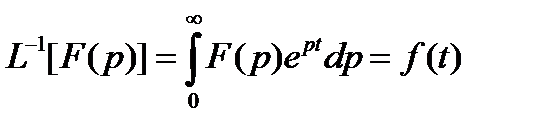. (11.4)

Преобразование Лапласа относится к линейным преобразованиям и имеет следующие свойства:

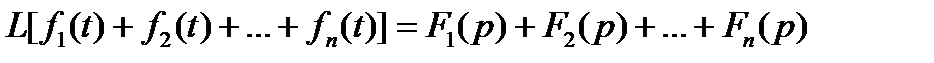, (11.5)

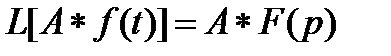, (116)

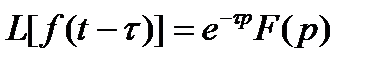, (11.7)

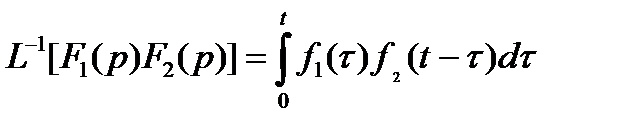. (11.8)

Рассмотрим на примере использование преобразования Лапласа. Пусть имеем дифференциальное уравнение, описывающее процессы в RC-цепи, показанной на рис. 11.1, а.

Получим уравнение цепи

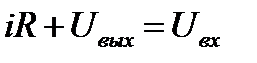, (11.9)

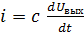, (11.10)

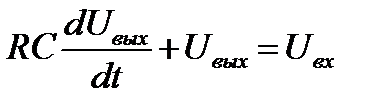(11.11)

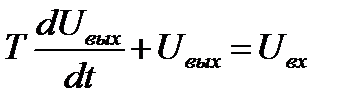, (11.12)

где T = RC, R – сопротивление, C – ёмкость, 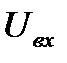и 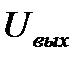– соответственно входное и выходное напряжение цепи.

Найти изменение 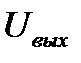(t)при 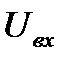(t)= 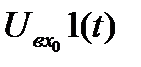и начальном условии
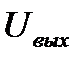(0)= 0.

Используя преобразование Лапласа, получим:

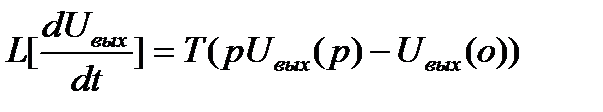, (11.13)

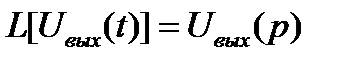, (11.14)

R

U_{вх C} U_вых

а

б

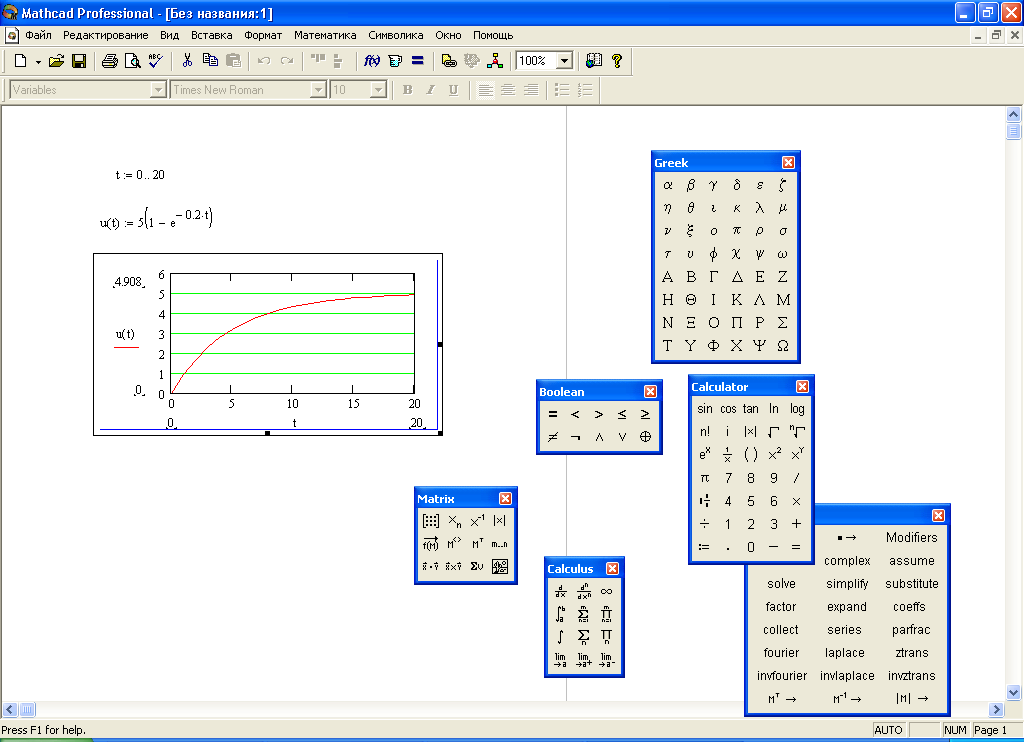
Рис.11.1. RC – цепи

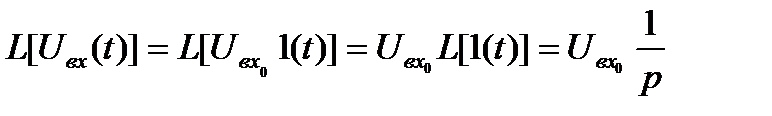, (11.15)

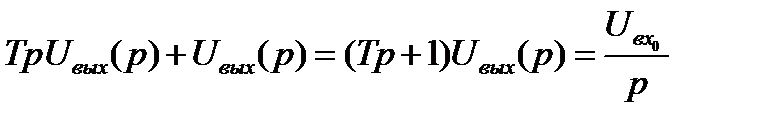. (11.16)

Отсюда находим изображение неизвестной функции:

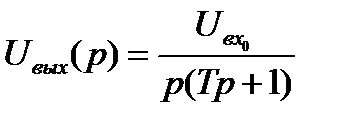. (11.17)

Определим 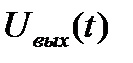с помощью обратного преобразования

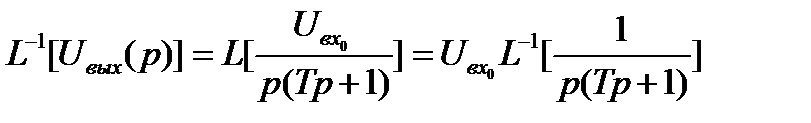. (11.18)

В табл. 11.1 имеем 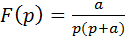. Приведём выражение 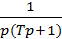к табличному виду, разделив числитель на Т. Тогда получим:

U _вых(t) = 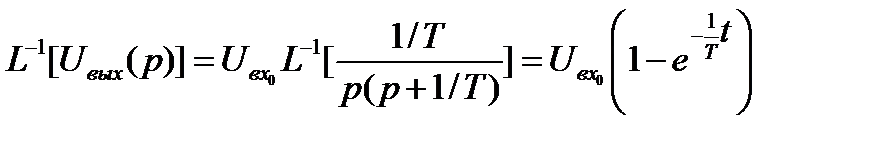(11.19)

График U _вых(t) для U _вх0 =5 и T=5 представлен на рис.11.1,б.

Рассмотрим возможности применения при расчётах теоремы Лапласа о начальном и конечном значениях функции. Математическая запись их соответственно будет:

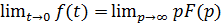(11.20)

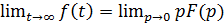(11.21)

Пользуясь данными теоремами, можно существенно сократить количество математических расчётов без отыскания выражения самой функции, если необходимо найти лишь значение искомой функции в начальный или конечный моменты времени.

Так, например, в случае RC-цепи значение U _вых(t) по окончании в ней процессов можно найти с использованием выражения (11.19):

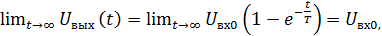(11.22)

проделав предварительно все операции с применением преобразования Лапласа.

Однако ту же задачу с использованием предельной теоремы Лапласа о конечном значении можно решить быстрее, с большей возможностью не совершить ошибок при нахождении результата

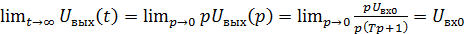(11.23)

При использовании обратного преобразования Лапласа возможны случаи, когда в таблицах нет требуемых функций. Тогда необходимо представить исходную функцию как совокупность простейших, имеющихся в таблице 11.1.

Рассмотрим пример.

Имеем

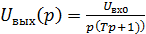. (11.24)

Разложим это выражение на простейшие:

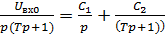. (11.25)

Этот метод носит название метода неопределённых коэффициентов. Коэффициенты C₁ и C₂ неизвестны. Найдём их значения, при которых правая часть выражения будет равна левой. Приводя правую часть уравнения (11.25) к общему знаменателю, получим, что равенство справедливо, когда равны и числители и знаменатели в левой и правой частях. Отсюда следует, что

U_вх0= C₁(Tp+1) + C₂p. (11.26)

Преобразование Лапласа Таблица 11.1.

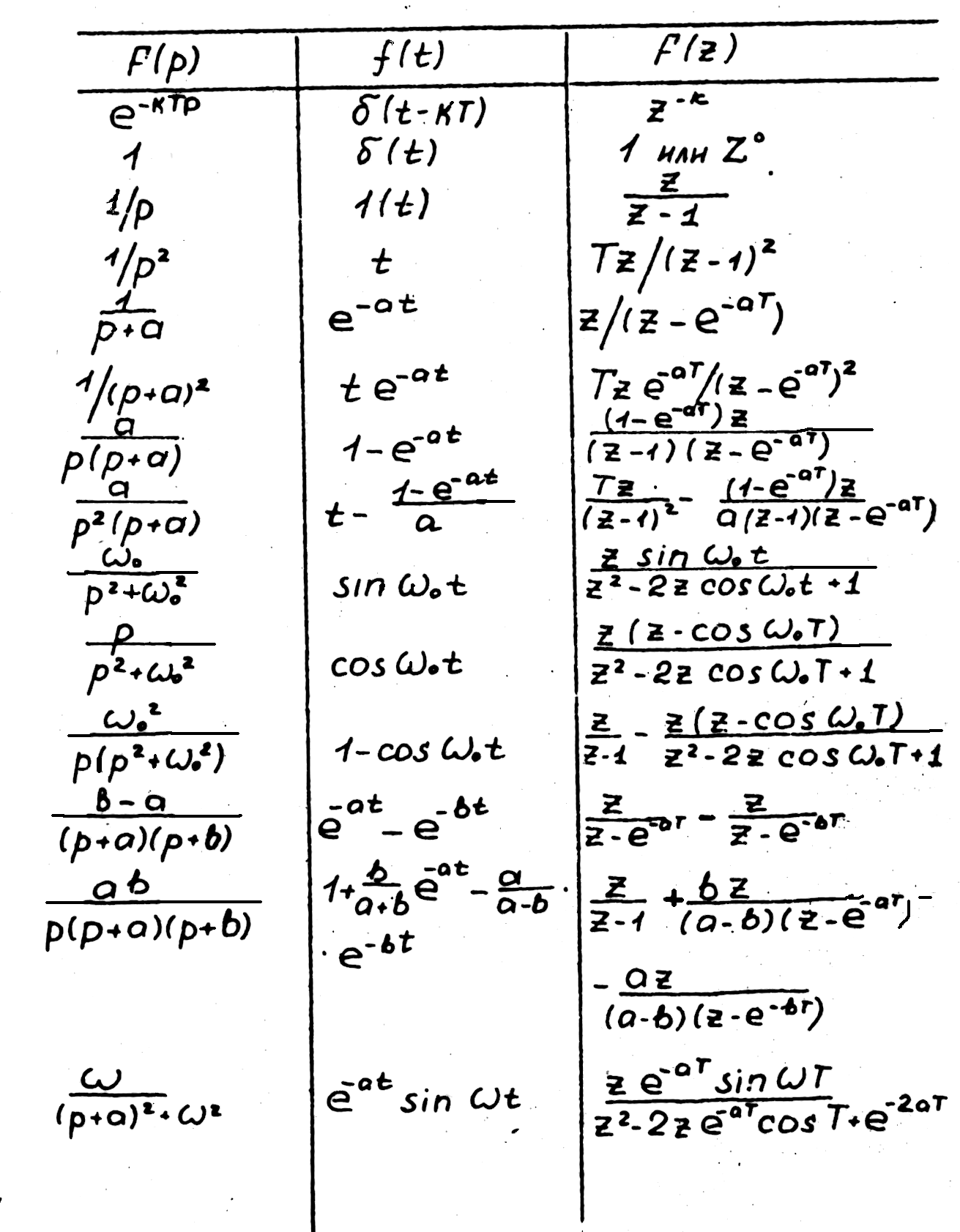
Приравнивая члены при одинаковых степенях p в левой и правой частях (11.26), получим:

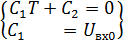(11.27)

откуда C₁ = U_вх0 и C₂ = - U_вх0T.

С учётом найденных значений перепишем уравнение (11.25)

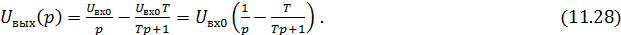Найдём искомую функцию, пользуясь таблицей Лапласа для каждого из слагаемых

U_вых (t) = U_вх0 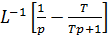= U_вх0 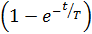. (11.29)