Что такое абстрактная алгебра?

Общая алгебра (также абстрактная алгебра, высшая алгебра) — раздел математики, изучающий алгебраические системы (также иногда называемые алгебраическими структурами), такие как группы, кольца, поля, частично упорядоченные множества, решётки, а также отображения между такими структурами.

Примерами алгебраических структур с бинарной операцией являются:

полугруппы, моноиды, группы, квазигруппы, полурешётки,

две бинарных операции — в кольцах, почти-кольцах, полях, решётках.

Более сложными примерами алгебраических структур являются модули над кольцами, векторные пространства, ассоциативные алгебры, алгебры Ли.

Особо изучаются тернарные алгебры, полиадические алгебры (например, полиадические группы), многосортные алгебры.

Для изучения структур используются общие методы и сходные понятия: для отображения между структурами вводятся понятия:

гомоморфизмов, изоморфизмов, автоморфизмов, для изучения внутреннего строения вводятся подсистемы (подгруппы, подкольца, подрешётки) и факторсистемы (факторгруппы, факторкольца, факторрешётки). Векторные пространства и линейные отображения между ними изучаются в разделе под названием линейная алгебра. Алгебраические уравнения высших порядков от одной переменной, а также, более общо, свойства групп автоморфизмов различных алгебраических систем есть предмет теории Галуа.

Наиболее общие для всех этих алгебраических систем свойства формализуются и изучаются специальным разделом общей алгебры — универсальной алгеброй. Теория категорий, также считающаяся разделом общей алгебры, изучает свойства алгебраических структур и соотношений между ними с использованием таких абстракций, как объекты, морфизмы, функторы, которые обобщают соответствующие понятия не только в алгебраических структурах, но и в топологии, логике, теории множеств.

Другое определение. Абстрактная или высшая алгебра - область математики, сосредоточена на изучении свойств аксиоматически внедренных алгебраических структур. В современной научной литературе называется просто алгебра. Признак «абстрактная» подчеркивает, что объектами изучения являются абстрактные структуры, такие как:

группы;

кольца;

поля;

и модули,

в отличие от алгебраических выражений, изучаемых в элементарной «школьной» алгебре.

Преимущество работы с абстрактными математическими понятиями может быть оценено лишь при необходимости рассматривать многочисленные частные примеры.

Что значит построить аксиоматическую теорию данной алгебраической структуры? Это значит вывести логические следствия из её аксиом, отказавшись от всяких других предположений относительно рассматриваемых элементов. Множество, на котором заданы одна или несколько операций, представляет собой алгебраическую структуру.

Аксиоматический метод и понятие алгебраической структуры позволяют математикам исследовать сущность понятия операции, выяснить её свойства, доказать в общем виде теоремы, которые до этого были известны, может быть, лишь в частных случаях.

Например, рассмотрев алгебраические структуры группы, кольца, поля, мы имеем возможность в общем виде исследовать вопросы о выполнимости обратных операций вычитания, деления, о правилах раскрытия скобок, о решении уравнений не только в числовой области, но и для классов вычетов, поворотов плоскости, множеств, функций и других объектов.

Современная алгебра изучает множества, на которых определены одна или несколько операций. При этом совершенно не важно, из каких элементов состоят эти множества, необходимо только, чтобы выполнялись определённые отношения между элементами. Эти отношения задаются с помощью системы требований, составляющих совокупность аксиом. Например, современная математика исследует структуру отношений между объектами.

Понятие алгебры является одним из важнейших в математике. Под алгеброй понимается векторное пространство 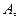в котором задана операция умножения, т.е. каждой паре элементов 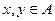сопоставлен элемент 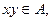который называется их произведением, при этом выполнены обычные законы дистрибутивности. Если в качестве скаляров для векторного пространства берутся вещественные (комплексные) числа, то говорят о вещественной (комплексной) алгебре. Алгебра называется коммутативной, если 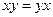для всех 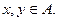Алгебра называется ассоциативной, если 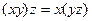, для всех 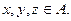Существуют и другие классы алгебр (например, существует неассоциативная алгебра).

1. Ассоциативность сложения и умножения:

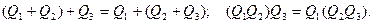
2. Коммутативность: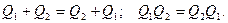

3. Дистрибутивность: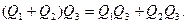

4. Однозначность деления: если 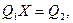то определяется одно и только одно число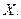

5. «Закон модулей»: если 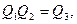то .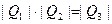

6. Взаимно однозначное соответствие между точками трёхмерного пространства и числами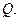

Термин «ассоциативность» ввёл Гамильтон, а «коммутативность» и «дистрибутивность» - Сервуа. Гамильтон ввёл «современное» определение комплексного числа как упорядоченной пары действительных чисел с аксиоматическим заданием операций для этих пар.

Обычная линейная алгебра с основной определяющей её билинейной операцией умножения представляет собой простейший, наиболее симметричный тип общей алгебраической структуры (универсальной алгебры) и отвечает изотропной (как на макро-, так и на микроуровне) геометрии пространства-времени, с возможной особенностью в нуле (в силу выделенности нулевого элемента и отсутствием для него обратного).

Что такое компьютерная алгебра.

Введение

Бывает, что человек обладает знанием, но не умеет пользоваться им. Бывает и так, что владеющий искусством сам не знает его секрета. В царстве Вэй жил человек, умевший хорошо считать. Перед смертью он поведал секрет своего искусства сыну. Сын запомнил слова, но не знал, как применить их. Какой-то человек стал его расспрашивать об этом, и он передал ему те слова. И тот человек научился считать не хуже, чем это делал отец.

Ле-цзы, Гл. VIII. Рассказы о совпадениях

Человек может пользоваться только тем, чем он умеет пользовать­ся.

Человек может использовать только то, что он знает, как исполь­зовать

Идрис Шах, 'Сказки дервишей

Was man nich versteht, besitzt man nicht. — Чего человек не пони­мает, то ему не принадлежит.

Johann Wolfgang von Goethe, Maximen und Reflexionen

Nessuna certezza e dove non si po applicare la matematica. — Там, где нельзя применить Mathematica, не может быть никакой досто­верности.

Leonardo da Vinci

They spell it da Vinci and pronounce it da Vinchy. Foreigners always spell better than they pronounce. — Они пишут da Vinci, а про­износят да Винчи. Иностранцы всегда пишут гораздо лучше, чем говорят.

Mark Twain

Описываемая в настоящей лекции система Maple (Mathematica) является си­стемой компьютерной алгебры общего назначения, при помощи ко­торой можно решать любой тип задач, в которых в той или иной форме встречается математика. При этом Maple наряду с Mathematica являет­ся единственной такой high-end системой, которая настолько проста в использовании, что доступна школьникам и студентам младших курсов.

Maple (Mathematica), как и любая система компьютерной алгебры, может изла­гаться с точки зрения

• математика,

• программиста,

• пользователя.

Пользователь интересуется этой системой не с точки зрения принципов ее работы, а как законченным программным продуктом для проведения прак­тических вычислений в конкретной предметной области, скажем, в матема­тике, физике, информатике, технических науках, химии, астрономии, гео­логии, экономике, управлении, проектировании, архитектуре, лингвистике, компьютерной графике, музыке и т.д. При этом он совершенно не обязан понимать ни математических основ работы системы, ни используемых в ней алгоритмов, ни собственно программистских аспектов ее реализации, ее взаимодействия с платформой, операционной системой и другими про­граммами и других подобных вещей. Тем не менее, любой серьезный поль­зователь, который хочет использовать эти системы не просто в качестве редактора формул и большого научного калькулятора (в духе Scientific Workplace или Mathcad), любой грамотный пользователь, который хочет избежать хотя бы наиболее очевидных ошибок и эффективно использовать возможности этих систем, должен понимать хотя бы основные принципы компьютерной алгебры, взаимоотношение математической и вычислитель­ной точек зрения и, в первую очередь, принятые в этих системах стандарт­ные соглашения и специфику используемого ими языка.

Символьные вычисления — это преобразования и работа с математическими равенствами и формулами как с последовательностью символов. Они отличаются от численных расчётов, которые оперируют приближёнными численными значениями, стоящими за математическими выражениями. Системы символьных вычислений (их так же называют системами компьютерной алгебры) могут быть использованы для символьного интегрирования и дифференцирования, подстановки одних выражений в другие, упрощения формул и т. д.

Компьютерная алгебра (в отличие от численных методов) занимается разработкой и реализацией аналитических методов решения математических задач c использованием ПЭВМ и предполагает, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде.

При анализе математической модели результатом могут быть общие и частные аналитические решения сформулированной математической задачи и их интерпретации.

Аналитические решения чаще удаётся получить для наиболее грубых (простых) моделей, реже — для более точных, сложных (нужно использовать численные методы, позволяющие получить частные численные решения многих задач).

Компьютерная алгебра — область математики, лежащая на стыке алгебры и вычислительных методов. Для нее, как и для любой области, лежащей на стыке различных наук, трудно определить четкие границы. Часто говорят, что к компьютерной алгебре относятся вопросы слишком алгебраические, чтобы содержаться в учебниках по вычислительной математике, и слишком вычислительные, чтобы содержаться в учебниках по алгебре. При этом ответ на вопрос о том, относится ли конкретная задача к компьютерной алгебре, часто зависит от склонностей специалиста.

Термин " компьютерная алгебра " возник как синоним терминов "символьные вычисления", "аналитические вычисления", "аналитические преобразования" и т. д. Даже в настоящее время этот термин на французском языке дословно означает "формальные вычисления ".

Причины возникновения

В чем основные отличия символьных вычислений от численных и почему возник термин " компьютерная алгебра "?

Когда мы говорим о вычислительных методах, то считаем, что все вычисления выполняются в поле вещественных или комплексных чисел.

1. В действительности же всякая программа для ЭВМ имеет дело только с конечным набором рациональных чисел, поскольку только такие числа представляются в компьютере. Для записи целого числа отводится обычно 16 или 32 двоичных символа (бита), для вещественного—32 или 64 бита. Это множество не замкнуто относительно арифметических операций, что может выражаться в различных переполнениях, например, при умножении достаточно больших чисел или при делении на маленькое число.

2. Еще более существенной особенностью вычислительной математики является то, что арифметические операции над этими числами, выполняемые компьютером, отличаются от арифметических операций в поле рациональных чисел,— более того, для компьютерных операций не выполняются основные аксиомы поля (ассоциативности, дистрибутивности). Эти особенности компьютерных вычислений оцениваются в терминах погрешности или точности вычислений. Оценка погрешности представляет одну из основных проблем вычислительной математики. Каждую задачу требуется решить с использованием имеющихся ресурсов ЭВМ, за обозримое время, с заданной точностью.

Набор объектов, применяемых в символьных вычислениях, весьма разнообразен, в частности, в них используется значительно большее множество рациональных чисел. Это множество все равно остается конечным, но ограничения на допустимые размеры числа (количество знаков в его записи) связаны обычно с размерами оперативной памяти ЭВМ, что позволяет пользоваться практически любыми рациональными числами, операции над которыми выполняются за приемлемое время. При этом компьютерные операции над рациональными числами совпадают с соответствующими операциями в поле рациональных чисел. Таким образом, снимается одна из основных проблем вычислительных методов — оценка погрешности вычислений.

В компьютерной алгебре вещественные и комплексные числа практически не применяются, зато широко используются алгебраические числа. Алгебраическое число задается своим минимальным многочленом, а иногда для его задания требуется указать интервал на прямой или область в комплексной плоскости, где содержится единственный корень данного многочлена. Многочлены играют в символьных вычислениях исключительно важную роль. На использовании полиномиальной арифметики основаны теоретические методы аналитической механики, они применяются во многих областях математики, физики и других наук. Кроме того, в компьютерной алгебре рассматриваются такие объекты, как дифференциальные поля (функциональные поля), допускающие показательные, логарифмические, тригонометрические функции, матричные кольца (элементы матрицы принадлежат кольцам достаточно общего вида) и другие. Даже при арифметических операциях над такими объектами происходит разбухание информации, и для записи промежуточных результатов вычислений требуется значительный объем памяти ЭВМ.

Ограничения на алгоритмы решаемых компьютерной алгеброй задач накладываются имеющимися ресурсами ЭВМ и обозримостью времени счета. Однако ограничения по времени счета и по используемой памяти в символьных вычислениях существенно более обременительны, чем в вычислительных методах.

В научных исследованиях и технических расчетах специалистам приходится гораздо больше заниматься преобразованиями формул, чем собственно численным счетом. Тем не менее, с появлением ЭВМ основное внимание уделялось автоматизации численных вычислений, хотя ЭВМ начали применяться для решения таких задач символьных преобразований, как, например, символьное дифференцирование, еще в 50-х годах прошлого века. Активная разработка систем компьютерной алгебры началась в конце 60-х годов. С тех пор создано значительное количество различных систем, получивших различную степень распространения; некоторые системы продолжают развиваться, другие отмирают, и постоянно появляются новые.