Разложение автоматов и расщепляемый автомат

Пусть H _k (S _i) обозначает множество всех состояний автомата М, соединенных с состояниями S _i = { σ i ₁, σ i ₂,..., σ i _r} посредством k или меньшего числа дуг, причем направление дуг несущественно. В частности, H₀(S _i) = S _i. Множество H₁S(_i) есть объединение S _i - состояний, расположенных в строках σ i ₁, σ i ₂,..., σ i _r s _v+1 -подтаблицы таблицы переходов автомата М, и состояний основного столбца таблицы переходов, соответствующих строкам s _v+1 -подтаблицы, в которых есть какое-либо состояние из множества S _i. С другой стороны, Н₁ (S _i) можно составить путем просмотра графа переходов автомата М. Если задано H_k-l(S _i), k≥1, то H _k (S _i) может быть определено из соотношения

H _k (S _i) = H₁(H _k-l (S _i)). (2.10)

Если H _k (S _i) = H _k-1 (S _i). то H _k+u (S _i) = H _k-l (S _i) для всех неотрицательных целых u и, следовательно, H _k-l (S _i) составляет множество всех состояний, связанных с S _i цепью ребер[12] любой длины. Определение этого множества, обозначаемого просто H(S _i), может быть теперь описано при помощи следующего алгоритма.

Алгоритм 2.2. Дано S _i, требуется найти H(S _i). (1) Пусть H₀(S _i) = S _i. Полагаем k =1. (2) Определяем H _k (S _i) = H₁(H _k-l (S _i)). (3) (а) Если H _k (S _i) ≠ H _k-1 (S _i), то увеличиваем k на единицу и возвращаемся к (2). (б) Если H _k (S _i) = H _k-l (S _i). то H _k (S _i) = H(S _i).

При помощи аргументов, аналогичных тем, которые были использованы для алгоритма 2.1, можно показать, что алгоритм 2.2 требует не более n - r итераций пункта 2, где n - мощность множества состояний S автомата М, а r - мощность множества S _i. Таблица 2.6 иллюстрирует применение этого алгоритма для автомата ЛЗ, изображенного на рис. 2.5 для S _i = {1, 4}, H(1, 4) = {1, 2, 4, 5, 7, 8}.

Автомат или подавтомат, который содержит два или большее число изолированных подавтоматов, будем называть разложимым. Ранее упоминалось, что если S _i содержит единственное состояние σ _i, то H(σ _i) составляет множество всех состояний, соединенных с σ _i посредством цепей ребер любой длины. Следовательно, если H(σ _i) ≠ S, то H(σ_i) составляет неразложимый изолированный подавтомат автомата М. Если H(σ _i) = S, то можно заключить, что автомат М неразложим. Теперь можно описать метод получения максимального разложения автомата, т. е. метод разложения автомата на максимально возможное число изолированных

подавтоматов.

Алгоритм 2.3. Определение максимального разложения заданного автомата М с множеством состояний S.

(1) Пусть S₁=S. Пологаем k =1. (2) Выбираем любое состояние из S _k, например σi _k, и определяем H(σi_k). Множество H(σi_k) – множество состояний k -го изолированного подавтомата автомата M. (3) (а) Если H(σi₁) 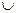H(σi₂) 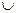... 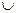H(σi_k) ≠ S, то полагаем, что S _k+1 содержит состояния множества S, не содержащиеся H(σi₁) 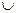H(σi₂) 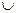... 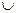H(σi_k). Увеличиваем k на единицу и возвращаемся к (2). (б) Если H(σi₁) 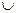H(σi₂) 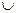... 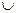H(σi_k) = S, то подавтоматы, определяемые множествами H(σi₁), H(σi₂), H(σi_k) представляют максимальное разложение автомата M. В частности, если H(σi₁) = S, то автомат M неразложим.

Алгоритм 2.3, конечно, не обязателен, если автомат задан в виде графа. Однако он нужен, когда максимальное разложение надо провести без использования графа, например при помощи цифровой вычислительной машины.

Два или большее число автоматов называются сравнимыми, если они имеют одинаковые входные алфавиты. Пусть М₁, M₂,..., M _N — сравнимые автоматы, представляющие N различных систем, и пусть M — автомат, который состоит из изолированных подавтоматов М₁, M₂,..., M _N. М называется расщепляемым автоматом автоматов М₁, M₂,..., M _N и обозначается так: ∆(М₁, M₂,..., M _N). При заданных таблицах переходов М₁, M₂,..., M _N таблица переходов ∆(М₁, M₂,..., M _N) может быть построена следующим образом. (1) Переобозначим состояния автомата M _i, если необходимо, так, чтобы не было в одном и том же автомате или в двух различных автоматах двух состояний, обозначенных одинаково. (2) Запишем строки всех N таблиц последовательно в одну общую таблицу; эта таблица является таблицей переходов автомата ∆(М₁, M₂,..., M _N). Если M _i определены графами, то граф переходов ∆(М₁, M₂,..., M _N) является просто объединением всех отдельных графов, состояния которых могут быть перенумерованы в случае необходимости в соответствии с указанным выше правилом.

Понятно, что расщепляемый автомат ∆(М₁, M₂,..., M _N) и, следовательно, каждый автомат, содержащий ряд подавтоматов, определенных так же, как М₁, M₂,..., M _N, может рассматриваться как «система», которая есть автомат M₁ или

автомат М₂ или автомат M _N. Эта интерпретация основывается на том факте, что если ∆(М₁, M₂,..., M _N) находится в состоянии σ _u, принадлежащем подавтомату M _i, то ∆(М₁, M₂,..., M _N) никогда не может перейти в какое - либо состояние подавтомата M _j, где j ≠ i, так как M _i и M _j — два изолированных подавтомата. Поведение автомата ∆(М₁, M₂,..., M _N), находящегося в состоянии σ _u, совпадает поэтому с поведением автомата M _i, находящегося в состоянии σ _u. Следовательно, автомат ∆(М₁, M₂,..., M _N) может быть представлен автоматом М₁, или автоматом M₂ или автоматом M _N, в зависимости от начального состояния.

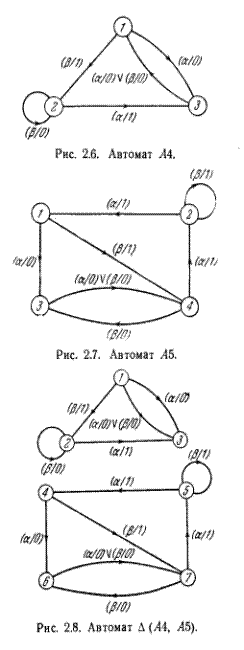
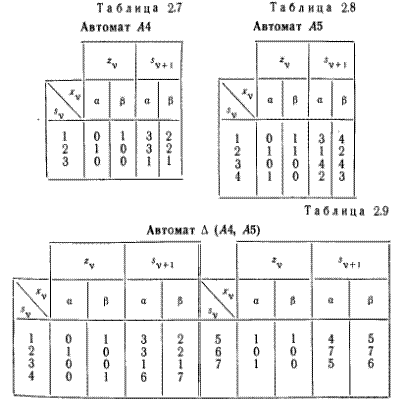
В качестве примера рис. 2.6 и таблица 2.7 представляют автомат A4, а рис. 2.7 и таблица 2.8—автомат A5. Расщепляемый автомат, составленный из автоматов A4 и A5, ∆ (A4, A5), представлен на рис. 2.8 и в таблице 2.9.

2.8. Матрица переходов [13]

Матрицы переходов являются математической копией графов переходов; они дают возможность формализовать ряд операций, которые на графе переходов могут быть выполнены визуально. Матрицы переходов поэтому имеют преимущества в тех случаях, когда эти операции не могут быть выполнены человеком-исследователем и, следовательно, не могут быть выполнены визуально или когда граф переходов настолько сложен, что использование визуальной методики бесполезно.

Для автомата М, имеющего n состояний, матрица переходов состоит из n. строк и n столбцов и обозначается [М]. Пусть {σ₁, σ₂,.:., σ_n}—множество состояний автомата М и пусть b _ij обозначает дугу графа переходов автомата М, направленную от σ _i к σ _j. Элемент (i, j) (т. е. содержимое клетки, расположенной на пересечении i-й строки и j-го столбца матрицы [М] обозначается е _ij и определяется так:

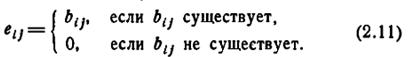
Для ясности обычно обозначение k -го состояния σ _k приписывают k-й строке и k-му столбцу и называют их «строка σ _k» и «столбец σ _k» соответственно. Выражение (2.12) изображает матрицу переходов автомата А1, заданного в виде графа на рис. 2.2.

Если р — мощность входного алфавита автомата М, то каждая строка в [М] должна содержать точно р пар вход-выход, причем каждая пара имеет входной символ, отличный от входного символа любой другой пары. Дуги, заходящие в состояние σ _k, представляются недиагональными элементами[14] столбца σ _k; дуги, исходящие из состояния σ _k, представляются недиагональными элементами строки σ _k; петля состояния σ _k представляется диагональным элементом в строке σ _k или

столбце σ _k. Следовательно, если σ _k — переходящее состояние, то все недиагональные элементы в столбце σ _k (но не в строке σ _k) равны нулю; если σ _k —тупиковое состояние, то все недиагональные элементы в строке σ _k (но не в столбце σ _k) равны нулю; если σ _k —изолированное состояние, то все недиагональные элементы в строке σ _k и столбце σ _k равны нулю.

Если S _i = {σ i ₁, σ i ₂,..., σ i _r}, то определенное в § 2.6 множество G ₁ (S _i) представляет собой объединение S _i и обозначений столбцов, в которых элементы, принадлежащие строкам σ i ₁, σ i ₂,..., σ i _r, не равны нулю. Определенное в § 2.7 множество H_I(S _i) представляет собой объединение S _i обозначений столбцов, в которых элементы, принадлежащие строкам σ i ₁, σ i ₂,..., σ i _r, не равны нулю, и обозначений строк, в которых элементы, принадлежащие столбцам σ i ₁, σ i ₂,..., σ i _r, не равны нулю. Например, из матрицы [Al] ясно видно, что для автомата A1 G₁(l, 2) = {1, 2, 3} и Н₁(4, 5)={1, 3, 4, 5}. Таким образом, ясно, что матрица переходов является удобным инструментом для выполнения алгоритмов 2.1, 2.2 и 2.3.

Для того чтобы определить, составляет ли множество S(σ i ₁, σ i ₂,..., σ i _r) преходящий, тупиковый или изолированный подавтомат автомата М, надо строки и столбцы матрицы [М] переставить так, чтобы строки и столбцы σ i ₁, σ i ₂,..., σ i _r заняли соседние положения, начиная с первой строки и первого столбца соответственно. Как показано в (2.13), эта перестановка делит матрицу [М] на четыре подматрицы [М₁₁], [М₁₂], [M₂₁], [М₂₂], причем строками и столбцами [М₁₁] являются строки и столбцы σ i ₁, σ i ₂,..., σ i _r

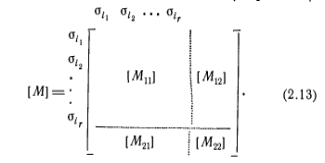
Обозначая матрицу, все элементы которой равны нулю, через [0], можно сделать вывод, что S _i составляет преходящий подавтомат, если [M₂₁] = [0], а [М₁₂] ≠ 0, тупиковый подавтомат, если [М₁₂] = [0], а [M₂₁] ≠ 0, и изолированный подавтомат, если [М₁₂] = [М₂₁] = [0]. В (2.14) представлена матрица переходов автомата A3, изображенного на рис. 2.5, в которой строки и столбцы переставлены так, чтобы выделить тупиковый подавтомат {1, 4, 7}, преходящий подавтомат {2, 5, 8} и изолированный подавтомат {3, 6, 9}.

Если S_i составляет тупиковый или изолированный подавтомат, то [M₁₂] = [0] и, следовательно, каждая строка в [М₁₁] содержит все р пар вход-выход, где р — мощность входного алфавита. Удалив [M₁₂], [M₂₁] и [М₂₂] из [М], получим матрицу [М₁₁] размером r 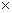r, которую можно трактовать как матрицу, представляющую независимый автомат М₁₁ с r состояниями, имеющий тот же входной алфавит, что и М. Отсюда следует то же заключение, которое было получено в § 2.6: если автомат находится в состоянии, принадлежащем тупиковому или изолированному подавтомату, то все состояния, которые не принадлежат этому подавтомату, и все дуги, исходящие из этих состояний, могут быть исключены.