ЛЕКЦИЯ 1. МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ.
Цель лекции: Дать основные представления о методах матричной алгебры и научить студентов выполнять элементарные алгебраические преобразования матриц и определителей.
Ключевые слова: определитель, матрица, разложение Лапласа, обратная матрица, ранг матриц.
План лекции
1. Понятия матрицы и их виды.
2. Действия над матрицами и их свойства.
3. Понятие определителя n-го порядка. Свойства определителей.
4. Вычисления определителей n-го порядка. Теорема Лапласа.
5. Обратная матрица.
6. Ранг матрицы.
1.Понятия матрицы и их виды.
Определение 1. Матрицей размерности (порядка) mxn называется прямоугольная таблица чисел:
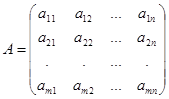 . (1)
. (1)
Числа аij называются элементами матрицы, где i – означает номер строки, j – означает номер столбца. Матрицы обозначаются заглавными буквами А,В,С, …, элементы матрицы – строчными буквами 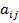 ,
, 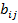 .. Матрицу (1) записывается в компактном виде
.. Матрицу (1) записывается в компактном виде 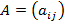 ,
, 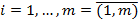 ,
, 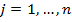 =
= 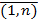 .
.
Матрица называется квадратной n-го порядка, если число строк равно числу столбцов.
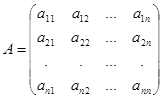 (2)
(2)
Определение 2. Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем ее левый верхний угол с правым нижним, т.е. совокупность элементов 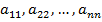 , называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним - побочной диагональю.
, называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним - побочной диагональю.
Квадратная матрица порядка n называется диагональной, если 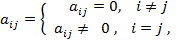 т.е. ненулевыми могут быть только элементы главной диагонали
т.е. ненулевыми могут быть только элементы главной диагонали
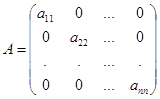 (3)
(3)
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной матрицей
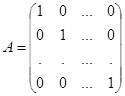 (4)
(4)
Квадратная матрица порядка n называется:
a) Верхней треугольной матрицей, если 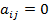 для всех
для всех 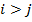 , т.е. сверху главной диагонали ненулевые элементы
, т.е. сверху главной диагонали ненулевые элементы
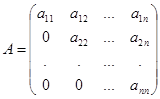
b) Нижней треугольной матрицей, если 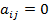 для всех
для всех 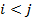 , т.е. снизу главной диагонали ненулевые элементы
, т.е. снизу главной диагонали ненулевые элементы
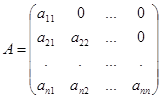
Матрица, все элементы которой равны нулю, называется нулевой матрицей.
Матрица размера 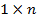 , состоящая из одной строки, называется матрицей-строкой.
, состоящая из одной строки, называется матрицей-строкой.
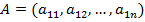 .
.
Матрица размера 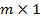 , состоящая из одного столбца, называется матрицей-столбцом.
, состоящая из одного столбца, называется матрицей-столбцом.
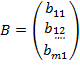
Если в матрице А переставить строки и столбцы местами, то получим новую матрицу АТ транспонированную к матрице А:
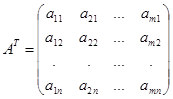
2. Действия над матрицами и их свойства.
Определение. Две матрицы A и B называются равными (A=B), если они имеют одинаковые размеры и их соответствующие элементы равны: 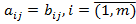 ,
, 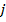 =
= 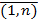
a) Cуммой (разностью) матриц A и B одинакового размера называется матрица C того же размера, каждый элемент которой равен сумме (разности) соответствующих элементов матриц A и B, т.е.
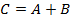 , если
, если 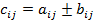 ,
, 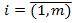 ,
, 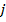 =
= 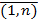 .
.
b) Чтобы умножить матрицу A на число 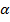 , нужно каждый элемент данной матрицы умножить на это число.
, нужно каждый элемент данной матрицы умножить на это число.
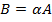 , если
, если 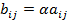 ,
, 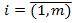 ,
, 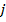 =
= 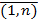 .
.
c) Умножение матрицы A, размерности 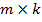 , на матрицу B, размерности
, на матрицу B, размерности 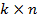 , определено, когда число столбцов первой матрицы равно числу строк второй. Тогдапроизведением матрицы А на матрицу В называется такая матрица С, каждый элемент
, определено, когда число столбцов первой матрицы равно числу строк второй. Тогдапроизведением матрицы А на матрицу В называется такая матрица С, каждый элемент 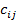 сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В. Матрица С имеет столько строк, сколько матрица А, и столько столбцов, сколько матрица В.
сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В. Матрица С имеет столько строк, сколько матрица А, и столько столбцов, сколько матрица В.
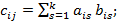
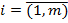 ,
, 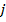 =
= 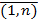
Правило умножения матриц называют «строка на столбец».
Свойства операций суммирования матриц, произведения матрицы на число и произведения матриц
1) 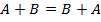 ,
,
2) 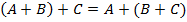 ,
,
3) 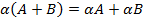 ,
,
4) 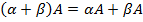 ,
,
5) 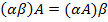 ,
,
6) 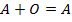 , где O - нулевая матрица,
, где O - нулевая матрица,
7) 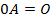 ,
,
8) 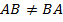
9) (AB) C = A (BC),
10) 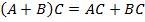 ,
,
11) 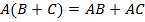 ,
,
12) 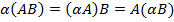
13) 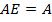 , где
, где 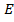 - единичная матрица.
- единичная матрица.
3. Понятие определителя n-го порядка.Свойства определителей.
Определитель n-го порядка записывается в виде квадратной таблицы, содержащей n строк и n столбцов:
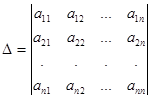
Определение. Определителем матрицы A n-го порядка называется алгебраическая сумма n! произведений n-го порядка элементов этой матрицы, причем в каждое произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы.
Основные свойства определителей n - го порядка.
1. При замене строк столбцами значение определителя не меняется.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Если все элементы какой-нибудь строки (столбца) определителя равны нулю, то определитель равен нулю.
4. Если определитель имеет две одинаковые или пропорциональные строки (столбца), то такой определитель равен нулю.
5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя.
6. Значение определителя не изменится, если к элементам какой-нибудь строки (столбца) добавить элементы другой строки (столбца), умноженные на одно и то же число.
7. Если элементы какой-нибудь строки (столбца) являются линейной комбинацией соответствующих элементов двух (или нескольких) других строк (столбцов), то такой определитель равен нулю.
Методы вычисления определителей 2-го и 3-го порядков.
Величину 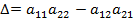 называют определителем (детерминантом) второго порядка и обозначают
называют определителем (детерминантом) второго порядка и обозначают
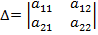 . Таким образом,
. Таким образом,
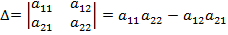 .
.
Определителем третьего порядка называют величину
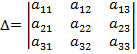 =
= 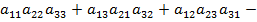
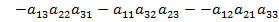 .
.
Эта формула называется правилом Сарруса (правило «треугольников») для вычисления определителей 3-го порядка. Для лучшего запоминания формулы можно составить таблицу Сарруса, добавив к определителю первый и второй столбцы. Тогда все члены будут представлять собой произведение элементов по диагоналям.
4. Вычисления определителей n-го порядка. Теорема Лапласа.
Вычисление определителей более высоких порядков непосредственно весьма сложно, поэтому для их вычисления используют свойства определителей, а также теорему Лапласа, позволяющую понижать порядок данного определителя.
Пусть дан определитель:
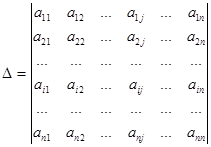
Вычеркнем в этом определителе i-ую строку и j-ый столбец, на пересечении которых находится элемент аij. Тогда получим определитель Mij (n-1)–го порядка, который называют минором элемента аij.
Алгебраическим дополнением Аij элемента аij называют минор этого элемента, взятый со знаком (+), если сумма индексов i+j – четное число, и со знаком (-), если эта сумма – число нечетное, т.е.
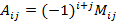
Теорема Лапласа. Определительквадратной матрицыравен с умме произведений элементов любой строки (или столбца) на их соответствующие алгебраические дополнения, т.е.
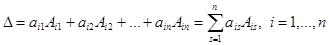
(разложение по элементам i -ой строки) или
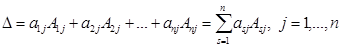
(разложение по j -го столбца).
Эта теорема дает возможность разложить определитель по элементам какой-нибудь строки или столбца и свести его вычисление к вычислению определителей более низкого порядка. При этом вычисление определителя значительно упрощается, если среди элементов некоторой строки (столбца) имеются нули.
Квадратная матрица n-го порядка называется вырожденной (особенной), если определитель n-го порядка, составленный из ее элементов, равен нулю, т.е. 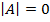 . В противном случае, матрица называется невырожденной (неособенной).
. В противном случае, матрица называется невырожденной (неособенной).
5. Обратная матрица.
Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную получается единичная матрица, т.е.
А·А-1 = А-1·А = Е
Обратная матрица вычисляется по формуле
А-1 = 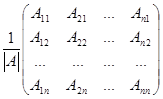 ,
,
где Аij – алгебраические дополнения к элементам аij матрицы А.
Обратная матрица А-1 существует (и единственна) тогда и только тогда, когда исходная матрица А невырожденная, т.е. 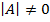 .
.
Свойства обратных матриц.
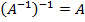 ;
; 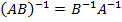 ;
; 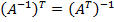 .
.
Ранг матрицы.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
Ранг матрицы А обозначают rang А или r(A). Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Пример. Вычислить ранг матрицы 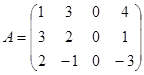
Вычислим все миноры 3-го порядка.
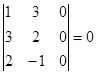 ;
; 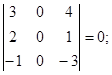
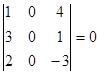 ;
; 
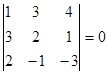
Теперь вычислим минор 2-го порядка 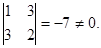
Так как существует ненулевой минор второго порядка, то r (A) = 2.
 2015-02-27
2015-02-27 2959
2959