Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений. Пусть корень 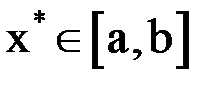 , т. е.
, т. е. 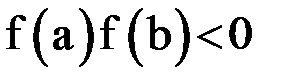 . Предполагаем, что функция
. Предполагаем, что функция 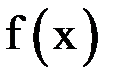 непрерывна на отрезке
непрерывна на отрезке 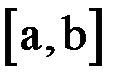 и дважды непрерывно дифференцируема на интервале
и дважды непрерывно дифференцируема на интервале 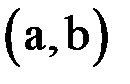 . Положим
. Положим 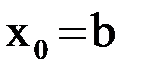 . Проведем касательную к графику функции
. Проведем касательную к графику функции 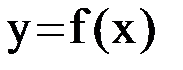 в точке
в точке 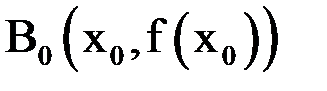 (рис. 1.8).
(рис. 1.8).
Уравнение касательной будет иметь вид: 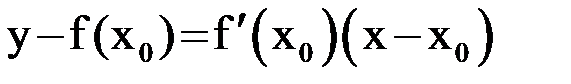 .
.
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью 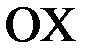 , т. е. положив
, т. е. положив 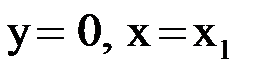 :
: 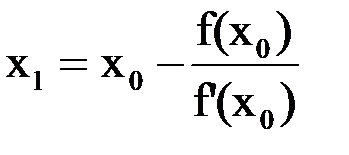 .
.
Аналогично поступим с точкой 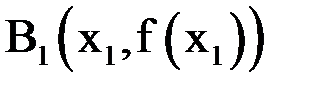 , затем с точкой
, затем с точкой 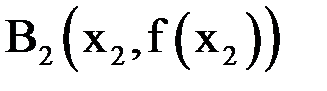 и т. д., в результате получим последовательность приближений
и т. д., в результате получим последовательность приближений 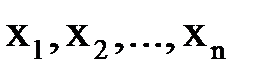 , причем
, причем
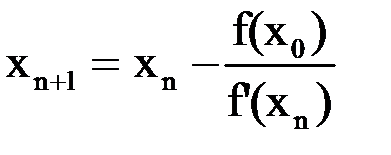 . (1.6)
. (1.6)
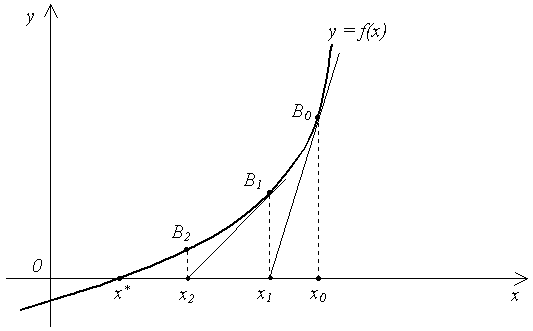
Рисунок 1.8 - Касательная к графику функции 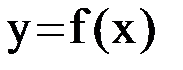 в точке
в точке 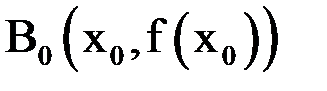
Формула (1.6) является расчетной формулой метода Ньютона.
Метод Ньютона можно рассматривать как частный случай метода простых итераций, для которого 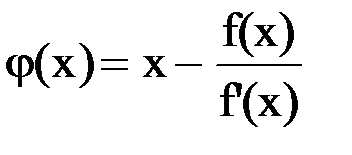 .
.
Сходимость метода. Сходимость метода Ньютона устанавливает следующая теорема.
Теорема. Пусть 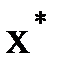 – простой корень уравнения
– простой корень уравнения 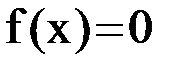 и в некоторой окрестности этого корня функция
и в некоторой окрестности этого корня функция 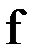 дважды непрерывно дифференцируема. Тогда найдется такая малая
дважды непрерывно дифференцируема. Тогда найдется такая малая  – окрестность корня
– окрестность корня 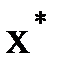 , что при произвольном выборе начального приближения
, что при произвольном выборе начального приближения 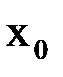 из этой окрестности итерационная последовательность, определенная по формуле (1.6) не выходит за пределы этой окрестности и справедлива оценка:
из этой окрестности итерационная последовательность, определенная по формуле (1.6) не выходит за пределы этой окрестности и справедлива оценка:
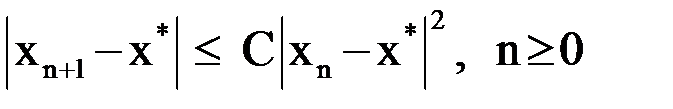 , (1.7)
, (1.7)
где 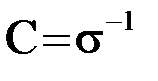 .
.
Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение.
Выбор начального приближения. Пусть 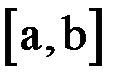 – отрезок, содержащий корень. Если в качестве начального приближения
– отрезок, содержащий корень. Если в качестве начального приближения 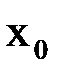 выбрать тот из концов отрезка, для которого
выбрать тот из концов отрезка, для которого 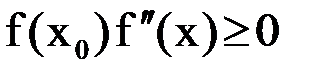 , то итерации (1.6) сходятся, причем монотонно. Рисунок 8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка:
, то итерации (1.6) сходятся, причем монотонно. Рисунок 8 соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка: 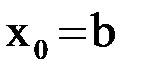 (Здесь
(Здесь 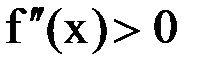 ).
).
Погрешность метода. Оценка (1.7) неудобна для практического использования. На практике пользуются следующие оценки погрешности:
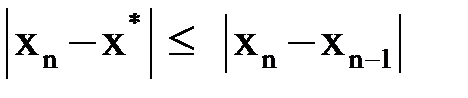 . (1.8)
. (1.8)
Критерий окончания. Оценка (1.8) позволяет сформулировать следующий критерий окончания итераций метода Ньютона. При заданной точности 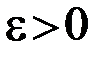 вычисления нужно вести до тех пор, пока не будет выполнено неравенство
вычисления нужно вести до тех пор, пока не будет выполнено неравенство
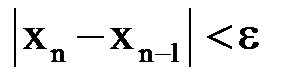 .
.
Пример 1.3. Вычислить методом Ньютона отрицательный корень уравнения 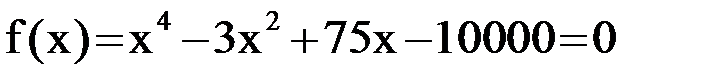 с точностью до 0,0001. Проведя отделение корня, можно убедиться, что корень локализован на интервале
с точностью до 0,0001. Проведя отделение корня, можно убедиться, что корень локализован на интервале 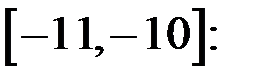
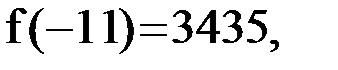
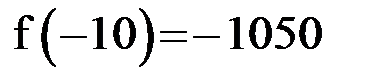 . В этом интервале
. В этом интервале 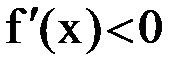 и
и 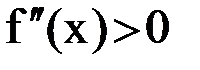 . Так как
. Так как 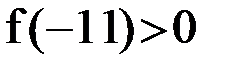 и
и 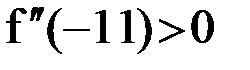 , то за начальное приближение можно принять
, то за начальное приближение можно принять 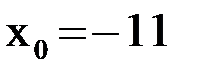 .
.
Таблица 1.3 – Расчётные значения
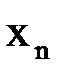
| 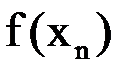
| 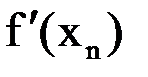
| 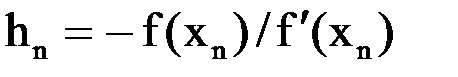
|
| -11 | -5183 | 0,6662 | |
| -10,3336 | 307,3 | 4276,8 | 0,0718 |
| -10,2618 | 3,496 | 4185,9 | 0,0008 |
| -10,261 | 0,1477 | - | - |
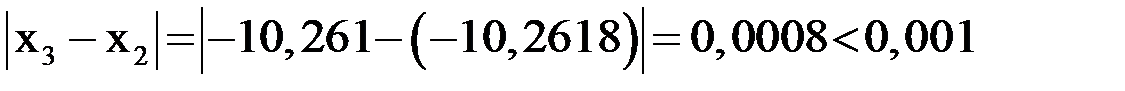 . Поэтому
. Поэтому 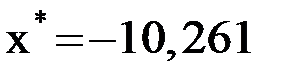 .
.
 2015-02-27
2015-02-27 3714
3714
