Оптимального решения

Если в только что рассмотренной задаче первое же полученное базисное решение оказалось допустимым, то в других случаях его можно найти не сразу, а через некоторое число шагов.

При этом надо помнить, что на первом этапе симплексного метода, т. е. при нахождении какого-либо допустимого решения, линейная форма в расчет не берется, а все преобразования относятся только к системе ограничений.

Пусть задача линейного программирования задана в общем виде, т.е. системой m линейных уравнений с n переменными (m <n) (или же она приведена к такому виду после введения добавочных неотрицательных переменных). Выберем группу m основных переменных, которые позволяют найти исходное базисное решение (не нарушая общности, можем считать, что основными яв­ляются первые m переменных). Выразив эти основные переменные через неос­новные, получим систему ограничений в виде

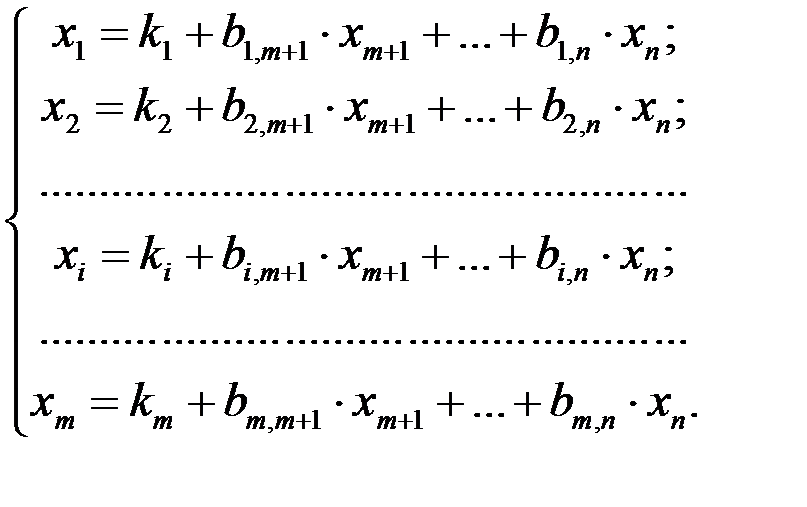
Следовательно, этому способу разбиения переменных на основные и неосновные соответствует базисное решение 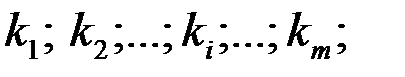…; 0; 0;…;0.

Рассмотрим общий случай, когда это решение является недопустимым. От полученного базисного решения следует сначала перейти к какому-нибудь допустимому базисному решению, причем не обязательно, чтобы этот переход осуществлялся сразу, в один шаг.

Если система ограничений не противоречива, то через конечное число шагов будет осуществлен переход к допустимому базисному решению.

По предположению, исходное базисное решение является недопустимым. Следовательно, среди свободных членов системы ограничений имеется хотя бы один отрицательный (число отрицательных свободных членов этой системы совпадает с числом отрицательных компонент исходного базисного решения). Пусть им является свободный член k_i i-ro уравнения, т. е. основная переменная x_i в соответствующем базисном решении отрицательна.

Для перехода к новому базисному решению необходимо решить два вопроса:

1) установить, какая неосновная переменная должна быть переведена в число основных;

2) выбрать переменную, которую из основных следует пере­вести в неосновные на место выбывшей в основные переменной.

При переводе неосновной переменной в основные она не убывает, а, как правило, возрастает: вместо нуля в исходном базисном решении она примет положительное значение в новом базисном решении (исключение имеет место только при вырождении). Поэтому для решения вопроса о том, какие неосновные переменные можно перевести в основные, нужно уметь находить неосновные переменные, при увеличении которых возрастает основная переменная, от­рицательная в исходном базисном решении. Вернемся к i-му уравнению системы, в котором свободный член k_i отрицателен. Оно показывает, что переменная x_i возрастает при возрастании тех неосновных переменных, коэффициенты которых в этом уравнении положительны. Отсюда следует, что в основные можно переводить те неосновные переменные, которые в уравнении системы с отрицательным свободным членом имеют положительные коэффициенты.

Здесь могут представиться три случая.

1. В i-м уравнении системы нет неосновных переменных с положительными коэффициентами, т. е. все коэффициенты b_i,j отрицательны (как и свободный член k_i). В этом случае данная система ограничений несовместна – она не имеет ни одного допустимого решения. Действительно, вследствие неотрицательности всех переменных, в том числе x_m+l,...,x_n, i -го уравнения, в котором свободный член k_i и все коэффициенты b_i,m+l,...,b_i,n отрицательны, следует, что переменная x_i - не может принимать неотрицательных значений. Но если нет ни одного допустимого решения системы ограничений, то нет и оптимального.

2. В i-м уравнении имеется одна переменная х_т+j,коэффициентпри которой положителен. В этом случае именно эта переменная переводится в основные.

3. В i-м уравнении имеется несколько переменных с положительными коэффициентами. В этом случае в основные можно перевести любую из них.

Далее необходимо установить, какая основная переменная должна быть переведена в число неосновных. Для этого следует воспользоваться правилом: находят отношения свободных членов к коэффициентам при переменной, переводимой в основные, из всех уравнений, где знаки свободных членов и указанных коэффициентов противоположны, а затем рассматривают абсолютную величину этих отношений и из них выбирают наименьшую (если в некоторых уравнениях знаки свободных членов и коэффициентов совпадают или в каких-то уравнениях переменная, переводимая в основные, отсутствует, то отношение считают равным ∞).

Уравнение, из которого получено наименьшее отношение, выделяют. Выделенное уравнение показывает, какая из основных переменных должна быть переведена в неосновные. Выразив новые основные переменные через неосновные, переходят к следующему базисному решению.

В результате получается аналогичная системе система уравнений, в которой число отрицательных свободных кленов либо совпадает с их числом в системе, либо на единицу меньше. Это зависит от того, положителен или отрицателен свободный член в выделенном уравнении.

Если в выделенном уравнении свободный член отрицателен, то в новом базисном решении число отрицательных компонент окажется на единицу меньше, чем в исходном. Если же в выделенном уравнении свободный член положителен (или равен нулю), то в новом базисном решении число отрицательных компонент останется таким же, как и в исходном.

Итак, получается новое, улучшенное базисное решение, которое ближе к области допустимых решений системы ограничений. Если оно окажется недопустимым, то к нему следует применить ту же схему еще раз. В результате через конечное число шагов получится допустимое базисное решение.

Продолжения примера 4.1. Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму .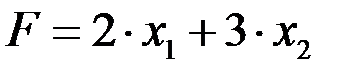

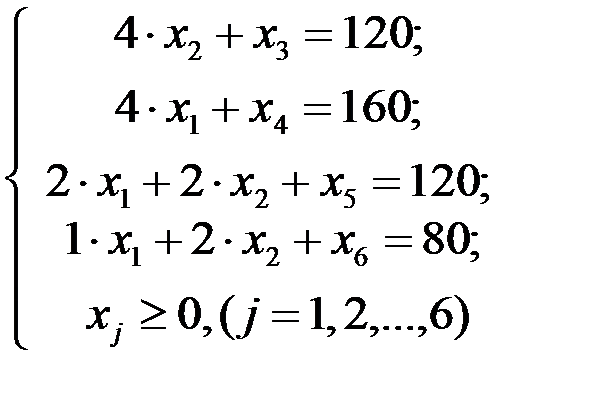
Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число основных переменных должно равняться четырем, а число неосновных - двум.

Для решения задачи симплексным методом, прежде всего, нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаочно взять в качестве основных добавочные переменные х ₃, х ₄, х ₅, х ₆. Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая неосновные переменные х ₁, x ₂ равными нулю, получим базисное решение (0; 0; 120; 160; 120; 80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода.

Переходим сразу ко второму этапу, т. е. к поискам оптимального решения.

1 шаг. Основные переменные: х₃, х₄, х₅, х₆; неосновные переменные: х ₁, x ₂. В системе основные переменные выразим через неосновные. Для того чтобы судить, оставить ли неосновные переменные в числе неосновных или их выгоднее с точки зрения приближения к оптимальному решению перевести в основные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные х ₁, x ₂)• Тогда получим:

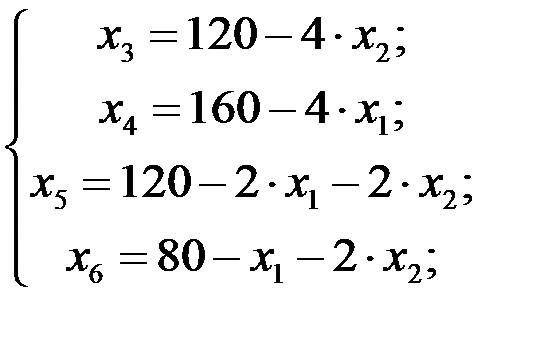
При х ₁ = х ₂ = 0 имеем х ₃ = 120, х ₄ = 160, х ₅ = 120, х ₆ = 80, что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы 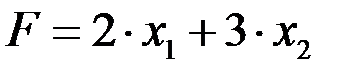=0.

Когда мы полагали х ₁ = х ₂ = 0 (производство ничего не выпускает), была поставлена цель - найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных х ₁ и х ₂. Иными словами, эти переменные невыгодно считать неосновными, т. е. равными нулю, их нужно перевести в число основных. Это и оз­начает переход к новому базисному решению. При симплексном методе на каждом шаге решения предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных переменную х ₂, так как она входит в выражение линейной формы с большим коэффициентом.

Как только одна из свободных переменных переходит в число основных, одна из основных должна быть переведена на ее место в число неосновных. Какую же из четырех основных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения.

Значение х ₂ необходимо сделать как можно большим, так как это соответствует конечной пели - максимизации F. Однако оказывается, что увеличение х ₂ может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование неотрицательности переменных. Так, из первого уравнения системы следует, что переменная х₂ не должна превышать числа 120/4, т. е. х ₂≤30, поскольку только при этих значениях х ₂ переменная х ₃ остается положительной (если х ₂ = 30, то х ₃ = 0; если же х ₂ >30, то х ₃ < 0). Из третьего уравнения системы следует, что х ₂ ≤ 120/2, т. е. х ₂ ≤ 60, из четвертого - что х ₂ ≤ 80/2, т. е. х ₂ ≤ 40 (во второе уравнение переменная х ₂ не входит). Всем этим условиям удовлетворяет х ₂ ≤ 30.

Иными словами, для ответа на вопрос, какую переменную нужно пере­вести в число неосновных, нужно принять х ₂ = min {120/4; 120/2; 80/2} = min {30; 60; 40} = 30. Тогда х ₃ = 0 и х ₃ переходит в число неосновных переменных, а х₄ и х₅ останутся положительными,

2 шаг. Основные переменные: х ₂, х ₄, х ₅, х ₆ неосновные переменные: х ₁и х ₃. Выразим основные переменные и линейную форму через неосновные. В системе берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при х ₂. В данном случае это первое уравнение. Выразив из этого уравнения х ₂, имеем, х ₂ = 30 - 0.25 · х ₃. Подставим это выражение х ₂ во все остальные уравнения системы (4.4) и в линейную форму F и, приведя подобные члены, получим

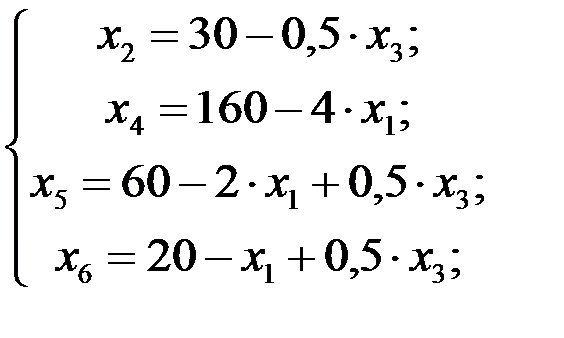(4.5)

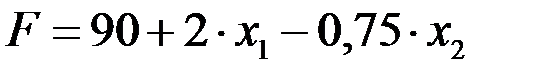
При х ₁ = х ₃ = 0 имеем F = 90. Это уже лучше, чем на 1 шаге, но не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной х ₁ в число основных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать неосновной, т.е. равной нулю.

Для ответа на вопрос, какую переменную вывести из основных в неосновные, примем х ₁ = min {160/4; 60/2; 20/1} = 20. Тогда х ₆ = 0 и х ₆ переходит в число неосновных переменных, а х ₄ и х ₅, остаются при этом положительными.

Первое уравнение не используется при нахождении указанного минимума, так как х _] не входит в это уравнение.

3 шаг. Основные переменные: х ₁ ,х₂, х₄, х₅; неосновные переменные: х₃, х₆. Выразим основные переменные и линейную форму через неосновные. Из последнего уравнения системы (4.5) (оно выделено) имеем х ₁ = 20 + 0.5 · х ₃ - х ₆. Подставляя это выражение в остальные уравнения и в линейную форму, получим

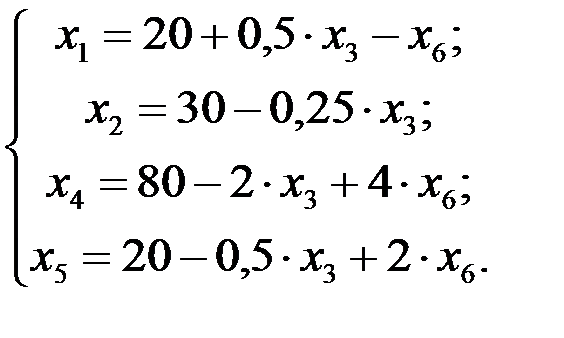(4.6)

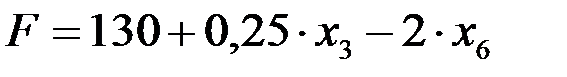
Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение F за счет введения в основные переменной х ₃ (она имеет положительный коэффициент). Полагаем х ₃ = min {∞; 30/0,25; 80/2; 20/0,5} =40.

Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений.

Во-первых, хотя переменная х ₃ и входит в выражение для х ₁(первое уравнение системы (4.6), но имеет положительный коэффициент и при любом возрастании х ₃ переменная х ₁не может стать отрицательной. Иными словами, в первом уравнении никаких ограничений на возрастание переменной х ₃ не накладывается, поэтому мы условно пишем ∞. Условимся в дальнейшем пользоваться этим же обозначением, если переменная, вновь вводимая в число основных, не входит в какое-либо уравнение системы ограничении.

Во-вторых, мы получим два одинаковых минимальных значения, равные 40. Если х ₃ = 40, то х ₄ = 0 и х₅ = 0, т. е. напрашивается вывод, что вместо одной переменной нужно перевести в число неосновных сразу две: х ₄ и х₅. Но число основных переменных не должно быть меньше четырех. Для этого поступают следующим образом. Одну из переменных (х ₄ или х ₅.) оставляют в числе основных, но при этом ее значение считают равным нулю, т. е. полученное на следующем шаге базисное решение оказывается вырожденным. Оставим, например, х ₄ в числе основных переменных, а х ₅ переведем в число неосновных.

4 шаг. Основные переменные: х ₁, х₂, х ₃, х ₄; неосновные переменные: х₅, х₆. Выразим основные переменные и линейную форму F через неосновные, начав это выражение из четвертого уравнения системы (4.6). В итоге получим

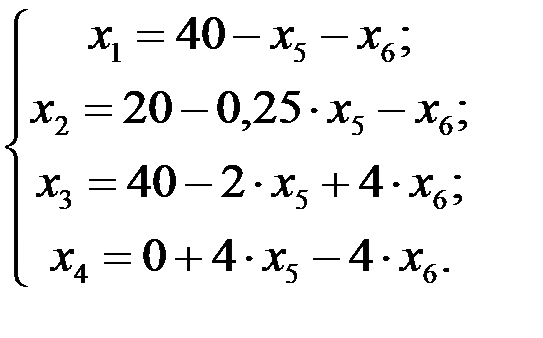
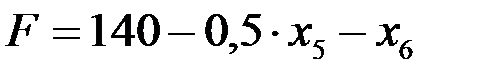
Так как в выражение линейной формы переменные х ₅ и х ₆ входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно.

Отсутствие на каком-то шаге симплексного метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с положительными коэффициентами является критерием оптимальности.

Следовательно, на 4 шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (40; 20; 40; 0; 0; 0), при котором F _max=140. Таким образом, для получения наибольшей прибыли, равной 140 ден. ед., из данных ресурсов необходимо получить 40 единиц продукции с сенокосов и 20 с пашни. При этом ресурсы II, III и IV видов окажется использованной полностью, а 40 ед. I вида останутся неизрасходованными.

Пример 4.2. Найти максимум функции F = х ₁+ 2· х ₂ при ограничениях

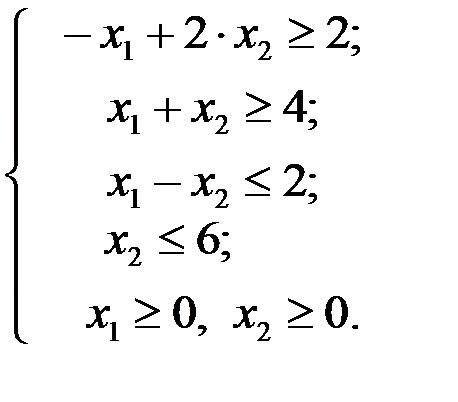
Вводим добавочные неотрицательные переменные х ₃, х ₄, х ₅, х ₆ и сводим данную систему неравенств к эквивалентной ей системе уравнений

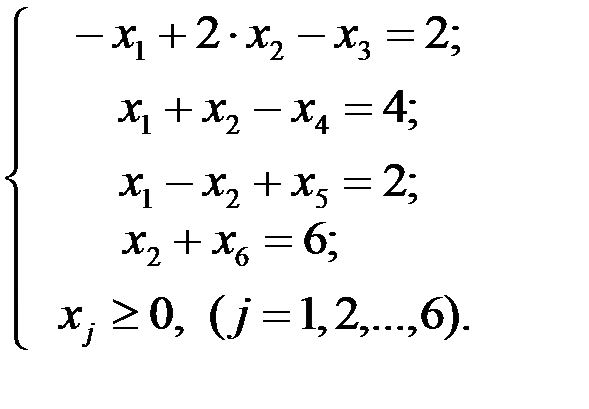
Введенные добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда х ₁и х ₂ - неосновные переменные.

1 шаг. Основные переменные: х ₃, х ₄, х ₅, х ₆; неосновные перемен­ные; х ₁ и х ₂. Выразив основные переменные через неосновные, получим

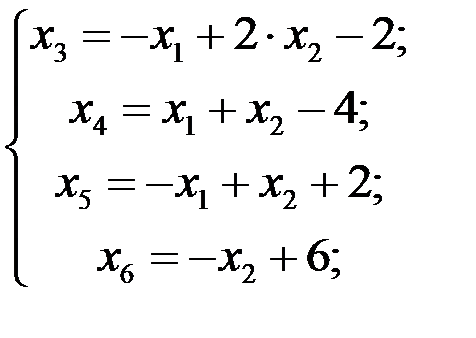
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение (0; 0; - 2; - 4; 2; 6), которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдем к улучшенному.

Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести х ₁ и х ₂, так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, что произойдет, если переведем любую из них в основные переменные, переменная х ₄ увеличится).

Попробуем перевести в основные переменную х ₁. Чтобы установить, какую переменную следует перевести из основных в неосновные, найдем абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при х ₁, имеем х ₁= min (∞; 4/1; 2/1; ∞) = 2. Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную х ₅, которая в исходном базисном решении положительна.

Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдет.

Если же перевести в основные переменную х ₂, то наименьшее отношение свободных членов к коэффициентам при х ₂ составит х ₂ - min (2/2; 4/1; ∞; 6/1) = 1. Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя х ₂в основные, а х ₃ в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим х ₂в основные, а х ₃ в неосновные переменные; тогда выделенным окажется первое уравнение.

2 шаг. Основные переменные: х ₂, х ₄, х ₅, х ₆; неосновные переменные: х ₁ и х ₃. Выразим новые основные переменные через новые неосновные, начиная это делать с выделенного на 1 шаге уравнения. В результате получим

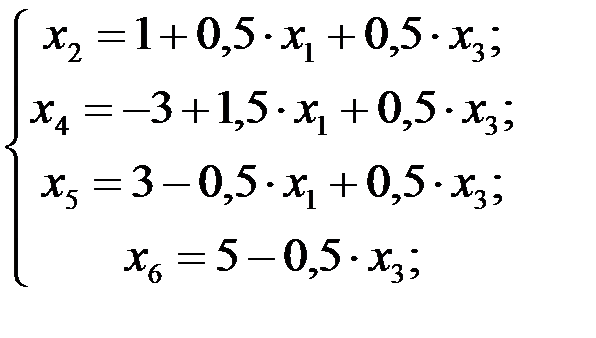
Следовательно, имеем новое базисное решение (0; 1; 0; -3; 3; 5), которое также является недопустимым, а поэтому не оптимальным. Но в нем, как мы и предвидели, только одна переменная отрицательна (а именно х ₄).

От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т.е. второе уравнение. Оно показывает, что в основные переменные можно перевести х ₁ и х ₃. Переведем в основные переменные х ₁. Найдем наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при х ₁; имеем х ₁ = min (∞; 3/1,5; 3/0,5; 5/0,5) = 2. Значит, в неосновные переменные нужно перевести х ₄. Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.

3 шаг. Основные переменные: х ₁, х ₂, х ₅, х ₆; неосновные переменные: х ₃, х ₄. Выразив основные переменные через неосновные, получим

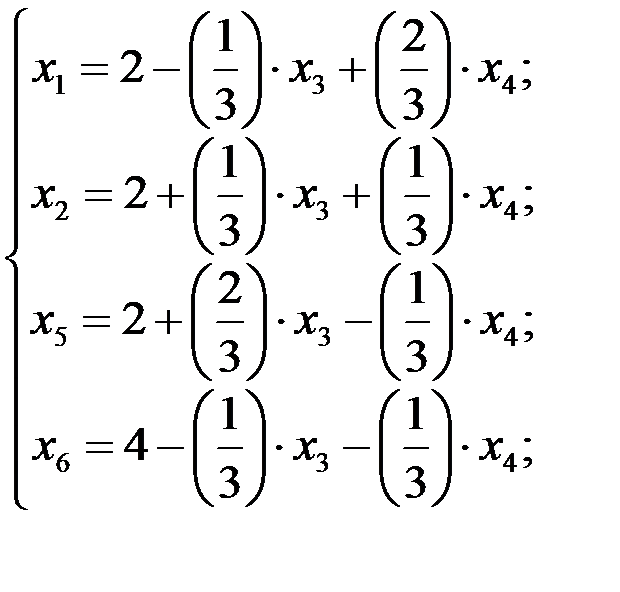
Новое базисное решение имеет вид (2; 2; 0; 0; 2; 4). Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Таким образом, к линейной форме обращаемся только тогда, когда базисное решение является допустимым. Так как мы ищем максимум линейной формы, то полученное базисное решение не оптимальное.

Переводим в число основных переменную х ₄ имеющую больший положительный коэффициент.

Находим х ₄ = min (∞; ∞; 2: (1/3); 4/(1/3)) = 6. Это наименьшее отношение получено из третьего уравнения системы, которое и выделяем. Оно показывает, что при х ₄ =6 переменная х ₅ = 0 и поэтому перейдет в число неосновных.

4 шаг. Основные переменные: х ₁, х ₂, х ₄, х ₆;неосновные переменные: х ₃, х ₅. Выразив основные переменные через неосновные, получим

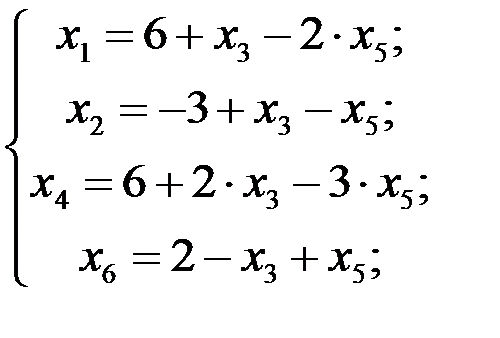
Линейная форма, выраженная через те же неосновные переменные, примет вид 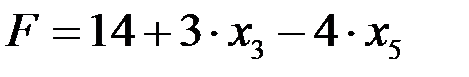. Следовательно, базисное решение (6; 4; 0; 6; 0; 2), к которому мы перешли, не является оптимальным.

Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная х₃ является основной. Находим х ₃ = min {∞; ∞; со; 2/1} = 2. Это наименьшее отношение получено из четвертого уравнения системы и показывает, чго при х ₃ = 2 переменная х ₆ = 0 и переходит в число неосновных.

5 ш а г. Основные переменные: х ₁, х ₂, х ₃, х ₄ неосновные переменные х ₅, х ₆.Выразив основные переменные через неосновные, получим

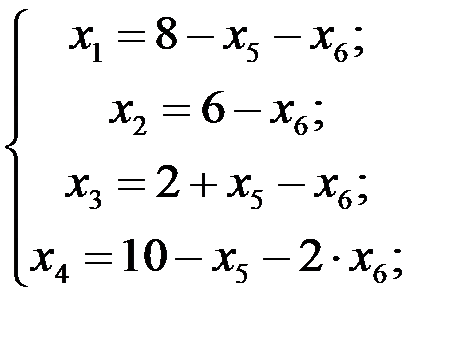
Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид 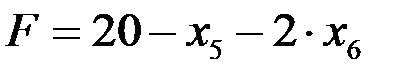. Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение (8; 6; 2; 10, 0; 0) является оптимальным, а максимум линейной формы F _max = 20.

4.5 Графическое решение задач

линейного программирования

Графический способ решения задач линейного программирования целесообразно использовать для:

• решения задач с двумя переменными, когда ограничения выражены неравенствами;

• решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

Запишем задачу линейного программирования с двумя переменными:

целевая функция:

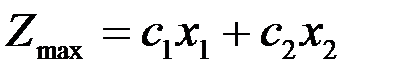(4.7)

ограничения:

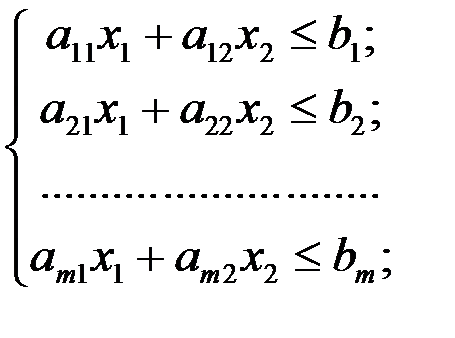(4.8)

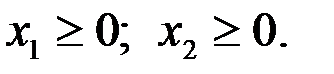
Каждое из неравенств (4.8) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми 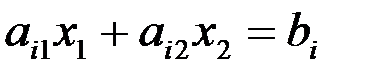; 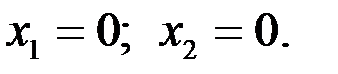. В том случае, если система неравенств (4.8) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей - выпуклое, то областью допустимых ре­шений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств.

Областью допустимых решений системы неравенств (4.8) может быть:

• выпуклый многоугольник;

• выпуклая многоугольная неограниченная область;

• пустая область;

• луч;

• отрезок;

• единственная точка.

Целевая функция (4.7) определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение Z.

Вектор 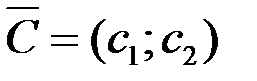c координатам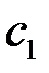и и 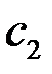, перпендикулярный этим прямым, указывает направление наискорейшего возрастания Z, а противоположный вектор - направление убывания Z.

Если в одной и той же системе координат изобразить область допустимых решений системы неравенств (4.8) и семейство параллельных прямых (4.7), то задача определения максимума функции Z сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства Z = const, и которая соответствует наибольшему значению параметра Z.

Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

Для определения данной вершины построим линию уровня 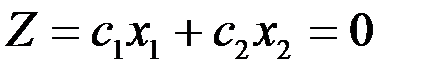проходящую через начало координат и перпендикулярную вектору 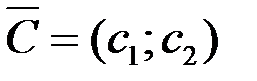, и будем передвигать ее в направлении вектора 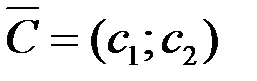до тех пор, пока она не коснется последней крайней (угловой) точки многоугольника решений. Координаты указанной точки и определяют оптимальный план данной задачи.

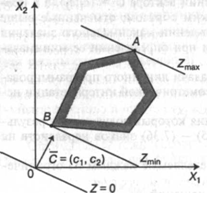
Рисунок 4.1 - Оптимум функции Z достижим в точке А

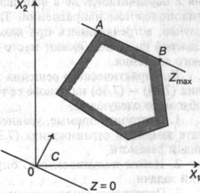
Рисунок 4.2 - Оптимум функции Z достигается в любой точке [АВ]

Заканчивая рассмотрение геометрической интерпретации задачи (4.7) - (4.8), отметим, что при нахождении ее решения могут встретиться случаи, изображенные на рис. 4.1 - 4.4. Рисунок 4.1 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рисунка 4.2 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ.

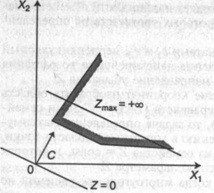
Рисунок 4.3 - Оптимум функции Z недостижим

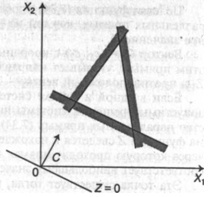
Рисунок 4.4 - Область допустимых решений - пустая область

На рисунке 4.3 изображен случай, когда максимум недостижим, а на рисунке 4.4 — случай, когда система ограничений задачи несовместна. Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня Z передвигается не в направлении вектора 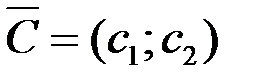, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Для практического решения задачи линейного программирования (4.7) - (4.8) на основе ее геометрической интерпретации необходимо следующее.

1.Построить прямые, уравнения которых получаются в результате замены в ограничениях (4,4) знаков неравенств на знаки равенств.

2.Найти полуплоскости, определяемые каждым из ограничений задачи.

3.Определить многоугольник решений.

4.Построить вектор .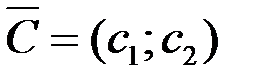

5.Построить прямую 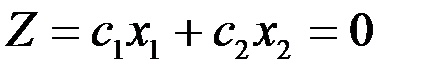, проходящую через начало координат и перпендикулярную вектору .

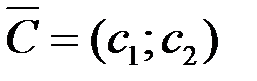6.Передвигать прямую 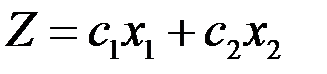в направлении вектора 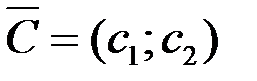, в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.

7.Определить координаты точки максимума функции и вычислить значение целевой функции в этой точке.

Пример 4.3. Предприятие изготавливает два вида продукции П и Р, которая поступает в оптовую продажу. Для производства продукции используют два вида сырья А и Б. Максимально возможные запасы сырья в сутки составят 9 и 13 единиц соответственно. Расход сырья вида А на производство продукции П и Р составят 2 и 3 единицы соответственно, вида Б 3 и 2 единицы. Опыт работы показал, что суточный спрос на продукцию П никогда не превышает спроса на продукцию Р более чем на 1 единицу. Кроме того известно, что спрос на продукцию Р никогда не превышает 2 единицы в сутки. Оптовые цены единицы продукции равны 3 единицы для П, и 4 единицы для Р. Какое количество продукции каждого вида должно произвести предприятие, чтобы доход от реализации был максимальным. Решить задачу геометрическим способом.

Решение. Построим многоугольник решений (рис. 7.5). Для этого в системе координат X₁OX₂ на плоскости изобразим граничные прямые:

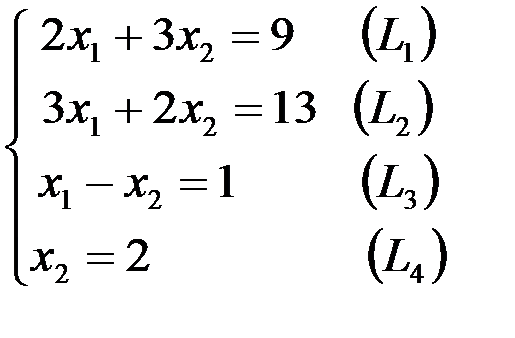
Взяв какую-либо точку, например начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рис. 7.5 показаны стрелками. Областью решений является многоугольник OABCD.

Для построения прямой 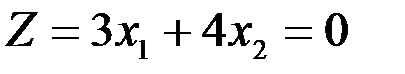строим вектор-градиент 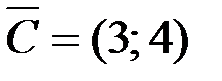и через точку 0 проводим прямую, перпендикулярную ему. Построенную прямую Z= 0 перемещаем параллельно самой себе в направлении вектора 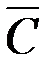. Из рисунок 4.5 следует, что по отношению к многоугольнику решений опорной эта прямая становится в точке С, где функция принимает максимальное значение. Точка С лежит на пересечении прямых L₁ и Z₃. Для определения ее координат решим систему уравнений:

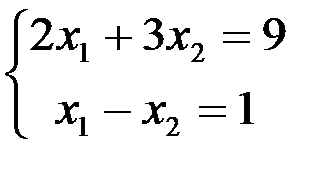
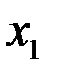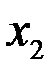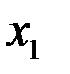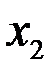Оптимальный план задачи = 2,4; =1,4. Подставляя значения и в линейную функцию, получим:

= 3 • 2,4 + 4 • 1,4 = 12,8.

Полученное решение означает, что объем производства продукции П должен быть равен 2,4 ед., а продукции Р - 1,4 ед. Доход, получаемый в этом случае, составит: Z = 12,8 д. е.

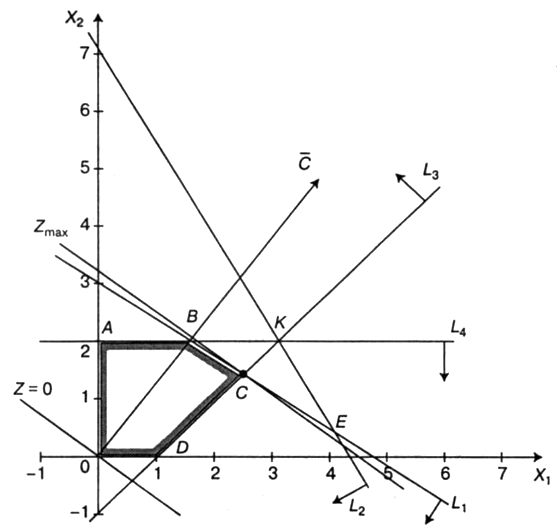
Рисунок 4.5 - Решение задачи линейного программирования геометрическим способом

5. ДВОЙСТВЕННЫЕ ЗАДАЧИ

Составление двойственной задачи. Рассмотрим две задачи линейного программирования:

Максимизировать функцию

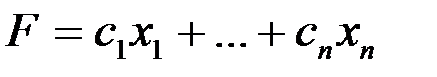
при ограничениях

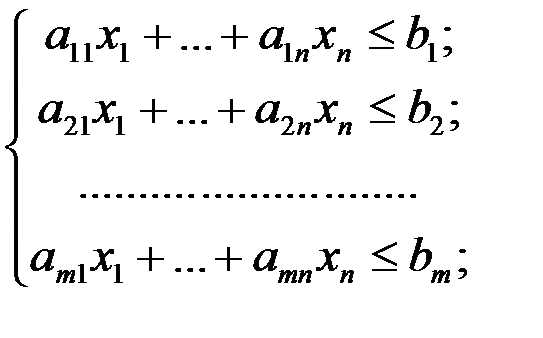
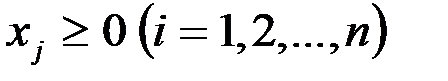
Минимизировать функцию

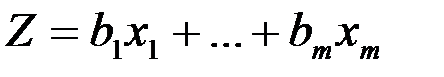
при ограничениях

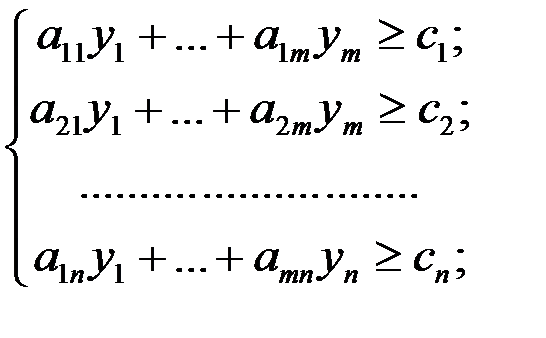
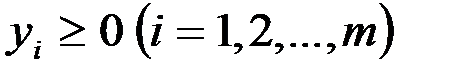
Эти задачи обладают следующими свойствами:

1. В одной задаче ищется максимум линейной формы, а в другой – минимум.

2°. Коэффициенты при переменных в линейной форме одной задачи являются свободными членами системы ограничений другой задачи, наоборот, свободные члены системы ограничений одной задачи – коэффициентами при переменных в линейной форме другой задачи.

3°. В каждой задаче система ограничений задается в виде неравенств, причем все они одного смысла, а именно: при нахождении максимума линейной формы эти неравенства имеют вид, а при нахожде­нии минимума – вид

4°. Коэффициенты при переменных в системах ограничений описываются матрицами

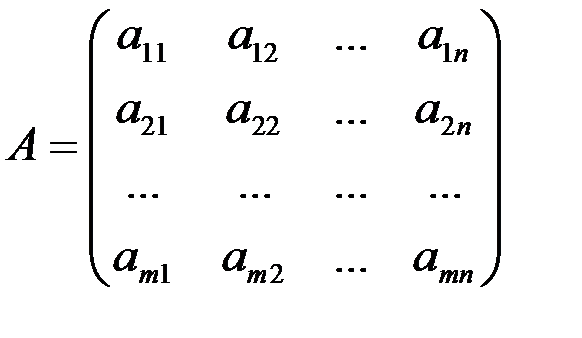и

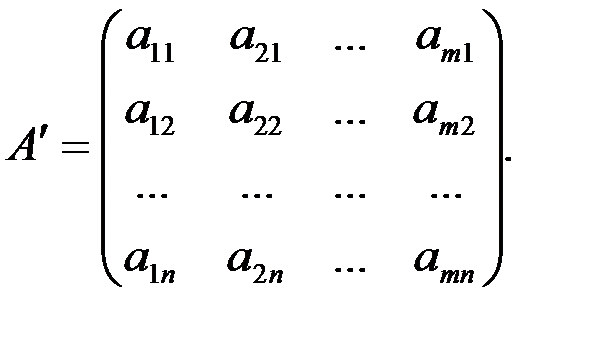
которые являются транспонированными относительно друг друга.

5°. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6^е. Условия неотрицательности переменных сохраняются в обеих задачах.

Две задачи линейного программирования, удовлетворяющие указанным выше условиям, называются симметричными взаимно двойственными задачами. Мы будем изучать только симметричные двойственные задачи, а поэтому будем называть их короче – двойственными задачами.

Таким образом, каждой задаче линейного программирования можно поставить в соответствие двойственную ей задачу. Первоначальную задачу будем называть исходной (или прямой). Прямая и двойственная ей задача, взятые вместе, образуют пару взаимно двойственных задач, причем любую из них можно рассматривать как исходную, тогда другая окажется двойственной ей.

Из сказанного вытекают следующие правила составления задачи, двойственной по отношению к исходной:

1. Приводят все неравенства системы ограничений исходной задачи к неравенствам одного смысла: если в исходной задаче ищется максимум линейной формы – к виду ≤, если же минимум – к виду ≥. Для этого неравенства, в которых это требование не выполняется, умножают на - 1.

2. Выписывают матрицу А коэффициентов при переменных исходной задачи, полученных после преобразования п. 1, и составляют матрицу А', транспонированную относительно матрицы А.

3. Составляют систему ограничений двойственной задачи, взяв в качестве коэффициентов при переменных элементы матрицы А', а в качестве свободных членов – коэффициенты при переменных в линейной форме исходной задачи, и записывают неравенства противоположного смысла по сравнению с неравенствами, полученными в п. 1.

4. Составляют линейную форму двойственной задачи, приняв за коэффициенты при переменных свободные члены системы ограничений исходной задачи, полученные в п. 1.

5. Указывают, что необходимо найти при решении двойственной задачи, а именно: минимум линейной формы, если в исходной задаче ищется максимум, и максимум, если в исходной задаче ищется минимум.

6. Записывают условие неотрицательности переменных двойственной задачи.

Пример 5.1. Составить задачу, двойственную следующей: найти максимум функции 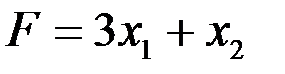при ограничениях

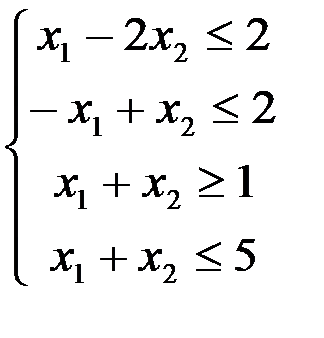
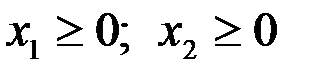
Третье неравенство системы (*) не удовлетворяет п. 1 правил составления двойственной задачи. Поэтому умножим его на –1:

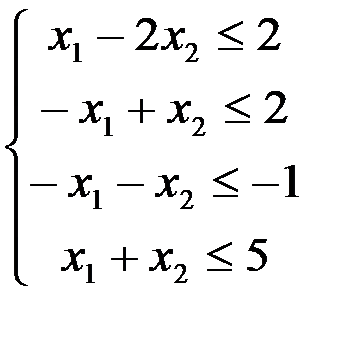
Для облегчения составления двойственной задачи лучше пользоваться рас­ширенной матрицей В, в которую наряду с коэффициентами при переменных системы ограничений исходной задачи запишем свободные члены и коэффициенты при переменных в линейной форме, выделив для этой цели дополнительные столбец и строку. Матрицу В транспонируем и, используя транспонированную матрицу В^/, составляем задачу двойственную данной.

,

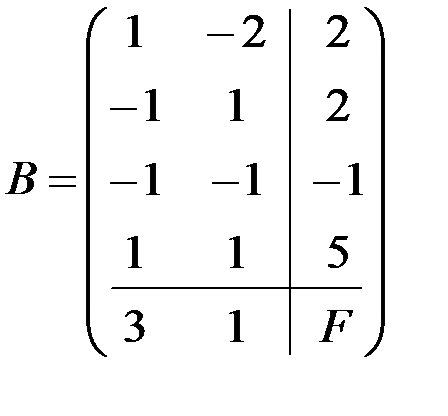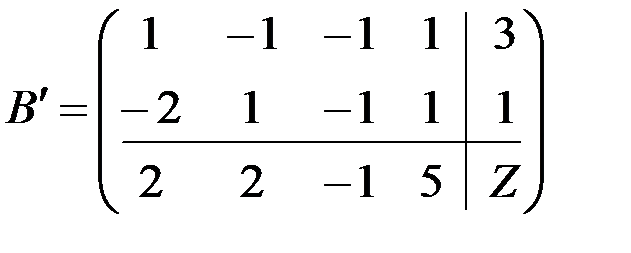
Двойственная задача сводится к нахождению минимума функции 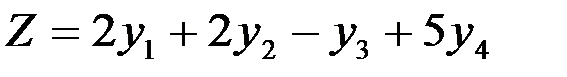при ограничениях

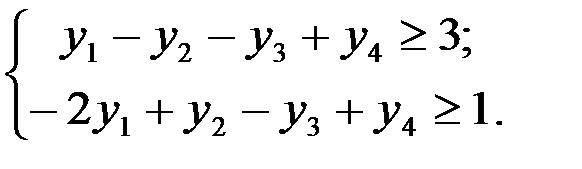
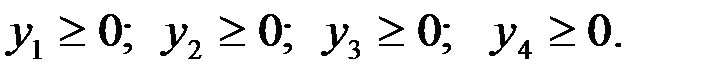
Основные теоремы двойственности

Теория двойственности в линейном программировании строится на следующих основных теоремах.

Теорема 1. Если одна из задач линейного программирования имеет конечный оптимум, то и двойственная к ней также имеет конечный оптимум, причем оптимальные значения линейных форм обеих задач совпадают, т. е. F_max = Z_min или F_min = Z_max. Если же линейная форма одной из двойственных задач не ограничена, то условия другой задачи противоречивы.

Прежде чем сформулировать следующую теорему, установим соответствия между переменными в исходной и двойственной задачах.

При решении симплексным методом исходной задачи для сведения системы неравенств к эквивалентной ей системе уравнений нужно ввести т добавочных неотрицательных переменных (по числу неравенств в системе ограничений) 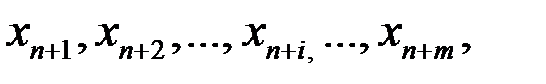где i = 1, 2,…,т означает номер неравенства, в которое была введена добавочная переменная .

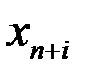Система ограничений двойственной задачи состоит из п неравенств, содержащих т переменных. Если решать эту задачу симплексным ме­тодом, то следует ввести п добавочных неотрицательных переменных 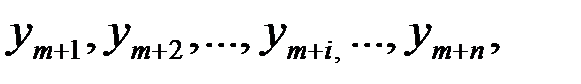где j = 1, 2,…,т означает номер неравенства системы ограничений двойственной задачи, в которое была введена добавочная переменная .

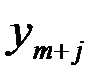Установим следующее соответствие между переменными в исход­ной и двойственной задачах:

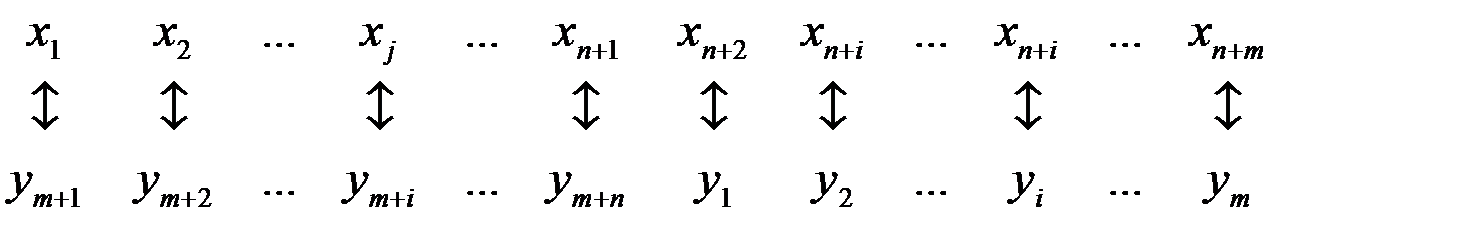
Иными словами, каждой первоначальной переменной исходной
задачи x_j (j = 1,2,…, п) ставится в соответствие добавочная переменная 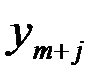, введенная в j - e неравенство двойственной задачи, а каждой добавочной переменной 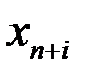исходной задачи (i = 1, 2,…, т), введенной в i - e неравенство исходной задачи, – первоначальная переменная 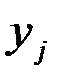двойственной задачи.

Теорема 2.Компоненты оптимального решения одной из задач (прямой или двойственной) равны абсолютным величинам коэффициентов при соответствующих переменных в выражении линейной формы другой задачи (двойственной или прямой) при достижении ею оптимума и при условии, что полученное оптимальное решение не является вырожденным.

Из теорем 1 и 2 следует, что если решить одну из взаимно двойственных задач, т. е. найти ее оптимальное решение и оптимум линейной формы, то можно записать оптимальное решение и оптимум линейной формы другой задачи.

Пример 5.2. Решить симплексным методом прямую и двойственную задачи, приведенные в предыдущем примере.

Решение прямой задачи. Сведем систему ограничений неравенств (см. с. 268) к системе уравнений, введя неотрицательные добавочные переменные:

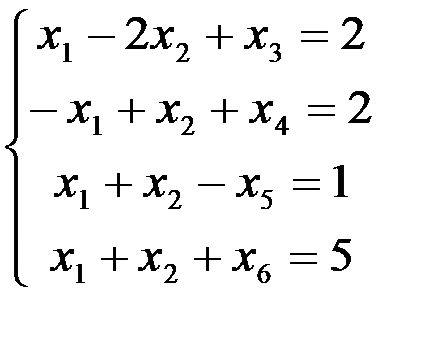
Добавочные переменные х₃, x₄, х₅, x₆ примем за основные на I шаге реше­ния.

1 шаг. Основные переменные: х₃, x₄, х₅, x₆; неосновные переменные: х₁, х₂. Выразим основные переменные через неосновные (линейную форму на этом шаге решения не рассматриваем, так как соответствующее базисное решение не является допустимым):

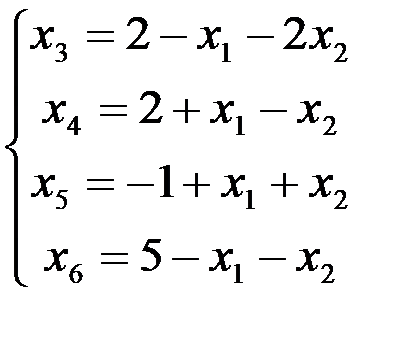
Для получения допустимого базисного решения переменную переведем в основные. Находим = min {2/1; ∞; 1/1; 5/1} = 1. При этом переменная х₅ переходит в неосновные.

2 шаг. Основные переменные: х₁, х₃, х₄, х₆ неосновные переменные; х₂, х₅. Выразим основные переменные и линейную форму через неосновные:

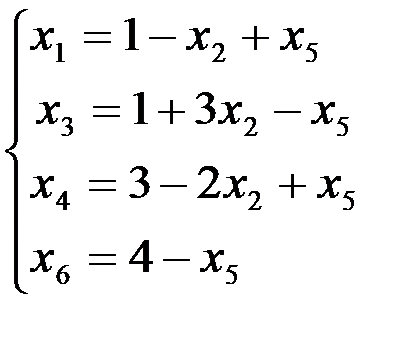
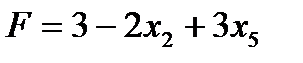
Переведем в основные переменную х₅. Полагая х₅ =min {∞; 1/1; ∞; 4/1} = 1, заключаем, что переменную х₃ нужно перевести в неосновные.

3 шаг. Основные переменные: х₁, х ₄, х₅, х₆, неосновные переменные х₃,х₂. Имеем

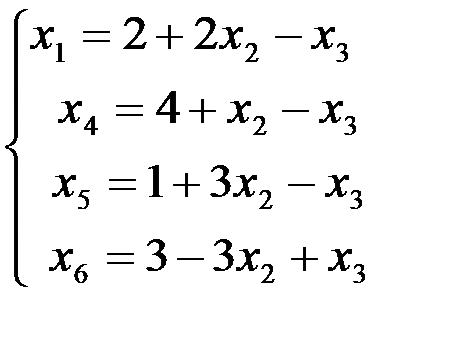
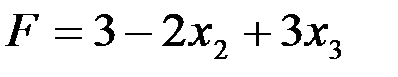
Переменную x₂ переводим в основные. Находим х₂ = min {∞; ∞;∞; 1/1}=1. Тогда переменная х₆ переходит в неосновные.

4 ш а г. Основные переменные:: х₁, х₂, х ₄, х₅,; неосновные переменные: х₂, х₆. Имеем

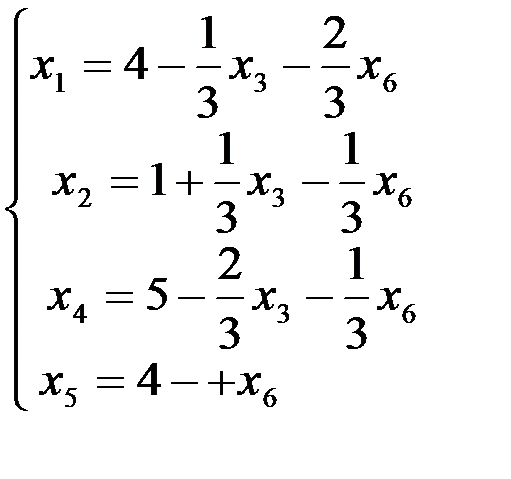
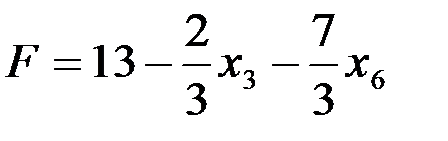
Критерий оптимальности выполнен. Оптимальное решение имеет вид (4; 1; 0; 5; 4; 0); при этом решении F_max = 13.

Продолжение примера 5.1. Систему ограничений двойственной задачи сводим к системе уравнений:

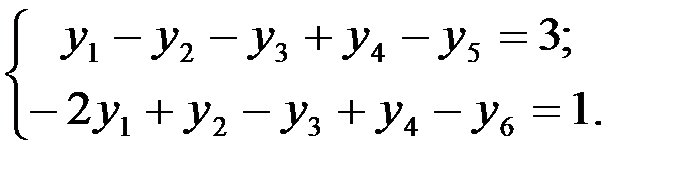
Добавочные переменные y₅ y₆ примем за основные на 1 шаге решения.

1 шаг. Основные переменные: y₅, y₆; неосновные переменные: y₁, у₂, у₃, у₄. Выразим основные переменные через неосновные:

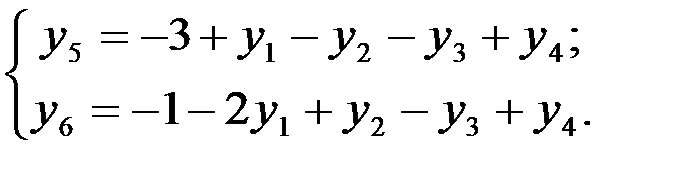
Переведем в основные переменную у₄. Находим у₄ = mm (3/1: 1/1 = 1. Переменная y₆ переходит в неосновные.

2 шаг. Основные переменные: у₄, y₅ неосновные переменные: y₁, у₂, у₃, у₆. Имеем

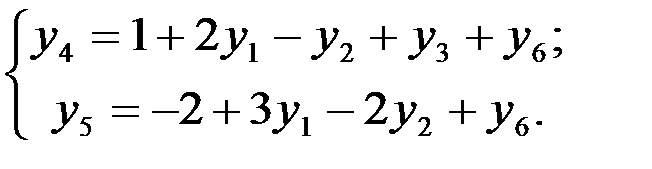
Переменную y₁ переведем в основные. Так как y₁ = min (∞; 2/3) = 2/3, то переменная y₅ переходит в неосновные.

3 шаг. Основные переменные y₁, у₄, неосновные переменные: у₂, у₃, y₅, у₆. Так как соответствующее базисное решение задачи является допустимым, то выразим через неосновные переменные не только основные, но и линейную форму:

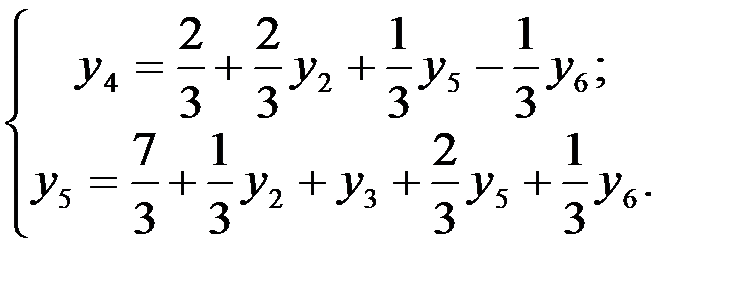
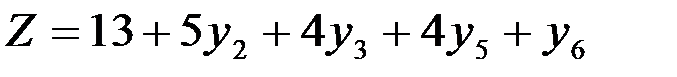
Критерий оптимальности (для случая минимизации линейной формы) вы­полнен. Оптимальное решение имеет вид (2/3; 0; 0; 7/3; 0; 0), при этом Z_min= 13.

Решив двойственную задачу, убеждаемся в справедливости первой части теоремы 1: двойственная задача тоже имеет конечный оптимум, причем Z_min = =F_max = 13.

Убедимся, что справедливо также и утверждение теоремы 2. Для этого запи­шем переменные прямой и двойственной задачи, соблюдая их соответствие;

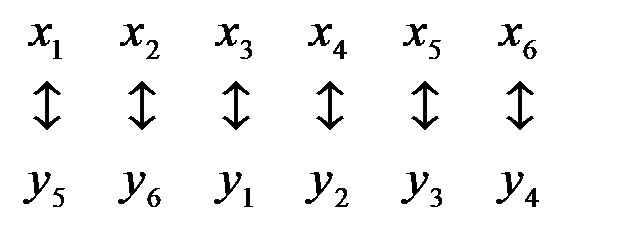
Линейную форму, полученную на последнем шаге решения двойственной задачи, выразим через все переменные этой задачи:

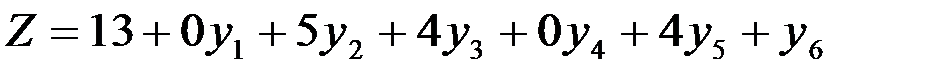
Рассматривая коэффициенты при переменных y_j в этой линейной форме и учитывая их соответствие с коэффициентами при переменных x_i, получим решение (4; 1; 0; 5; 4; 0), совпадающее с оптимальным решением прямой задачи.

Замечание. Решив прямую задачу, можно сразу получить решение двойственной задачи. Если выразить линейную форму F, полученную на 4 шаге решения прямой задачи, через все переменные этой задачи, то получим

.

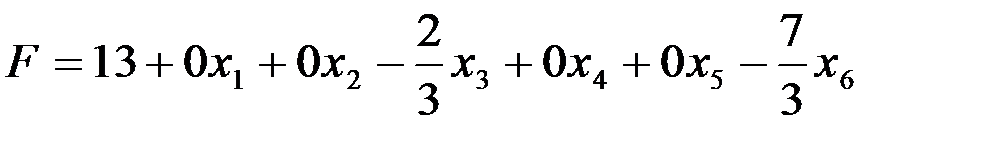На основании теоремы 2, учитывая соответствие между переменными в прямой и двойственной задачах и взяв абсолютную величину коэффициентов при переменных, найдем оптимальное решение двойственной задачи (2/3; 0; 0; 7/3; 0; 0). При этом Z_min =F_max = 13.

6 ТРАНСПОРТНАЯ ЗАДАЧА