Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования.
Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т. е. к системе т линейных уравнений с п переменными (m < n), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм симплексного метода, изложенный выше.
Таким образом, применение симплексного метода распадается на два этапа:
1) нахождение допустимого базисного решения системы ограничений;
2) нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Так как число базисных решений всегда ограничено, то ограничено и число шагов симплексного метода.
Алгоритм симплексного метода:
1. В системе ограничений (уравнений или неравенств) переносят свободные члены в правые части. Если среди этих свободных членов окажутся отрицательные, то соответствующее уравнение или неравенство умножают на - 1.
2. Если система ограничений задана системой неравенств, то вводят добавочные неотрицательные переменные и тем самым сводят систему неравенств к эквивалентной системе уравнений, т. е. сводят задачу к канонической.
3. В данной или полученной после выполнения п. 2 системе m уравнений с п переменными (m < n) m переменных принимают заосновные. Основнымимогут быть любые т переменных, коэффициенты при которых образуют отличный от нуля определитель. Проще всего в качестве основных взять добавочные переменные (в этом случае отпадает необходимость вычислять определитель, который заведомо отличен от нуля, так как каждая добавочная переменная входит только в одно из уравнений системы ограничений).
После этого выражают основные переменные через неосновные и находят соответствующее базисное решение.
Если найденное базисное решение окажется допустимым, то переходят к п. 5; если же оно окажется недопустимым, то предварительно выполняют п. 4.
4. От полученного недопустимого базисного решения переходят к допустимому базисному решению или устанавливают, что система ограничений данной задачи противоречива.
5. Получив допустимое базисное решение, выражают через неосновные переменные этого решения и линейную форму. Если отыскивается максимум (минимум) линейной формы и в ее выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение служит оптимальным, т. е. решение окончено.
6. Если при нахождении максимума (минимума) линейной формы в ее выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, то переходят к новому базисному решению.
Из неосновных переменных, входящих в линейную форму с положительными (отрицательными) коэффициентами, выбирают ту, которой соответствует наибольший (наибольший по абсолютной величине отрицательный) коэффициент, и переводят ее в основные.
7. Чтобы решить, какую из основных переменных следует перевести в неосновные, находят абсолютные величины отношений свободных членов уравнений к коэффициентам при переменной, переводимой в основные, причем только из тех уравнений, в которых эти коэффициенты отрицательны. Для уравнений, в которых указанные коэффициенты положительны или равны нулю (переменная, переводимая в основные, в них отсутствует), эти отношения считают равными со. Из найденных отношений выбирают наименьшее и тем самым решают, какая из основных переменных перейдет в неосновные. Соответствующее уравнение выделяют.
8. Выражают новые основные переменные и линейную форму через неосновные переменные (это начинают делать с выделенного уравнения).
9. Повторяют п. 6…8 до тех пор, пока не будет достигнут критерий оптимальности (см. п. 5). После этого выписывают компоненты оптимального решения и находят оптимум линейной формы.
10.Если допустимое базисное решение дает оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение не единственное.
11.Если в выражении линейной формы имеется неосновная переменная с положительным коэффициентом в случае ее максимизации (с отрицательным в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит с положительными коэффициентами или отсутствует, то линейная форма не ограничена при данной системе ограничений. В этом случае ее максимальное (минимальное) значение записывают в виде
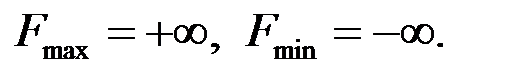
 2015-02-27
2015-02-27 2771
2771








