Выражение смешанного произведения через координаты сомножителей

Пусть векторы заданы своими координатами:

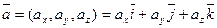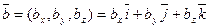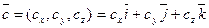, , . Найдем их смешанное произведение, используя формулы для выражения векторного и скалярного произведений:

.

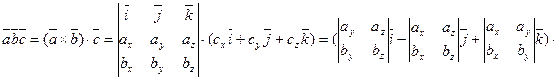
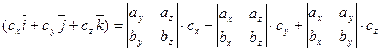Полученную формулу можно записать короче:

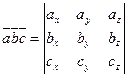
так как правая часть равенства представляет собой разложение определителя третьего порядка по элементам третьей строки.

Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

Приложения смешанного произведения

1. Определение взаимной ориентации векторов в пространстве. Если 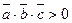,то тройка 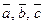— правая; если 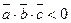, то 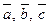- левая тройка.

2. Установление компланарности векторов. Векторы 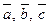компланарны тогда и только тогда, когда их смешанное произведение равно нулю .

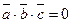3. Объем параллелепипеда и треугольной пирамиды.

Модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах 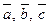, как на сторонах, т.е.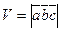 - объем параллелепипеда;

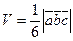- объем пирамиды, построенной на векторах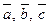

Пример:

По координатам вершин пирамиды 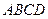найти:

1) косинус угола между ребрам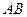и и ;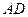

2) площадь треугольника 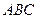- основания пирамиды;

3) объем пирамиды ;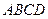

где ; ; ; .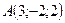

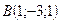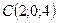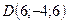Решение:

1) Найдем координаты векторов 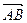и ;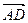

,

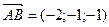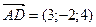
Косинус угола между векторами находится по формуле .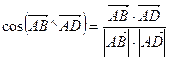

.

, , .

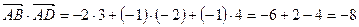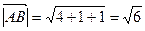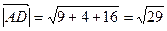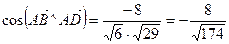Ответ: .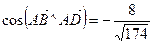

2) площадь треугольника 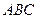вычисляется по формуле:

, ,

,

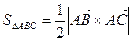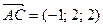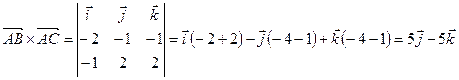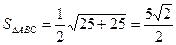
Ответ: 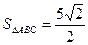кв.ед.

3) Найдем объем пирамиды :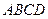

.

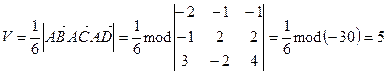Ответ: 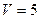куб.ед.