Генераторные измерительные схемы

В датчиках, использующих генераторные измерительные схемы, источники модулирующего сигнала обы­чно строят по схеме синусного генератора. Если ЧЭ входят в состав генератора, то вариации их номиналов под действием измеряемой величины изменяют частоту колебаний генератора. В общем случае, частота генерации соответствует резонансной час­тоте контура, со­стоящего из катушки с индуктивностью L₀ и конденсатора емкостью C₀ соединенных, в зависимости от схемы, последовательно или параллельно. Поскольку на резонансной частоте f₀ сопротивление контура оказывается чисто активным, справедливы следующие выражения:

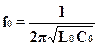- для последовательного колебательного контура и 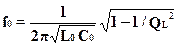- для параллельного. Здесь Q_L - добротность катушки, Q_L = L₀ W₀/R_L; R_L - активное сопротивление катушки, W₀ = 2pf₀. В большинстве случаев Q_L² >> 1, так что для обоих контуров

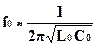
В генераторных измерительных схемах, также и в параметрических, используют различные принципы линеаризации. Чаще всего это сводится к тому, что ЧЭ работают в малой (линейной) зоне, т.е. DL << L₀ и DC << C₀. Тогда в зависимости от типа ЧЭ для соответ­ствующих измене­ний частот f₀ получим соотношения:

Df/f₀ = -DL/2L₀ или Df/f₀ = -DC/2C₀

т.е. f = f₀ (1 - DL/2L₀), или f = f₀ (1 - DC/2C₀).

Пусть измеряемая величина x изменяется относительно значения x₀ по гармоническому закону с частотой w и амплитудой колебаний x ₁, т.е. x(t) = x₀ + x ₁ cos wt. Тогда, как было показано ранее DL(t) = S_L x₁ cos wt. (Аналогично и DC(t) = S_C x₁ cos wt).

В любом случае, мгновенное значение частоты генератора будет равно:

f(t) = f₀ (1 - k x₁ cos wt),

где k = DL/2L₀ или DC/2С₀ в зависимости от типа ЧЭ.

Частота генератора модулируется по закону изменения x(t). Если нас интересует не частота, а выходное напряжение генератора U_вых, то в общем случае для него справедлива запись: U_вых = E sin j (t), где j (t) - мгновенное значение фазы.

Поскольку при модуляции в каждый момент времени dj/dt =W(t) = 2p f(t) то

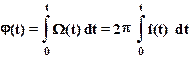
и, следовательно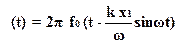

Таким образом, выходной сигнал генератора равен:

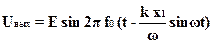
Это выражение может рассматриваться как функция преобразования генераторной схемы. Иногда используют другую запись [ ]:

,

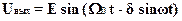где параметр d = k W₀х₁/w - называется коэффициентом частотной модуляции.

Функция преобразования в виде U_вых = G (x) оказывается нелинейной.

Генераторные измерительные схемы часто используются в многоканальных информационных системах (рис. 2.34). В этом случае, сигнал каждого ЧЭ (или датчика в целом) модулирует свою под­несущую частоту. Совокуп­ность промодулированных таким образом сигналов модулирует затем общую несущую частоту W₀.

В заключении рассмотрим особенности частотной характеристики измерительных цепей. Выходной сиг­нал измерительной цепи характеризуется спектром частот, который зависит, во-первых, от спектра частот измеряемой величины, а во-вторых, от возможностей самого информационного канала передать эту величину без искажения. Следовательно, измерительная цепь обладает собственной полосой пропускания В_иц т.е. совокупностью частот, которые могут быть переданы через тракт измерений. Чтобы передать информацию без искажений полоса пропускания измерительной цепи должна быть шире диапазона частот спектра сигнала. Обычно, измеряемую величину х с периодом T представляют в виде ряда Фурье - бесконечной последовательности гармонических составляющих с амплитудами А_n и частотами nf, где n - целое число, f = 1/T - основная частота (первая гармоника) сигнала. Абсолютно точное представление функции х таким рядом требует бесконечно большого числа гармоник (n = ¥) или бесконечно широкой полосы пропускания канала преобразования информации. Ограничение спектра приводит к искажению сигнала; максимальная величина этого искажения определяется числом гармоник, которое сохраняется в процессе преобразования сигнала. Если сигнал можно представить в виде последовательности прямоугольных импульсов длительностью t и периодом T>>t, то допустимая ширина спектра измерительной цепи ~ 1/t [ ]. Например, для t = 1 мкс, верхняя граничная частота спектра преобразователя составит 1 МГц. В соответствии с изложенным, для уменьшения частотных искажений целесообразно использовать измерительные схемы постоянного тока.

7.

Все частотные критерии, в том числе и критерий Михайлова, основаны на хорошо известном из курса высшей математики «Принципа аргумента», который позволяет отобразить необходимое условие устойчивости на частотной плоскости.

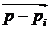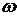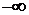Все элементарные вектора изображаются на комплексной плоскости. Задаваясь изменением частоты от до 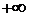будем наблюдать поворот единичных векторов. Анализ их изменения показывает, что устойчивые вектора поворачиваются отлично от неустойчивых. Такое наблюдение позволило сделать четкий вывод о значении угла поворота устойчивой системы в зависимости от числа правых и левых корней (левыми считаются устойчивые корни, а правыми – неустойчивые корни).

Этот частотный критерий устойчивости был сформулирован в 1938 г. советским ученым Михайловым и является интерпретацией принципа аргумента, позволяя судить об устойчивости системы наблюдая за поведением кривой называемой кривой Михайлова.

За основание построения кривой берется характеристический полином вида:

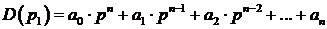
(3.17)

Произведя замену 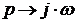получим характеристический полином Михайлова:

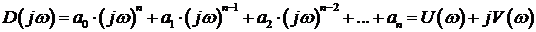(3.18)

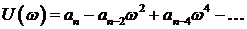
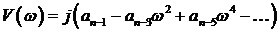
(3.19)

При изменении частоты 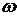вектор 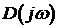будет изменяться как по величине, так и по направлению, описывая своим окончанием некоторую кривую, называемую кривой Михайлова или годографом Михайлова.

Для устойчивых систем кривая Михайлова начинаясь при 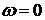на вещественной положительной полуоси, при увеличении частоты 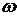, описывает относительно начала координат некую линию.

Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы кривая или годограф Михайлова при изменении 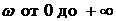начинаясь при 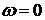на вещественной полуоси, обходила только против часовой стрелки последовательно n-квадрантов комплексной плоскости, нигде не обращаясь в нуль (n – степень характеристического полинома (уравнения)).

Устойчивые САУ:

Неустойчивые САУ:

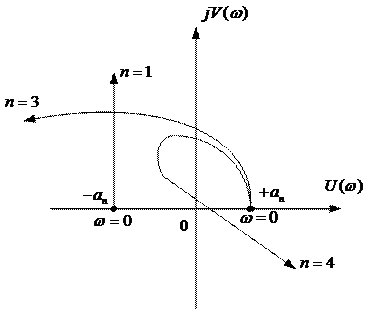
Нейтральные САУ (граница устойчивости):

Анализируя кривую Михайлова можно вывести следствие из него: при прохождении кривой Михайлова числа квадрантов комплексной плоскости, происходит последовательное поочередное пересечение действительной и мнимой соей, т.е.:

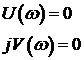
(3.20) (3.21)

Значение частот при которых происходит пересечение кривой с вещественной или мнимой осью, должны является корнями уравнений (3.20) и (3.21), причем 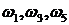корни уравнения (3.21), а 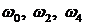- корни уравнения (3.20). При этом корень с большим индексом по значению, также больше корня с меньшим индексом, то обязательно должно выполняться следующее неравенство:

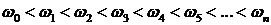
(3.22)

В связи с выше записанным следствие кривой Михайлова можно сформулировать следующим образом: САУ будет устойчивой тогда и только тогда, когда вещественная 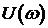и мнимая 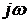функции Михайлова приравненные к нулю, имеют все действительные и перемеживающиеся корни, причем общее число корней равно n и при 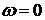выполняется следующее условие:

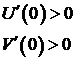
(3.23)

Для реализации этого следствия определяются только корни уравнения 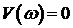. Перемежаемость корней можно проверить подставив в 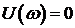найденные корни 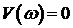. Знаки значений 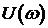при подстановке возрастающих по значению корней должны чередоваться (+ - + - + и т.д.). Если что-то не так – система является неустойчивой.