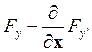Уравнение Эйлера

= 0 (9.10)

или

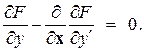(9.10')

В многомерном случае основная задача вариационного исчисления записывается в виде системы n уравнений:

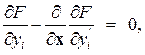i =1: n. (9.10'')

Уравнение (9.10) называется уравнением Эйлера. Оно было найдено Эйлером в 1744г. и играет центральную роль в вариационном исчислении.

Решения уравнения Эйлера называются экстремалями. Только на экстремалях может достигаться экстремум функционала.

Уравнение Эйлера является только необходимым, но не достаточным условием экстремума. Оно не дает гарантии того, что на экстремали действительно достигается экстремум (подобно тому, как в дифференциальном исчислении точки, где y ' = 0, не обязательно доставляют экстремум функции y (t)).

Таким образом, с помощью уравнения Эйлера можно фактически определить функцию, на которой может достигаться экстремум, но не всякое решение уравнения Эйлера является решением поставленной вариационной задачи.

Пример 9.1. Определить функцию, на которой может достигаться экстремум функционала

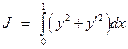
при граничных (краевых) условиях

y (0) = 0, y (1) = 1.

Решение. В рассматриваемом примере F = y ² + y '², поэтому

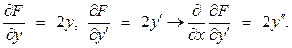
В результате уравнение Эйлера будет иметь вид

y '' – y = 0.

Решение полученного уравнения ищем в виде y = e^rx. В результате получаем уравнение r ² – 1 = 0. Откуда r = ± 1, r ₁ = 1, r ₂ = -1.

В общем виде решение уравнения Эйлера имеет вид

y (х) = С ₁ e^{r 1 x} + С ₂ e^{r 2 x}

или

y (х) = С ₁ e^x + С ₂ e^-х.

Из граничных условий получаем

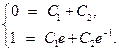
Откуда

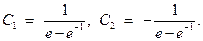
Окончательно, экстремаль имеет вид

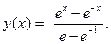
Пример 9.2. Нужно определить кратчайшую линию y (x), соединяющую точки на плоскости – (0;0) и (1;1).

Решение. Длина кривой выражается интегралом

,

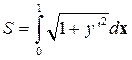т.е. в данном случае 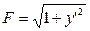; 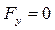, , 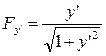и уравнение Эйлера принимает вид:

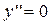, (9.11)

т.е. 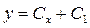, где С и 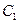– постоянные интегрирования.

Таким, образом, уравнение Эйлера позволило нам определить, что кратчайшим путем, соединяющим две точки на плоскости, может быть только прямая линия. Две произвольные постоянные в формуле (9.11) находятся из условий прохождения линии через две заданные точки.

В данном случае 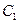= 0; C = 1 и y = x.

Пример 9.3. Найти экстремали функционала

,

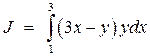удовлетворяющие граничным условиям y (1) = 1, y (3) = 4,5.

Решение. F_y = 3 x -2 y, F_y' = 0.

Уравнение Эйлера имеет вид 3 x -2 y = 0, откуда y (x) = 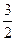x – экстремаль.

Так как найденная экстремаль не удовлетворяет граничному условию y(1) = 1, то вариационная задача решения не имеет.