В формуле 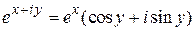 , где x и y - действительные числа, примем х = 0. Получим формулу
, где x и y - действительные числа, примем х = 0. Получим формулу
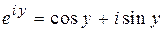 ,
,
которая называется формулой Эйлера.
Используя формулу Эйлера можно любое комплексное число z записать в показательной форме
 ,
,
где r – модуль комплексного числа, а j - его аргумент.
Если в этой формуле Эйлера заменить y на - y, тогда получим 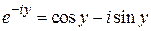 .
.
Решим систему
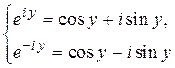
относительно cos y, sin y. Сложим и вычтем уравнения, получим
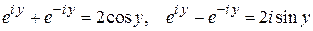 .
.
Отсюда следуют формулы
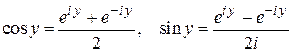 .
.
7.18. Общее решение линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами.
Общее решение неоднородного уравнения, как было показано ранее (теорема 7.4 ), находится как сумма 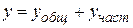 общего решения
общего решения 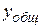 однородного уравнения и частного решения
однородного уравнения и частного решения  неоднородного уравнения, т. е.
неоднородного уравнения, т. е.
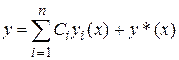 ,
,
где 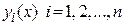 - линейно независимые решения однородного уравнения;
- линейно независимые решения однородного уравнения;
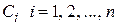 - произвольные постоянные;
- произвольные постоянные;
 - частное решение исходного неоднородного уравнения.
- частное решение исходного неоднородного уравнения.
В общем случае линейное однородное дифференциальное уравнение n -го порядка имеет вид
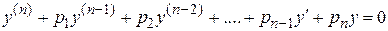 ,
,
где 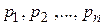 - постоянные величины.
- постоянные величины.
Частные решения однородного уравнения ищут в виде
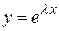 .
.
Производные этой функции равны
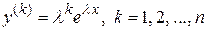 .
.
Подставляем функцию 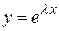 и ее производные в однородное уравнение
и ее производные в однородное уравнение
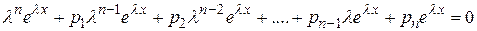 .
.
Делим это уравнение на 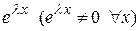 , получаем уравнение
, получаем уравнение
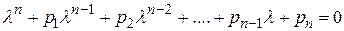 .
.
Данное уравнение называется характеристическим.
Характеристическое уравнение является алгебраическим уравнением n -ой степени относительно l. Любое алгебраическое уравнение n -ой степени имеет в комплексной плоскости n корней.
Рассмотрим все возможные случаи решения однородного дифференциального уравнения в зависимости от вида корней его характеристического уравнения.
Случай 1. Все корни характеристического уравнения 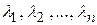 вещественные различные.
вещественные различные.
В этом случае дифференциальное уравнение имеет n линейно независимых частных решений
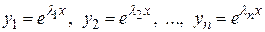 .
.
Общее решение однородного уравнения имеет вид
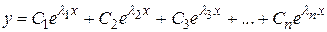
или
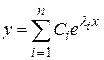 ,
,
где 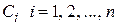 - произвольные постоянные.
- произвольные постоянные.
Пример 7. 22. Найти общее решение уравнения 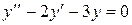 .
.
Составляем характеристическое уравнение
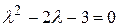 .
.
Находим его корни  . Имеем два частных решения
. Имеем два частных решения 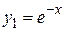 ,
, 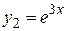 . Записываем общее решение
. Записываем общее решение
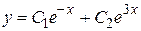 .
.
Случай 2. Характеристическое уравнение имеет пару комплексно-сопряженных корней 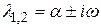 , где
, где  .
.
Тогда этим корням соответствует два линейно независимых комплексно-сопряженных решения
 ,
,
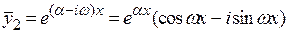 .
.
Из этих решений составляют два линейно независимых действительных решения
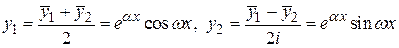 .
.
Общее решение однородного дифференциального уравнения имеет вид
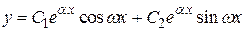 или
или 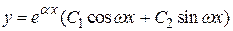 .
.
Пример 7. 23. Найти общее решение уравнения 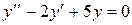 .
.
Составляем характеристическое уравнение
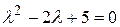 .
.
Находим его корни 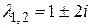 , где
, где  . Уравнение имеет два частных линейно независимых решения
. Уравнение имеет два частных линейно независимых решения
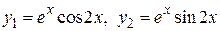 .
.
Записываем общее решение
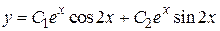 или
или  .
.
Случай 3. Характеристическое уравнение имеет действительный корень l кратности k.
Тогда ему соответствует k линейно независимых частных решения однородного уравнения, которые имеют вид
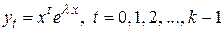 .
.
Общее решение однородного дифференциального уравнения имеет вид
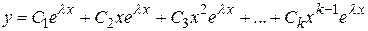 .
.
Пример 7. 24. Найти общее решение уравнения 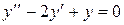 .
.
Составляем характеристическое уравнение
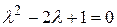 .
.
Оно имеет действительный корень 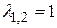 кратности k = 2. Ему соответствует два линейно независимых частные решения
кратности k = 2. Ему соответствует два линейно независимых частные решения 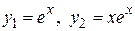 .
.
Общее решение 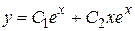 .
.
Случай 4. Характеристическое уравнение имеет пару комплексно-сопряженных корней 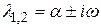 кратности k.
кратности k.
Тогда этим корням соответствует 2 k линейно независимых частных решений однородного уравнения, которые имеют вид
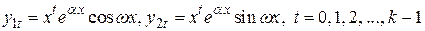 .
.
Общее решение однородного дифференциального уравнения имеет вид
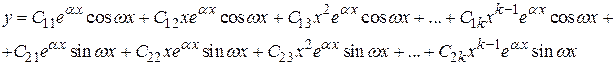
или
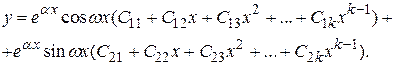
Пример 7. 25. Найти общее решение уравнения
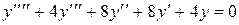 .
.
Составляем характеристическое уравнение и находим его корни.
 Û
Û 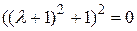 Þ
Þ 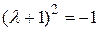 Þ
Þ
 Þ
Þ 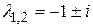 .
.
Уравнение имеет два корня 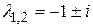 кратности k = 2.
кратности k = 2.
Общее решение уравнения имеет вид
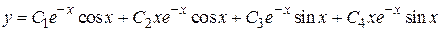 .
.
7.19. Частное решение линейного неоднородного дифференциального уравнения n -ого порядка с постоянными коэффициентами
Вид частного решения неоднородного дифференциального уравнения
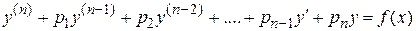
зависит от вида правой части этого уравнения (функции 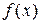 ) и от величин корней характеристического уравнения.
) и от величин корней характеристического уравнения.
Рассмотрим нахождение частного решения для двух видов функции  .
.
Случай 1. Правая часть уравнения
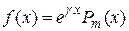 ,
,
где g - вещественное значение, 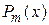 - многочлен m -й степени.
- многочлен m -й степени.
В этом случае частное решение уравнения ищется в виде
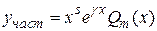
где 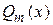 - многочлен m -й степени,
- многочлен m -й степени,
s - степень кратности корня характеристического уравнения 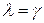 .
.
Если 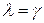 не является корнем характеристического уравнения, то s = 0.
не является корнем характеристического уравнения, то s = 0.
Пример 7. 25. Решить уравнение 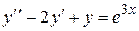 .
.
Характеристическое уравнение однородного уравнения 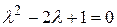 имеет один корень
имеет один корень 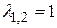 кратности 2. Поэтому общее решение однородного уравнения имеет вид
кратности 2. Поэтому общее решение однородного уравнения имеет вид
 .
.
Находим частное решение неоднородного уравнения. Правая часть уравнения 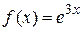 , т. е.
, т. е. 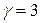 . Данное значение
. Данное значение 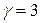 не является корнем характеристического уравнения (следовательно, его кратность s = 0). В этом случае частное решение ищется в виде
не является корнем характеристического уравнения (следовательно, его кратность s = 0). В этом случае частное решение ищется в виде 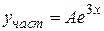 . Находим производные
. Находим производные 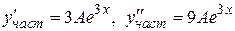 и подставляем их в исходное уравнение
и подставляем их в исходное уравнение
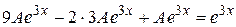 .
.
Делим это уравнение на 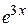 , имеем
, имеем 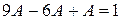 . Отсюда
. Отсюда 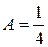 .
.
Записываем частное решение 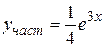 и общее решение
и общее решение
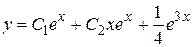 .
.
Пример 7. 26. Решить уравнение  .
.
Общее решение неоднородного уравнения равняется сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения 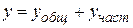 .
.
Найдем общее решение однородного уравнения 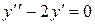 . Его характеристическое уравнение
. Его характеристическое уравнение 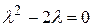 имеет корни
имеет корни 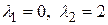 . Общее решение
. Общее решение 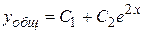 .
.
Найдем частное решение неоднородного уравнения. Правую часть этого уравнения можно представить в виде
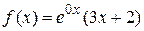 ,
,
где показатель степени g в функции 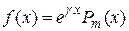 равен g = 0. Это значение совпадает с корнем характеристического уравнения
равен g = 0. Это значение совпадает с корнем характеристического уравнения 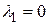 , т. е. является его корнем кратности s = 1. Поэтому частное решение нужно искать в виде
, т. е. является его корнем кратности s = 1. Поэтому частное решение нужно искать в виде
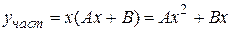 .
.
Находим производные этой функции 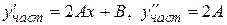 и подставляем их в исходное уравнение. Получаем
и подставляем их в исходное уравнение. Получаем
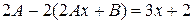 Û
Û 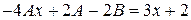 .
.
Приравниваем коэффициенты при одинаковых степенях х (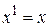 и
и 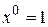 ) в левой и правой частях уравнения
) в левой и правой частях уравнения
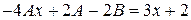
Получаем систему для нахождения коэффициентов A и B
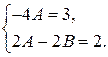
Отсюда 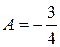 ,
, 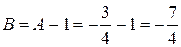 . Записываем частное решение
. Записываем частное решение
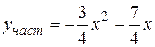 .
.
Общее решение исходного дифференциального уравнения
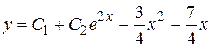 .
.
Случай 2. Правая часть неоднородного дифференциального уравнения имеет вид
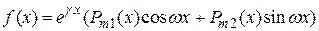 ,
,
где g и w - вещественные значения,
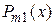 и
и 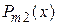 - многочлены степени
- многочлены степени 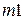 и
и 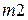 соответственно.
соответственно.
В этом случае частное решение дифференциального уравнения ищется в виде
 ,
,
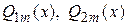 - многочлены степени
- многочлены степени 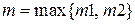 ,
,
s - кратность корня характеристического уравнения 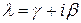 , где
, где 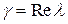 совпадает с числом g в показателе степени
совпадает с числом g в показателе степени 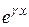 в функции
в функции 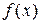 правой части уравнения. Если g в
правой части уравнения. Если g в 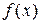 не совпадает с
не совпадает с 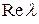 , то s = 0.
, то s = 0.
Пример 7. 27. Решить уравнение  .
.
Характеристическое уравнение 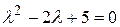 имеет комплексно-сопряженные корни
имеет комплексно-сопряженные корни 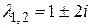 . Поэтому общее решение однородного уравнения
. Поэтому общее решение однородного уравнения 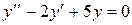 имеет вид
имеет вид
 .
.
Ищем частное решение неоднородного уравнения. Правая часть уравнения 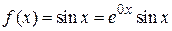 , т. е. g = 0. Значение g = 0 не совпадает с реальной частью корней характеристического уравнения
, т. е. g = 0. Значение g = 0 не совпадает с реальной частью корней характеристического уравнения 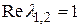 , поэтому s = 0. Частное решение необходимо искать в виде
, поэтому s = 0. Частное решение необходимо искать в виде
 ,
,
где А и В - постоянные величины.
Находим производные  , подставляем их в исходное неоднородное уравнение
, подставляем их в исходное неоднородное уравнение
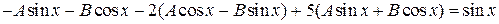 Û
Û
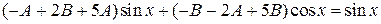 .
.
Приравниваем коэффициенты при sin x и cos x в левой и правой частях этого уравнения. Получаем систему для нахождения постоянных А и В и решаем ее.
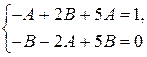 Û
Û 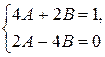 Û
Û 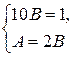 Þ
Þ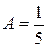 ,
, 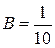 .
.
Записываем частное решение
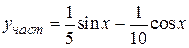
и общее решение
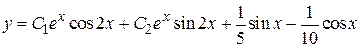 .
.
 2014-02-02
2014-02-02 6022
6022
