Плоские графы

Эйлерова характеристика. Односвязной двумерной клеткой мы будем называть часть поверхности, гомеоморфную единичному кругу D={(x,y): x²+y² £ 1 }.

Теорема 1. Пусть G - граф, разбивающий замкнутую поверхность S на односвязные двумерные клетки. Пусть p - число вершин графа, q – число ребер, r – число клеток. Тогда число p – q + r не зависит от разбивающего графа и называется эйлеровой характеристикой поверхности.

Теорема 2. Пусть G - связный граф, разбивающий сферу на односвяз-ные клетки. Тогда p – q + r = 2.

Доказательство. С помощью индукции по q. Если q=0, то p=1 и r=1. Пусть теорема верна для графа с q ребрами. Докажем ее для q+1 ребер. Рассмотрим два случая добавления ребра:

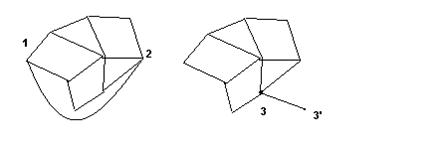
В первом случае добавляется ребро, вершины не добавляются. Во втором добавляется ребро и вершина. Если обозначить новые числа вершин, ребер и граней через p’, q’, r’, то в первом случае получим p’–q’+r’ = p – (q+1)+(r+1) = p–q+r =2, во втором ─ p’–q’+r’ = (p+1) – (q+1)+r = p–q+r =2.