Пример решения задачи 5

Построить дерево по его коду Прюфера 71543 и сделать проверку

Решение.

Выполним распаковку кода Прюфера. С этой целью в верхней строке выпишем заданный код. Под этим кодом выпишем последовательность состоящую из чисел 1, 2, …, m+2, где m – длина кода:

1, 2, 3, 4, 5, 6, 7

7, 1, 5, 4, 3

Положим B={1, 2, 3, 4, 5, 6, 7}. Через a_i обозначим i-й элемент кода. В частности a₁=7, a₂=1, a₃=5 и т.д. Будем выполнять цикл, на каждой итерации которого находится ребро дерево и удаляется элемент из множества B. На i-й итерации цикла, при i = 1, 2, …, m+1, минимальный элемент bÎB, среди не равных никакому из a_j " j ≥ i, соединяется с a_i и затем удаляется из B. Цикл выполняется для i=1, 2, 3, 4, 5. В нашей задаче

При i=1 наименьший из {1, 2, 3, 4, 5, 6, 7} среди не равных {7,1,5,4,3}

равен b=2. Присоединяем ребро {7,2}. Вычеркиваем 2 из верхней последовательности, и 7 – из нижней. B = B\{2} ={1, 3, 4, 5, 6, 7}.

При i=2 наименьший из {1, 3, 4, 5, 6, 7} среди не равных {1,5,4,3}

равен b=6. Присоединяем ребро {1,6}. Вычеркиваем 6 из верхней последовательности, и 1 – из нижней. B = B\{6} ={1, 3, 4, 5, 7}.

При i=3 наименьший из {1, 3, 4, 5, 7} среди не равных {5,4,3}

равен b=1. Присоединяем ребро {5,1}. Вычеркиваем 1 из верхней последовательности, и 5 – из нижней.B = B\{1} ={3, 4, 5, 7}.

При i=4 наименьший из {3, 4, 5, 7} среди не равных {4,3}

равен b=5. Присоединяем ребро {4,5}. Вычеркиваем 5 из верхней последовательности, и 4 – из нижней.B = B\{5} ={3, 4, 7}.

При i=5 наименьший из {3, 4, 7} среди не равных {3}

равен b=4. Присоединяем ребро {3,4}. Вычеркиваем 4 из верхней последовательности, и 3 – из нижней. B = B\{4} ={3, 7}.

Цикл закончился. Соединяем два оставшихся элемента 3 и 7.

Полученное дерево состоит из ребер {7,2}, {1,6}, {5,1}, {4,5}, {3,4}, {3,7}.

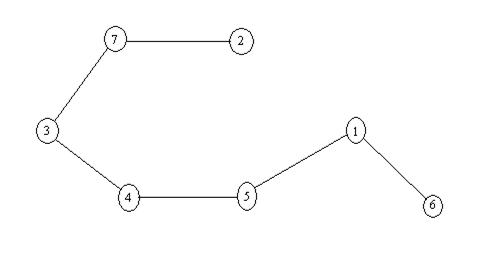
Рис. 2. Дерево с кодом 71543

Сделаем проверку. С этой целью построим код для полученного дерева. Построение кода состоит из цикла, на каждой итерации которого удаляется висячая вершина с наименьшим номером и выписывается номер вершины, соединенной с висячей.

В данном случае удаляем 2 и выписываем 7. Затем удаляем 6 и выписываем 1. Затем удаляем 1 и выписываем 5. Удаляем 5 и выписываем 4. Удаляем 4 и выписываем 3. Цикл заканчивается, когда останется две вершины. В результате получаем код, состоящий из выписанных чисел 7, 1, 5, 4, 3. Этот код совпадает с заданным. Следовательно, дерево построено верно.

Ответ: Дерево состоит из ребер {7,2}, {1,6}, {5,1}, {4,5}, {3,4}, {3,7}.

Задача 6. Моноиды

Задано вещественное число a и подмножество M Í R множества вещественных чисел. Будет ли M относительно операции x*y = x + y + axy моноидом? Группой? Ниже N = {0,1,2,...} обозначает множество натуральных чисел, Q – множество рациональных дробей m/n (где m,n Î Z, n¹0).

Варианты

1. M = [0, 1[, a = –1	19. M = Q, a = ½
2. M = [0, 1[, a = –2	20. M = [0, ½], a = –2
3. M = ]-1, 1[, a = –1	21. M = [0, 5], a = –1/5
4. M = {0, 1}, a = –1	22. M = N, a = 2
5. M = N, a = –1	23. M = R, a = – ½
6. M = R, a = 1	24. M = Q, a = – 1/3
7. M = [0, 1], a = –2	25. M = N, a = 0
8. M = Q, a = 2	26. M = ] –1,0], a = 1
9. M = R \ {1}, a = –1	27. M = ] –1,0], a = 2
10. M = R, a = 2	28. M = ] –1,0], a = 3/2
11. M = R, a = ½	29. M = [0,1], a = – 3/2
12. M = R, a = – ½	30. M = Q, a = ¾
13. M = N, a = –2	31. M = ] –1,0], a = 4/3
14. M = [0, 1[, a = – 1	32. M = R \ {1/2}, a = –2
15. M = Q, a = 0	33. M = [0, 1/3], a = –3
16. M = R, a = – 1	34. M = [0,1], a = – 4/3
17. M = [0, 1], a = – 3/2	35. M = Q, a = 5/6
18. M = Q, a = – 1	36. M = R \ {5/6}, a = - 6/5

Пример решения задачи 6.

Будет ли множество M = [0,1] с операцией x*y = x+y – (9/8)xy полугруппой? Моноидом? Группой?

Решение.

1) Проверим, будет ли x*yÎM при x,y ÎM. Это выполнено если для всех удовлетворяющих неравенствам 0£x, y£1 чисел x, y будет иметь место 0£x*y£1. Рассмотрим произвольный 0£y£1. Функция f(x)= x+y – (9/8)xy при фиксированном y будет линейной по x. На концах интервала [0,1] она принимает значения f(0)=y и f(1)=1-(1/8)y. Поскольку эти значения лежат в интервале [0,1], то значения этой функции во внутренних точках интервала принадлежат [0,1]. Отсюда для всех x,y Î M значения x*y принадлежат M.

2) Проверим ассоциативность (x*y)*z=x*(y*z). С этой целью раскроем обе части проверяемого равенства:

(x+y-(9/8)xy)+z-(9/8) (x+y-(9/8)xy)z = x+(y+z-(9/8)yz)-(9/8)x(y+z-(9/8)yz)

Поскольку последнее равенство имеет место, то операция * ассоциативна. Стало быть, (M,*) – полугруппа.

3) Проверим, будет ли (M,*) моноидом. Напомним, что моноидом называется полугруппа M, в которой существует элемент eÎM, удовлетворяющий для всех xÎM соотношениям x*e = e*x = x.

Этот элемент eÎM называется нейтральным. Для нахождения нейтрального элемента получаем тождество x+e –(9/8)xe = x, которое должно быть выполнено для всех xÎM. Легко видеть, что e=0 удовлетворяет этому тождеству. Отсюда вытекает, что (M,*) – моноид.

4) Проверим, будет ли (M,*) группой. Напомним, что моноид (M,*) называется группой, если для каждого x Î M найдется такой y Î M, что x*y = e. Отсюда данный моноид будет группой, если и только если для каждого xÎ M существует yÎM, удовлетворяющий уравнению x+y-(9/8)xy = 0. Находим y = -x/(1-(9/8)x). Отсюда для x=8/9 это уравнение не имеет решений. Стало быть, заданный моноид не является группой.

Ответ: (M,*) является полугруппой, моноидом, но не является группой