Рассмотрим однородный стержень длины 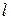 . Будем предполагать, что боковая поверхность стержня теплоизолирована (через поверхность не происходит теплообмена с окружающей средой) и что во всех точках поперечного стержня температура одинакова. Изучим процесс распространения тепла в стержне.
. Будем предполагать, что боковая поверхность стержня теплоизолирована (через поверхность не происходит теплообмена с окружающей средой) и что во всех точках поперечного стержня температура одинакова. Изучим процесс распространения тепла в стержне.
Расположим ось 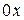 так, что один конец стержня будет совпадать с точкой
так, что один конец стержня будет совпадать с точкой 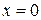 , а другой – с точкой
, а другой – с точкой 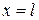 (рис. 3.1).
(рис. 3.1).
Пусть 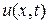 – температура в сечении стержня с абсциссой
– температура в сечении стержня с абсциссой 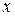 в момент времени
в момент времени 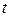 . Скорость распространения тепла, т.е. количество тепла, протекающего через поперечное сечение стержня за момент
. Скорость распространения тепла, т.е. количество тепла, протекающего через поперечное сечение стержня за момент 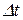 (тепловой поток), пропорционально площади сечения, скорости изменения температуры в направлении, перпендикулярном сечению, и промежутку времени
(тепловой поток), пропорционально площади сечения, скорости изменения температуры в направлении, перпендикулярном сечению, и промежутку времени 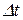 , т.е. определяется формулой:
, т.е. определяется формулой:

Рис. 3.1. К задаче о распространении тепла в стержне
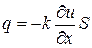 , (3.12)
, (3.12)
где 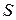 – площадь сечения рассматриваемого стержня;
– площадь сечения рассматриваемого стержня; 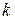 – коэффициент теплопроводности.
– коэффициент теплопроводности.
Знак минус в формуле (3.12) объясняется тем, что величину теплового потока будем считать положительной, когда тепло проходит в сторону возрастания 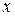 . Если
. Если 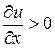 , то это значит, что с возрастанием
, то это значит, что с возрастанием 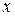 температура повышается, а т.к. тепло переходит от более нагретых участков к менее нагретым, то тепловой поток будет направлен в сторону уменьшения
температура повышается, а т.к. тепло переходит от более нагретых участков к менее нагретым, то тепловой поток будет направлен в сторону уменьшения 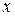 , т.е. его величина будет отрицательной. Будем считать коэффициент теплопроводности постоянным (если стержень однородный и температура меняется в небольших пределах).
, т.е. его величина будет отрицательной. Будем считать коэффициент теплопроводности постоянным (если стержень однородный и температура меняется в небольших пределах).
|
|
|
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами 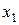 и
и 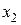 (рис. 3.1), полагая
(рис. 3.1), полагая 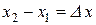 . Составим для него уравнение теплового баланса. Количество тепла, прошедшего через сечение с абсциссой
. Составим для него уравнение теплового баланса. Количество тепла, прошедшего через сечение с абсциссой 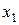 за время
за время 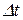 будет равно:
будет равно:
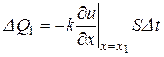 , (3.13)
, (3.13)
то же самое для сечения с абсциссой 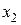 :
:
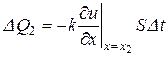 . (3.14)
. (3.14)
Приток тепла 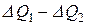 за время
за время 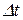 будет равняться:
будет равняться:
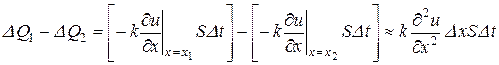 (3.15)
(3.15)
(применили теорему Лагранжа к разности 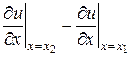 ).
).
Этот приток тепла за время 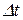 затратился на повышение температуры элемента стержня на величину
затратился на повышение температуры элемента стержня на величину 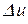 :
: 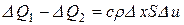 или
или
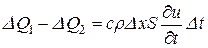 , (3.16)
, (3.16)
где 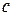 – теплоемкость вещества стержня;
– теплоемкость вещества стержня; 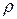 – плотность вещества стержня (
– плотность вещества стержня (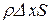 – масса элемента стержня).
– масса элемента стержня).
Приравнивая выражения (3.15) и (3.16) одного и того же количества 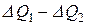 , получим
, получим 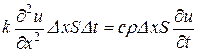 или
или 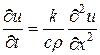 .
.
Обозначая 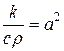 , окончательно получаем:
, окончательно получаем:
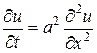 . (3.17)
. (3.17)
Это и есть основное уравнение теплопроводности для однородного стержня без тепловых источников.
Постоянную 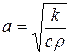 называют коэффициентом температуропроводности. Уравнение (3.17) является однородным и линейным.
называют коэффициентом температуропроводности. Уравнение (3.17) является однородным и линейным.
Предположим, что в некоторых участках стержня может возникнуть или поглощаться тепло (внутри стержня имеются тепловые источники). Выделение (или поглощение) тепла очень удобно характеризовать с помощью плотности тепловых источников. Под плотностью тепловых источников понимают функцию 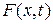 такую, что на малом участке стержня
такую, что на малом участке стержня 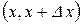 за малый промежуток времени
за малый промежуток времени 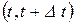 выделяет количество тепла, равное (с точностью до бесконечно малых высшего порядка):
выделяет количество тепла, равное (с точностью до бесконечно малых высшего порядка):
|
|
|
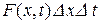 . (3.18)
. (3.18)
Если 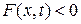 , то тепло не выделяется, а поглощается.
, то тепло не выделяется, а поглощается.
Например, при пропускании через стержень постоянного электрического тока в нем будет выделяться тепло, причем в этом случае 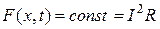 , где
, где 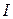 – сила тока;
– сила тока; 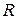 – активное сопротивление единицы длины стержня.
– активное сопротивление единицы длины стержня.
При составлении уравнения теплового баланса 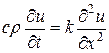 необходимо учесть тепло, возникающее в рассматриваемом участке стержня. Для этого прибавим к правой части данного уравнения величину, определяемую формулой (3.18) и разделенную на
необходимо учесть тепло, возникающее в рассматриваемом участке стержня. Для этого прибавим к правой части данного уравнения величину, определяемую формулой (3.18) и разделенную на 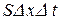 . Получим:
. Получим:
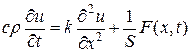 .
.
Разделив обе части равенства на 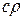 и введя обозначение –
и введя обозначение – 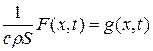 , придем к уравнению:
, придем к уравнению:
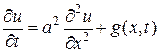 . (3.19)
. (3.19)
Уравнение (3.19) полученное в предположении, что внутри стержня имеются тепловые источники, в отличие от уравнения (3.17) является неоднородным.
Полученные уравнения теплопроводности выведены при условии некоторой идеализации процесса.
Рассмотрим некоторые частные случаи.
1. Если стержень однороден, то 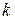 ,
, 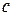 ,
, 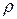 можно считать постоянными и уравнение (3.19) записывают в виде:
можно считать постоянными и уравнение (3.19) записывают в виде:
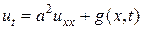 ;
;
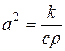 ;
; 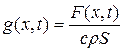 .
.
Если источники отсутствуют, т.е. 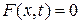 , то уравнение теплопроводности принимает простой вид
, то уравнение теплопроводности принимает простой вид 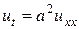 .
.
2. Плотность тепловых источников может зависеть от температуры. В случае теплообмена с окружающей средой, подчиняющегося закону Ньютона, количество тепла, теряемого стержнем, рассчитанное на единицу длины и времени, равно:
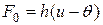 ,
,
где 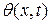 – температура окружающей среды;
– температура окружающей среды; 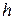 – коэффициент теплообмена. Таким образом, плотность тепловых источников в точке
– коэффициент теплообмена. Таким образом, плотность тепловых источников в точке 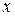 в момент времени
в момент времени 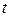 равна:
равна:
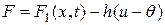 ,
,
где 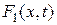 – плотность других источников тепла.
– плотность других источников тепла.
Если стержень однороден, то уравнение теплопроводности с боковым теплообменом имеет следующий вид:
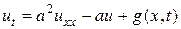 ,
,
где 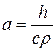 ;
; 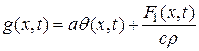 – известная функция.
– известная функция.
3. Коэффициенты 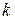 и
и 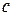 являются медленно меняющимися функциями температуры. Поэтому сделанное выше предположение о постоянстве этих коэффициентов возможно лишь при условии рассмотрения небольших интервалов изменения температуры. Изучение температурных процессов в большом интервале изменения температур приводит к квазилинейному уравнению теплопроводности, которое для неоднородной среды запишется в виде:
являются медленно меняющимися функциями температуры. Поэтому сделанное выше предположение о постоянстве этих коэффициентов возможно лишь при условии рассмотрения небольших интервалов изменения температуры. Изучение температурных процессов в большом интервале изменения температур приводит к квазилинейному уравнению теплопроводности, которое для неоднородной среды запишется в виде:
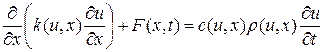 .
.
 2015-03-07
2015-03-07 3135
3135
