Задача ставится так: найти функцию 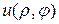 , удовлетворяющую внутри круга
, удовлетворяющую внутри круга 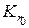 радиуса
радиуса 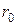 с центром в начале координат уравнению Лапласа:
с центром в начале координат уравнению Лапласа:
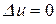 , (4.34)
, (4.34)
непрерывную в замкнутой области 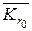 и принимающую заданные значения на границе круга:
и принимающую заданные значения на границе круга:
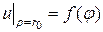 , (4.35)
, (4.35)
где 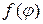 – заданная периодическая функция с периодом
– заданная периодическая функция с периодом 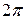 .
.
Из непрерывности решения в 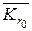 следует его ограниченность в
следует его ограниченность в 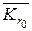 .
.
Уравнение (4.34) в полярных координатах имеет вид:
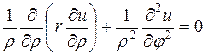 . (4.36)
. (4.36)
Будем искать частные решения уравнения (4.36) в виде:
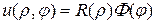 . (4.37)
. (4.37)
Подставляя 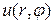 в форме (4.37) в уравнение (4.36), умноженное на
в форме (4.37) в уравнение (4.36), умноженное на 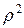 , получим:
, получим:
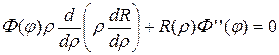 ,
,
или 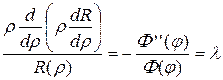 ,
,
откуда получаем два уравнения:
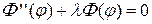 , (4.38)
, (4.38)
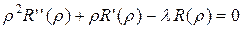 . (4.39)
. (4.39)
Из (4.38) находим 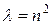
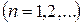 , так что:
, так что:
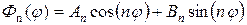 ,
, 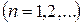 . (4.40)
. (4.40)
А при 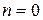 получаем
получаем 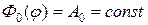 .
.
Уравнение (4.39) является уравнением Эйлера. Полагая в этом уравнении 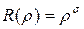 , при
, при 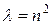 получаем:
получаем:
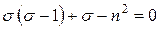 .
.
Отсюда 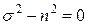 ,
, 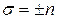
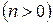 и, следовательно:
и, следовательно:
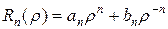 ,
, 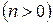 . (4.41)
. (4.41)
При 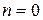 из (4.39) находим:
из (4.39) находим:
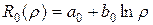 .
.
Так как 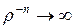 и
и 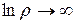 при
при 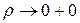 , то для решения внутренней задачи Дирихле нужно положить
, то для решения внутренней задачи Дирихле нужно положить 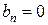 ,
, 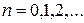 , т.е. взять
, т.е. взять 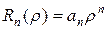 ,
, 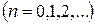 ,
, 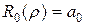 .
.
Решение внутренней задачи Дирихле будем искать в виде ряда:
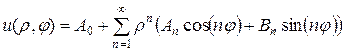 , (4.42)
, (4.42)
где коэффициенты 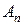 ,
, 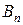 определяются из граничного условия (4.35).
определяются из граничного условия (4.35).
При 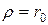 имеем:
имеем:
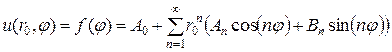 . (4.43)
. (4.43)
Запишем разложение 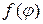 в ряд Фурье:
в ряд Фурье:
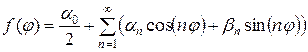 , (4.44)
, (4.44)
где
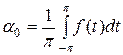 ,
, 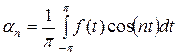 ,
, 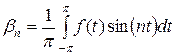 . (4.45)
. (4.45)
Сравнивая ряды (4.43) и (4.44), получаем:
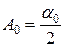 ,
, 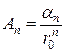 ,
, 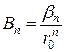 ,
, 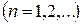 . (4.46)
. (4.46)
Таким образом, формальное решение внутренней задачи Дирихле для круга представимо в виде ряда:
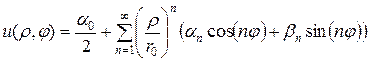 , (4.47)
, (4.47)
где коэффициенты 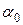 ,
, 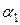 ,
, 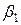 ,…,
,…, 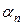 ,
, 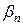 ,… определяются по формулам (4.45).
,… определяются по формулам (4.45).
При 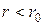 ряд (4.47) можно дифференцировать по
ряд (4.47) можно дифференцировать по 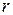 и
и 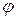 любое число раз, и, значит, функция
любое число раз, и, значит, функция 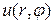 из (4.47) уравняет уравнению
из (4.47) уравняет уравнению 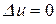 .
.
Решение для внешней задачи Дирихле следует искать в виде ряда:
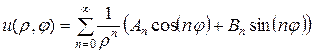 , (4.48)
, (4.48)
где коэффициенты 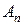 ,
, 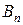 определяются из граничного условия
определяются из граничного условия 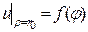 .
.
Для кольцевой области 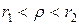 , образованной двумя концентрическими окружностями с центром в точке
, образованной двумя концентрическими окружностями с центром в точке 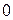 радиусов
радиусов 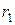 и
и 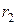 (рис. 4.6), решение задачи ищется в виде ряда:
(рис. 4.6), решение задачи ищется в виде ряда:
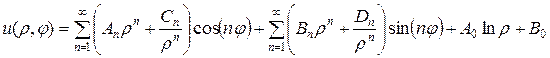 , (4.49)
, (4.49)
коэффициенты которого 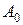 ,
, 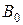 ,
, 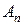 ,
, 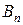 ,
, 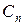 ,
, 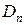 ,
, 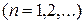 определяются из граничных условий:
определяются из граничных условий:
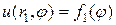 ,
, 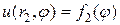 .
.
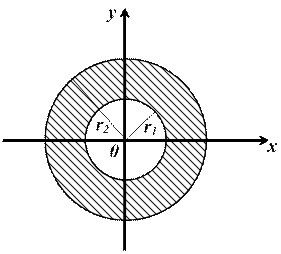
Рис. 4.6. К решению задачи Дирихле для кольца
Пример. Найти решение задачи Дирихле для уравнения Лапласа 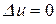 в круге
в круге  , принимающее на границе круга значения
, принимающее на границе круга значения 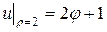 .
.
Решение задачи будем искать в виде ряда:
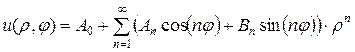 .
.
Найдем коэффициенты ряда по формулам (4.45) и (4.46).
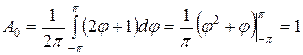 .
.
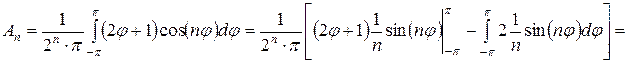
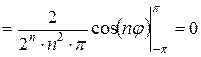 .
.
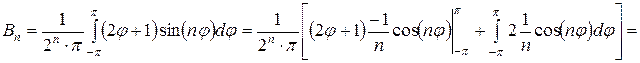
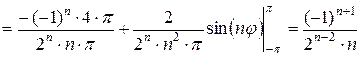 .
.
Итак, получили решение в виде ряда:
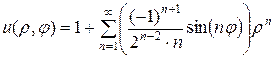 .
.
 2015-03-07
2015-03-07 3493
3493
