Решение краевых задач

Решение краевых задач методом Монте-Карло рассмотрим на примере задачи Дирихле для уравнения Лапласа[3].

Пусть G — односвязная область, на границе которой ¶ G задана функция f = f (Q), Q Î ¶ G. Требуется найти такую функцию u (P), которая внутри области G удовлетворяет уравнению Лапласа:

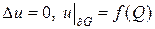. (29)

Построим в области G квадратную сетку с шагом h. Узлы данной сетки делятся на два типа: регулярные и нерегулярные (Лекция №9). Каждый регулярный узел имеет четыре соседних узла P ₁, P ₂, P ₃, P ₄ из области G согласно шаблону, приведенному на рис.7,б из лекции №9. Нерегулярный или граничный узел не имеет ровно четырех соседей из области G.

Составим разностную схему для уравнения Лапласа (29) на квадратной сетке и перепишем полученное уравнение следующим образом:

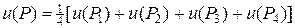. (30)

Для решения конечно-разностной задачи (30) составим следующую теоретико-вероятностную схему. Будем считать, что величина 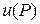пропорциональна плотности неких частиц в узле P. Каждая частица может с вероятностью ¼ за одни шаг по времени перейти в один из четырех соседних узлов: P ₁, P ₂, P ₃, P ₄. Таким образом, частицы, первоначально находящиеся в некотором узле, за один шаг по времени уходят из него, а другие частицы из соседних узлов могут прийти в исходный узел. Считаем, что частица, приходящая на границу области, поглощается.

Вероятность u (P, Q) того, что частица, выйдя из регулярного узла P, окончит блуждание в граничном узле Q, удовлетворяет условию (30), т.е.

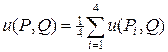(31)

и краевому условию

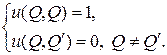(32)

Если промоделировать блуждание частицы по решетке N раз, заставляя каждый раз ее выходить из точки P и подсчитывать количество L ее приходов в точку Q, то отношение 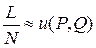является приближенным решением задачи (31) с краевыми условиями (32).

Перейдем к решению задачи Дирихле в общем случае. Пусть, когда частица оказывается в точке Q, с нее берется штраф f (Q). Величина штрафа принимает значения f (Q ₁),…, f (Q_s), где Q ₁,…, Q_s — совокупность всех граничных узлов. Согласно (31), (32), вероятность заплатить штраф f (Q_j) равна u (P, Q_j). Среднее значение штрафа w (P), которое заплатит произвольная частица, выходящая из регулярной точки P, определяется по формуле:

. (33)

Покажем, что выражение (33) удовлетворяет уравнению

.

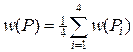Действительно, подставим в (31) вместо Q — Q_j и умножим обе части на f (Q_j), тогда, после суммирования по j, получим уравнение (33). Для граничных узлов функция w (P) удовлетворяет краевым условиям. Так, после подстановки P = Q в (33) согласно (32) пропадут все слагаемые, кроме одного, т.е.

,

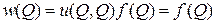т.е. w (P) удовлетворяет конечно-разностному уравнению (30) и принимает на границе заданные значения.

В качестве примера рассмотрим решение уравнения Лапласа u_xx + u_yy = 0 вида:

u = u (x, y) = (x - y)(x + y - 1). (34)

В качестве области интегрирования выберем единичный квадрат, т.е. G (x, y) = [0,1]². Учитывая (34), определим граничные условия для задачи Дирихле

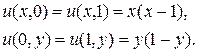(35)

Определим квадратную сетку в единичном квадрате: x_n = h (n -1), y_m = h (m - 1), h = 1/(N - 1), n, m = 1,…, N. Регулярными и нерегулярными (граничными) будут соответственно узлы

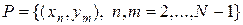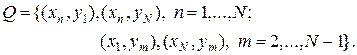, (36)

(36¢)

Найдем решение уравнения Лапласа (34) задачи Дирихле (35) методом Монте-Карло. Разыграем случайный процесс следующим образом. Выберем произвольный регулярный узел P из набора (36). Выпустим из этого узла частицу, и дождемся когда она, путем случайного блуждания, попадет в одну из граничных точек (36¢). Повторим эту процедуру R раз, запоминая число приходов L (P,Q) частицы в граничные точки (36¢). В итоге можно получить следующую расчетную схему:

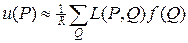. (37)

На листинге_№12 приведен код программы решения уравнения Лапласа (34) для задачи Дирихле в единичном квадрате (35) по расчетной схеме (37).

Листинг_№12

%Программа решения уравнения Лапласа, имеющего

%аналитическое решение (34) для задачи Дирихле

%в единичном квадрате (35) по расчетной схеме

%(37) методом Монте-Карло

function ramble

%Определяем количество N узлов в сетках по

%координатам x и y

N=21; h=1.0/(N-1);

%Определяем сетки по координатам х и у

x=0:h:1; y=0:h:1;

%Вносим краевые условия (35) для задачи Дирихле

for n=1:N

u(n,1)=f(x(n),y(1));

u(n,N)=f(x(n),y(N));

end

for m=1:N

u(1,m)=f(x(1),y(m));

u(N,m)=f(x(N),y(m));

end

%Определяем массив статистических испытаний с

%разной длиной

R=500:500:8000;

%Организуем цикл статистических испытаний с разной

%длиной статистических испытаний

for s=1:length(R)

%Цикл статистических испытаний для каждой

%регулярной точки разностной сетки

for n=2:(N-1)

for m=2:(N-1)

%Определяем четыре массива для

%четырех типов граничных точек

%единичного квадрата: нижнее

%основание, правая сторона,

%верхнее основание, левая

%сторона соответственно

Lx1=zeros(1,(N-1));

LyN=zeros(1,(N-1));

LxN=zeros(1,(N-1));

Ly1=zeros(1,(N-1));

%Статистические испытания длиной R(s)

for r=1:R(s)

Pn=n; Pm=m;

%Цикл, моделирующий случайные

%блужданий на решетке

while (Pn>1)&(Pn<N)&(Pm>1)&(Pm<N)

rnd=rand;

if rnd<=0.25

Pn=Pn+1;

end

if (rnd>0.25)&(rnd<=0.5)

Pm=Pm+1;

end

if (rnd>0.5)&(rnd<=0.75)

Pn=Pn-1;

end

if rnd>0.75

Pm=Pm-1;

end

end

%Подсчет числа приходов частицы с

%координатами (Pn,Pm) в одну из

%граничных точек

if (Pn<N)&(Pm==1)

Lx1(Pn)=Lx1(Pn)+1;

end

if (Pn==N)&(Pm<N)

LyN(Pm)=LyN(Pm)+1;

end

if (Pn>1)&(Pm==N)

LxN(Pn-1)=LxN(Pn-1)+1;

end

if (Pn==1)&(Pm>1)

Ly1(Pm-1)=Ly1(Pm-1)+1;

end

end

%Подсчет решения u(x,y) по формуле (37)

uP=0;

for n1=1:(N-1)

uP=uP+Lx1(n1)*f(x(n1),y(1));

end

for m1=1:(N-1)

uP=uP+LyN(m1)*f(x(N),y(m1));

end

for n1=N:-1:2

uP=uP+LxN(n1-1)*f(x(n1),y(N));

end

for m1=N:-1:2

uP=uP+Ly1(m1-1)*f(x(1),y(m1));

end

u(n,m)=uP/R(s);

end

end

%Сравнение решения, полученного методом

%Монте-Карло u(n,m) с точным решением

%уравнения Лапласа (34)

for n=1:N

for m=1:N

err(n,m)=abs(u(n,m)-(x(n)-y(m))*...

(x(n)+y(m)-1));

end

end

error(s)=max(max(err));

lng(s)=R(s);

end

%Определяем аналитическое решение (34) в ua(n,m)

for n=1:N

for m=1:N

ua(n,m)=(x(n)-y(m))*(x(n)+y(m)-1);

end

end

%Рисуем профиль аналитического решения (34)

subplot(1,2,1); surf(y,x,ua);

%Определяем кривую зависимости ошибки решения

%задачи Дирихле методом Монте-Карло от длины

%статистической серии

subplot(1,2,2); semilogx(lng,error);

%Определяем краевые условия (35)

function z=f(x,y)

z=0;

if (y==0)|(y==1)

z=x*(x-1);

end

if (x==0)|(x==1)

z=y*(1-y);

end

На рис.12 приведен итог работы кода программы листинга_№12. На левой фигуре приведен трехмерный профиль аналитического решения (34) уравнения Лапласа для задачи Дирихле (35). На правой фигуре приведен график зависимости ошибки численного решения задачи Дирихле методом Монте-Карло в зависимости от длины серии статистических испытаний. Отчетливо видна тенденция уменьшения ошибки численного решения по мере роста длины статистической серии.

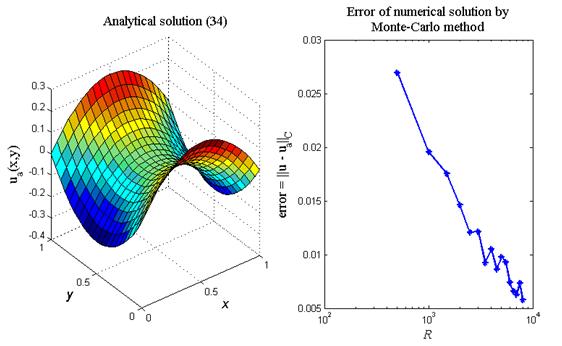
Рис.12. Пример решения краевой задачи (29) методом Монте-Карло

[1] Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 7: программирование, численные методы. — СПб.: БХВ-Петербург, 2005, с.678.

[2] Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах. — М.: Госуд. изд-во физ.-мат. литературы, 1961. 226с.

[3] Бусленко Н.П., Голенко Д.И., Соболь И.М., Срагович В.Г., Шрейдер Ю.А. Метод статистических испытаний (метод Монте-Карло). — М: Госуд. изд-во физ.-мат. литературы, 1962. 331с.