Глава 1. Определение первообразной. Свойства первообразной

Раздел 5. Первообразная и неопределенный интеграл

Глава 1. Определение первообразной. Свойства первообразной.

Операция нахождение производной от функции называется дифференцированием. Обратная дифференцированию операция - отыскание функции по ее производной называется интегрированием.

Функция F (x), производная которой равна функции f (x), т.е.

F ¢(x) = f (x) (1.1)

называется первообразной для f (x).

Так, например, если f (x) = x ⁿ, то ее первообразная есть F (x) = 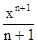, так как

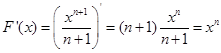Tсли же f (x) = sin (2 x), то ее первообразная

F (x) = - 0.5 cos(2 x),

так как

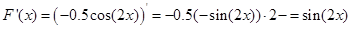Теорема. Пусть F ₁(x) и F ₂(x) две первообразные одной и той же функции f (x) на промежутке [a,b]. Тогда разность между ними есть постоянная величина С.

Доказательство. Обозначим за Ф(х) разность между F ₂(x) и F ₁(x), т.е. Ф(х) = F ₂(x) - F ₁(x) и возьмем производную от функции Ф(х)

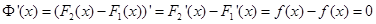(1.2)

Единственной функцией, производная которой при любом значении х равна нулю, есть постоянная величина, следовательно Ф(х) = const ≡ C и

F ₂(x) = F ₁(x) + С. (1.3)

Константа С называется постоянной интегрирования.

Пример. Функция F (x) = – 0.5 cos(2 x) является первообразной не только для f (x) = sin(2x), но и для f(x) = sin(2x) + 4, и для f(x) = sin(2x) - 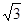, и вообще для любой функции вида sin(2x) + C