Решение. а) Будем искать уравнение прямой с угловым коэффициентом, т.е

а) Будем искать уравнение прямой с угловым коэффициентом, т.е. уравнение вида (4.6). По условию 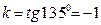. Значит 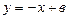. Параметр 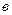найдем из условия принадлежности точки 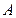искомой прямой. Подставляя координаты точки 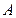в уравнение, получим 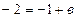, 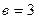. Уравнение искомой прямой имеет вид .

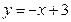б) Уравнение прямой, проходящей через точку 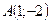параллельно оси 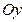имеет вид .

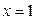в) Чтобы записать уравнение прямой, заданной точкой 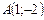и нормальным вектором 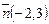, воспользуемся уравнением (4.2):

;

.

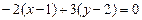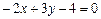г) Используем уравнение (4.3). Полагая 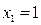, 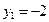; 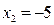, , 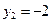получим ;

;

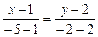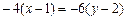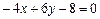или .

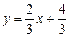Пример 4. Найти уравнение прямой, проходящей через точку :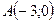

а) параллельно прямой ;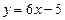

б) перпендикулярно этой же прямой.

Решение. Будем искать уравнение прямой в виде 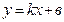. Прямая проходит через точку 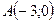, значит 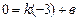, 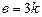. Уравнение искомой прямой приобретает вид: 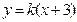. Осталось найти .

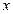а) Если прямая параллельна прямой 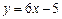, то 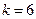, так как угловые коэффициенты параллельных прямых равны (1.8). Значит 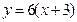или .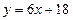

б) Если прямая перпендикулярна прямой 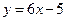, то 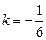по условию (4.9). Значит 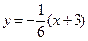или .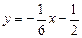

Пример 5. Найти расстояние от точки пересечения двух прямых 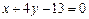и 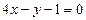до биссектрисы первого координатного угла.

Решение. Найдем точку 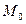пересечения данных прямых. Для этого решим систему по формулам Крамера:

; ;

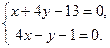
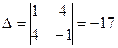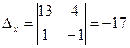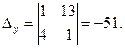
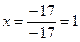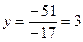; , т.е. .

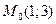По формуле (4.11) находим расстояние 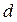до прямо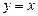й или 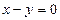- биссектрисы первого координатного угла:

.

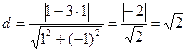Пример 6. Даны вершины треугольника 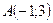, , 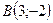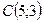. Составить уравнения:

а) стороны ;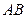

б) медианы, проведенной из вершины ;

в) высоты, опущенной из вершины 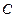на сторону 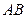. Найти угол между медианой и высотой.