Билет
1)Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Пусть Δ ABC и Так как Так как |
2 билет
1) 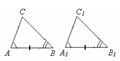 Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство.
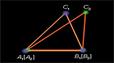
Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, ∠ B = ∠ B1, AB = A1B1.
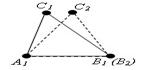 Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
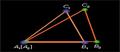
2 Теорема (теорема Чевы). Пусть точки 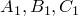 лежат на сторонах
лежат на сторонах 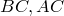 и
и 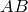 треугольника
треугольника 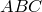 соответственно. Пусть отрезки
соответственно. Пусть отрезки 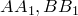 и
и 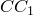 пересекаются в одной точке. Тогда
пересекаются в одной точке. Тогда
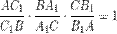 (обходим треугольник по часовой стрелке).
(обходим треугольник по часовой стрелке).
Доказательство. Обозначим через 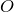 точку пересечения отрезков
точку пересечения отрезков 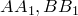 и
и 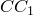 . Опустим из точек
. Опустим из точек 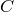 и
и 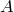 перпендикуляры на прямую
перпендикуляры на прямую 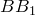 до пересечения с ней в точках
до пересечения с ней в точках 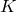 и
и 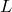 соответственно (см. рисунок).
соответственно (см. рисунок).
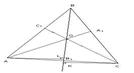 Поскольку треугольники
Поскольку треугольники 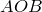 и
и 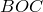 имеют общую сторону
имеют общую сторону 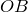 , то их площади относятся как высоты, проведенные на эту сторону, т.е.
, то их площади относятся как высоты, проведенные на эту сторону, т.е. 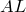 и
и 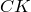 :
:
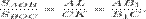 Последнее равенство справедливо, так как прямоугольные треугольники
Последнее равенство справедливо, так как прямоугольные треугольники 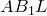 и
и 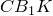 подобны по острому углу.Аналогично получаем
подобны по острому углу.Аналогично получаем
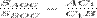 и
и 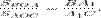 Перемножим эти три равенства:
Перемножим эти три равенства:
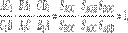 что и требовалось доказать.
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой
Билет
3-ий признак равенства треугольников.
Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
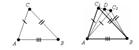 | Дано: ΔАВС, ΔА1В1С1 АВ=А1B1 ВС=В1C1 СА=С1В1 Доказать:ΔАВС=ΔА1В1С1 |
Доказательство:
Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны.
Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку.
Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1.
Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
2)Прямая Эйлера
Прямая Эйлера.
Из доказанных теорем 1 и 2 вытекает интересующее нас свойство замечательных точек треугольника.
Теорема 3. Центр О описанной окружности, центроид G и ортоцентр H любого треугольника лежат на одной прямой, причем точка G лежит между точками О и Н и OG:GH = 1:2.
Доказательство. По теореме 1
3OG = OA + OB + OC.
Сравнивая это равенство с равенством,получим
OH = 3OG.
Следовательно, векторы OH и OG, имеющие общее начало O, расположены на одной прямой и | OG|: |GH| = 1: 2.
Прямая, на которой лежат точки O, G и H, называется прямой Эйлера.
4 билет
1) Теорема синусов
Для произвольного треугольника 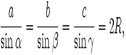 где a, b, c — стороны треугольника, α, β, γ — соответственно противолежащие им углы, а R — радиус описанной около треугольника окружности. где a, b, c — стороны треугольника, α, β, γ — соответственно противолежащие им углы, а R — радиус описанной около треугольника окружности. |
Доказательство:
Достаточно доказать следущие положения:   Проведем диаметр | BG | для описанной окружности. По свойству углов, вписанных в окружность, угол Проведем диаметр | BG | для описанной окружности. По свойству углов, вписанных в окружность, угол 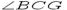 прямой и угол при вершине G треугольника прямой и угол при вершине G треугольника 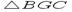 равен либо α, если точки A и G лежат по одну сторону от прямой BC, либо π - α в противном случае. Поскольку sin(π - α) = sinα, в обоих случаях a = 2Rsinα. Повторив тоже рассуждение для двух других сторон треугольника получаем: равен либо α, если точки A и G лежат по одну сторону от прямой BC, либо π - α в противном случае. Поскольку sin(π - α) = sinα, в обоих случаях a = 2Rsinα. Повторив тоже рассуждение для двух других сторон треугольника получаем: 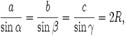 |
2) Каждая сторона треугольника меньше суммы двух других сторон.
Доказательство.
Рассмотрим произвольный треугольник ABC и докажем, что AB<AC+СB. Отложим на продолжении стороны AC отрезок СD, равный стороне СB.
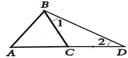 В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB < AD. Но AD = AC + CD = AC + CB, поэтому AB < AC + CB. Теорема доказана.
В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB < AD. Но AD = AC + CD = AC + CB, поэтому AB < AC + CB. Теорема доказана.
Следствие.
Для любых трех точек A, B и С, не лежащих на одной прямой, справедливы неравенства: AB < AC + CB, AC < AB + BC, BC < BA + AC.
Каждое из этих неравенств называется неравенством треугольника
5 билет
1)В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Докажем одну из них
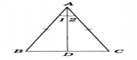 Рис.1Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
Рис.1Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
2) Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 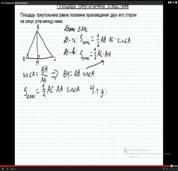 |
Билет
1)
Формулы площади треугольника.
1) Площадь треугольника равна половине произведения основания на высоту.
2) Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
3) Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
4) Площадь треугольника равна произведению трех его сторон, деленному на учетверенный радиус описанной окружности.
5) Формула Герона.
где р - полупериметр треугольника р=(а+b+c)/2
 2015-04-12
2015-04-12 3421
3421

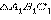 таковы, что
таковы, что 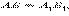
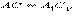
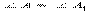 В соответствии с аксиомойсуществует
В соответствии с аксиомойсуществует 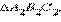 равный данному
равный данному 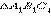 с вершиной
с вершиной 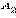 в точке
в точке 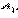 с вершиной
с вершиной 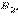 лежащей на луче
лежащей на луче 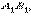 и вершиной
и вершиной 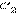 в той же полуплоскости относительно прямой
в той же полуплоскости относительно прямой 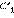 (рис. 4.2.2).
(рис. 4.2.2).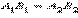 по условию, то на основании точки
по условию, то на основании точки 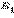 и
и 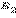 совпадают (рис. 4.2.3).
совпадают (рис. 4.2.3).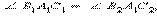 то луч
то луч 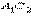 совпадает с лучом
совпадает с лучом 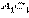 . Так как
. Так как 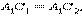 то на основании аксиомы 2.5 вершина
то на основании аксиомы 2.5 вершина 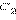 совпадает с вершиной
совпадает с вершиной 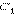 . Тогда
. Тогда 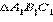 совпадает с
совпадает с 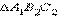 и, значит, равен Δ ABC. Теорема доказана
и, значит, равен Δ ABC. Теорема доказана






