2015-04-12
2673
Предикатом Р в предметной области М называется функция, аргументы которой принимают значения из некоторого множества М, а сама функция – значения 0 (ложь) или 1 (истина):
Р: М ®{0,1}.
Множество М определяется обычно математическим контекстом. Как правило, предикаты обозначаются прописными буквами латинского алфавита (с нижним индексом или без него).
Предикат Р называется n - местным (или предикатом порядка n), если соответствующая функция есть функция от n аргументов. Р (x 1, x 2,…, xn) – предикат n -ого порядка. Если некоторым k аргументам предиката присвоить конкретные значения, то получим предикат, зависящий от (n – k) аргументов. Если все аргументы предиката получают конкретные значения, то имеем 0-местный предикат или высказывание.
Пример. Зададим одноместный предикат R (x) неравенством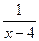 
>3, т. е. положим R (x)=( 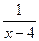>3). Тогда при x =4.04 предикат обращается в истинное высказывание R (x)=1, при х =3 предикат обращается в ложное высказывание, при х =4 R (4) не определено.
Одноместный предикат называют свойством. Например, если m – переменная на множестве натуральных чисел, то S (m)=(для некоторого натурального числа k m =2 k) – свойство четности натуральных чисел.
Заметим, что предикат Р (x 1, x 2,…, xn) определяет n -арное отношение R на множестве М: если Р (x 1, x 2,…, xn)=1, то (x 1, x 2,…, xn) – находятся в отношении R (x 1, x 2,…, xn)Î R), определяемом этим предикатом; если Р (x 1, x 2,…, xn)=0, то (x 1, x 2,…, xn)Ï R.
Каждое уравнение или неравенство с n неизвестными, каждая система уравнений или неравенств с n неизвестными задает соответствующий n -местный предикат. Кроме того, если f (x 1, x 2,…, xn) – произвольная функция, то ей можно сопоставить предикат Р (x 1, x 2,…, xn, y), значение которого для любого набора (a1, a2,…, an, b) значений аргументов x 1, x 2,…, xn, y соответственно определено и равно 1 тогда и только тогда, когда f (x 1, x 2,…, xn) определено и f (а 1, а 2,…, аn) = b. Этот предикат Р (x 1, x 2,…, xn, y) называется предикатом, представляющим функцию f (x 1, x 2,…, xn).
Пусть Р (x 1, x 2,…, xn) – некоторый n -местный предикат, заданный на множестве М, тогда можно определить следующие типы предикатов.
Предикат Р (x 1, x 2,…, xn) называется тождественно истинным, если на любом наборе значений аргументов он обращается в истинное высказывание.
Предикат Р (x 1, x 2,…, xn) называется тождественно ложным, если на любом наборе значений аргументов он обращается в ложное высказывание.
Предикат Р (x 1, x 2,…, xn) называется выполнимым, если существует хотя бы один набор значений аргументов, на котором он обращается в истинное высказывание.
Каждый рассматриваемый предикат является или тождественно истинным, или тождественно ложным, или выполнимым. Для выполнимого предиката множество значений аргументов, на котором он обращается в истинное высказывание, называется множеством истинности предиката и обозначается Ep.
Говорят, что набор (а 1, а 2,…, аn)Î М удовлетворяет предикату Р (x 1, x 2,…, xn), если при подстановке значений из этого набора вместо аргументов предиката он обращается в истинное высказывание.
Пусть Р1 (x 1, x 2,…, xn) и Р2 (x 1, x 2,…, xn) – два n -местных предиката, заданных на одном и том же множестве М. Предикат Р2 (x 1, x 2,…, xn) называется следствием предиката Р1 (x 1, x 2,…, xn), если любой набор, удовлетворяющий Р1 (x 1, x 2,…, xn), удовлетворяет и Р2 (x 1, x 2,…, xn).
Пример. Определим на множестве натуральных чисел одноместные предикаты R (n)=«n делится на 6» и Q (n)=«n делится на 3». Тогда Q (n) является следствием R (n), но не наоборот, так как Q (9)=1, R (9)=0.
Из этого определения следует, что любой предикат на данном множестве есть следствие тождественно ложного предиката на этом множестве; тождественно истинный предикат на данном множестве есть следствие любого предиката на этом множестве.
Пусть Р1 (x 1, x 2,…, xn) и Р1 (x 1, x 2,…, xn) – два n -местных предиката, заданных на одном и том же множестве М. Эти предикаты называются равносильными, если их значения для любого набора значений переменных совпадают. Этот факт обозначается Р1 (x 1, x 2,…, xn)º Р2 (x 1, x 2,…, xn) и читается «Р1 (x 1, x 2,…, xn) равносильно Р2 (x 1, x 2,…, xn)».
Пример. Равносильные уравнения, неравенства, системы уравнений или неравенств равносильные предикаты.
При выявлении равносильности двух предикатов, заданных на одном и том же множестве, используется следующая теорема (доказательство в [3]):
Предикаты Р1 (x 1, x 2,…, xn) и Р2 (x 1, x 2,…, xn), заданные на множестве M, равносильны тогда и только тогда, когда каждый из ни есть следствие другого.
Над предикатами можно производить обычные логические операции, в результате которых получают новые предикаты, при этом приоритет операций остается тем же. Кроме операций логики высказываний для предикатов существуют специальные операции – операции навешивания кванторов. Предикаты, содержащие кванторы, называются кванторными предикатами.
Пусть Р (х) – предикат, заданный на множестве М.
Под выражением " хР (х) будем понимать высказывание, принимающее значение 1, если для каждого элемента х Î М Р (х) обращается в истинное высказывание, и 0 – иначе.
Под выражением $ хР (х) будем понимать высказывание, принимающее значение 1, если существует элемент х Î М, такой что Р (х) является истинным высказыванием, и 0 – в противном случае.
Символы " и $ называются соответственно квантором всеобщности и квантором существования. В выражениях " хР (х) и $ хР (х) Р (х) называется областью действия квантора.
Заметим, что квантор всеобщности можно рассматривать как обобщение конъюнкции:
Если М ={ x 1, x 2,…, xn }, то " хР (х)º Р (x 1)Ù Р (х 2)Ù…Ù Р (хn),
а квантор существования – как обобщение дизъюнкции: если
М ={ x 1, x 2,…, xn }, то $ хР (х)º Р (x 1)Ú Р (х 2)Ú…Ú Р (хn).
Для бесконечных предметных областей кванторы играют роль бесконечных конъюнкций и дизъюнкций.
Квантор существования является двойственным по отношению к квантору всеобщности и наоборот.
Навешивание квантора на n -местный предикат приводит к уменьшению местности на 1. Таким образом, если Р (x 1, x 2,…, xn) – n -местный предикат, то " xi Р (x 1, x 2,…, xn) и $ xi Р (x 1, x 2,…, xn) – (n –1)-местные предикаты. Переменная, следующая за квантором, называется связанной (от нее кванторный предикат не зависит), иначе переменная называется свободной. Таким образом, существует два способа образования высказываний на основе предикатов: замещение в предикате всех переменных значениями из предметных областей и навешивание на предикаты кванторов.
Рассмотрим некоторые свойства операций навешивания кванторов.
1. Одноименные кванторы можно менять местами:
" x " y P (x, y)º" y " x P (x, y); $ x $ y P(x, y)º$ y $ x P (x,y).
2. При отрицании кванторного предиката знак отрицания относится к внутреннему предикату, а квантор меняется на двойственный: существование на всеобщность и наоборот:
;
.
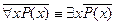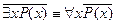Это свойство распространяется и на предикаты с несколькими кванторами.
Пример. Ответим на вопрос: «Какой четырехугольник не является параллелограммом?» (дадим определение «не параллелограмма»).
Запишем одно из определений параллелограмма (x, y –стороны четырехугольника)
$ x $ y ((x ½½ y)Ù(x = y)).
Тогда параллелограммом называется четырехугольник, у которого
,
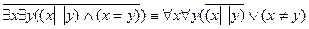то есть четырехугольник не является параллелограммом, если каждые две его стороны или не параллельны, или не равны.
Таким образом, данное правило удобно для построения отрицательных математических предложений.
3. Пусть Р (x 1, x 2,…, xn) – n -местный предикат, тогда " xiР (x 1, x 2,…, xn) – (n –1)-местный предикат, который на наборе (a1, a2,…, ai-1, ai+1,..., an) принимает значение 1 тогда и только тогда, когда одноместный предикат
Р (a1, a2,…, ai-1, хi, ai+1,..., an) является тождественно истинным.
Замечание. Если Р (х) – одноместный предикат, то выражение " хР (х) называется универсальным высказыванием, соответствующим одноместному предикату Р (х). Универсальное высказывание " хР (х) истинно, если одноместный предикат Р (х) тождественно истинный, и ложно в противном случае.
4. Пусть Р (x 1, x 2,…, xn) – n -местный предикат, тогда $ xiР (x 1, x 2,…, xn) – (n –1)-местный предикат, который на наборе (a1, a2,…, ai-1, ai+1,..., an) принимает значение 1 тогда и только тогда, когда одноместный предикат Р (a1, a2,…, ai-1, хi, ai+1,..., an) является выполнимым.
Замечание. Если Р (х) – одноместный предикат, то выражение $ хР (х) называется экзистенциональным высказыванием, соответствующим одноместному предикату Р (х). Экзистенциональное высказывание $ хР (х) истинно, если одноместный предикат Р (х) выполнимый, и ложно, если он тождественно ложный.
Пример. Определить значение высказывания $ y " х (х нацело делится на y) на множестве целых чисел.
Заметим, что " х (х нацело делится на y) = S (y) – одноместный предикат. S (1)=1, так как предикат (х нацело делится на 1) является тождественно истинным. S (4)=0, так как предикат (х нацело делится на 4) выполнимый. Следовательно, существует набор (х =1), на котором предикат S (y) обращается в истинное высказывание, и набор (х =4), на котором предикат обращается в ложное высказывание, поэтому предикат S (y) является выполнимым, а $ y " х (х нацело делится на y) истинным высказыванием, так как квантор существования навешивается на выполнимый предикат.
5. (n –1)-Местный предикат " xiР (x 1, x 2,…, xn) на некотором множестве является тождественно-истинным тогда и только тогда, когда n -местный предикат Р (x 1, x 2,…, xn) на этом множестве тождественно истинный.
6. (n –1)-Местный предикат $ xiР (x 1, x 2,…, xn) на некотором множестве является тождественно-ложным тогда и только тогда, когда n -местный предикат Р (x 1, x 2,…, xn) на этом множестве тождественно ложный (доказательство этого свойства в [3]).
Пример. Пусть на множестве натуральных чисел заданы предикаты
(
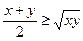) и (x+y<0),
первый из которых тождественно-истинный, а второй – тождественно ложный. По свойствам 5 и 6 можно заключить, что
" х (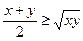), " y (
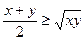) – тождественно истинные одноместные предикаты;
" x (x + y <0); " y (x + y <0) – тождественно ложные одноместные предикаты.
Кванторные предикаты используются для записи различных высказываний.
Пример. Запишем на языке предикатов высказывание «Любые два действительных числа либо равны, либо одно из них меньше другого». Введем в рассмотрение следующие предикаты:
D (x)= «х есть действительное число»;
R (x,y)= «x = y»; P 1(x, y)= «x > y»; P 2(x,y)= «x < y».
Наше высказывание запишется в виде:
" x " y (D (x)Ù D (y)® R (x)Ú P 1(x,y)Ú P 2(x,y))
или
" x " y (D (x)Ù D (y)® (x = y)Ú(x > y)Ú(x < y).
Замечание. Для записи на языке предикатов данных высказываний не существует особых правил. В каждом конкретном случае нужно пытаться передать смысл высказывания с помощью символов языка предикатов.
