При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других. Ее изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в последние десятилетия в экономических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений, называемых также структурными уравнениями.
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная 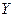 рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов 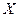 :
:
|
|
|
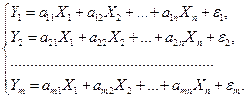
Набор факторов 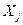 в каждом уравнении может варьировать. Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки
в каждом уравнении может варьировать. Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки 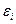 .
.
Если зависимая переменная 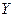 одного уравнения выступает в виде фактора
одного уравнения выступает в виде фактора 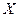 в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
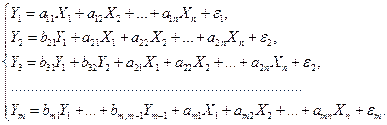
В данной системе зависимая переменная 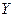 включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов
включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов 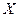 . Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
. Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях – в правую часть системы:
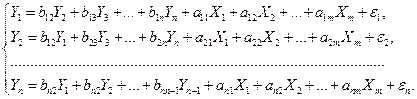 (6.1)
(6.1)
Система уравнений в виде (6.1) называется структурной формой модели (СФМ).
Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.
|
|
|
Переменные 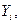
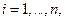 определяемые из модели (6.1), называются эндогенными (внутренними, зависимыми) переменными. Переменные
определяемые из модели (6.1), называются эндогенными (внутренними, зависимыми) переменными. Переменные 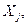
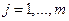 . задаваемые извне, называются экзогенными (внешними).
. задаваемые извне, называются экзогенными (внешними).
Совокупность экзогенных переменных, а также прошлых (лаговых) значений эндогенных переменных называют предопределенными переменными, т.е. предопределенные переменные – это известные в текущий момент времени 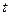 переменные.
переменные.
Коэффициенты 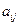 и
и 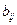 называются структурными коэффициентами модели.
называются структурными коэффициентами модели.
Структурная форма модели, преобразованная к виду, когда зависимые (эндогенные) переменные входят только в левые части, называется приведенной формой модели (ПФМ):
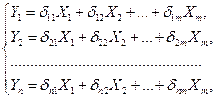 (6.2)
(6.2)
где 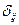 – коэффициенты ПФМ.
– коэффициенты ПФМ.
Примером системы взаимосвязанных уравнений является модель динамики цены и зарплаты:
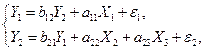
где  – темп изменения месячной зарплаты,
– темп изменения месячной зарплаты,
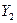 – темп изменения цен,
– темп изменения цен,
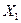 – уровень безработицы,
– уровень безработицы,
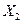 – темп изменения постоянного капитала,
– темп изменения постоянного капитала,
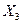 – темп изменения цен на импорт сырья.
– темп изменения цен на импорт сырья.
Пример. Преобразование структурной формы модели к приведенной форме модели. Преобразовать СФМ
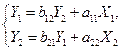
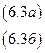
к ПФМ
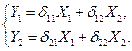
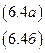
Выражая 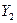 из (6.3 а)
из (6.3 а)
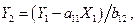 (6.5)
(6.5)
приравнивая правые части (6.5) и (6.3 б) и разрешая результат относительно 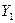 , находим уравнение (6.4 а):
, находим уравнение (6.4 а):
. 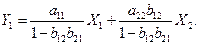
Аналогично, находя 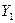 из (6.3 б)
из (6.3 б)
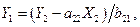 (6.6)
(6.6)
приравнивая правые части (6.6) и (6.3 а) и разрешая результат относительно 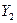 , находим уравнение (6.4 б):
, находим уравнение (6.4 б):
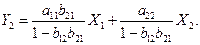
Таким образом,
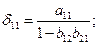
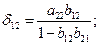
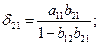
 2015-04-01
2015-04-01 2928
2928
