В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 0 и 1. В дальнейшем переменные будем обозначать латинскими буквами х, у, z,.... В алгебре логики определено отношение эквивалентности (=) и три операции: дизъюнкция (операция ИЛИ), обозначаемая знаком V (+); конъюнкция (операция И), обозначаемая точкой, которую можно опускать (например, х·у=ху); отрицание (инверсия, операция НЕ), обозначаемое чертой над переменными или элементами 0 и 1 (например, 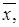
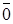 ,
, 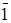 ). Отношение эквивалентности удовлетворяет следующим свойствам: х = х -рефлексивность; если х = у, то у = х - симметричность; если х = у и у = z, то x = z - транзитивность. Из отношения эквивалентности следует принцип подстановки: если х = у, то в любой формуле, содержащей х, вместо х можно подставить у, и будет получена эквивалентная формула.
). Отношение эквивалентности удовлетворяет следующим свойствам: х = х -рефлексивность; если х = у, то у = х - симметричность; если х = у и у = z, то x = z - транзитивность. Из отношения эквивалентности следует принцип подстановки: если х = у, то в любой формуле, содержащей х, вместо х можно подставить у, и будет получена эквивалентная формула.
Алгебра логики определяется следующей системой аксиом:
| х = 0, если х ≠ 1 х = 1, если х ≠ 0 | (4.30) |
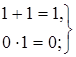 | (4.31) |
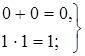 | (4.32) |
 | (4.33) |
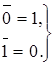 | (4.34) |
Аксиома (4.30) утверждает, что в алгебре логики рассматриваются только двоичные переменные, аксиомы (4.31) - (4.33) определяют операции дизъюнкции и конъюнкции, а аксиома (4.34) - операцию отрицания. Если в аксиомах (4.31) - (4.34), заданных парами, произвести взаимную замену операций дизъюнкции и конъюнкции, и также элементов 0 и 1, то из одной аксиомы пары получится другая. Это свойство называется принципом двойственности.
С помощью аксиом алгебры логики можно доказать целый ряд теорем и тождеств. Одним из эффективных методов доказательства теорем является метод перебора всех значений переменных. Если теорема истинна, то с учетом (4.31) - (4.34) при подстановке любых значений переменных в обе части выражения, формулирующего утверждение теоремы, должно получиться тождество. Метод перебора не слишком трудоемок, так как переменные могут иметь только два значения: 0 и 1. Так, методом перебора легко убедиться в справедливости следующих теорем:
коммутативные законы
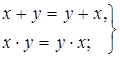 | (4.35) |
ассоциативные законы
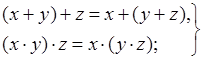 | (4.36) |
дистрибутивные законы
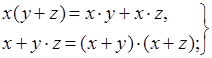 | (4.37) |
законы двойственности (теоремы де Моргана)
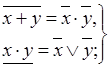 | (4.38) |
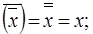 | (4.39) |
законы поглощения
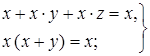 | (4.40) |
операции склеивания
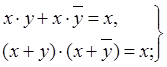 | (4.41) |
операции обобщенного склеивания
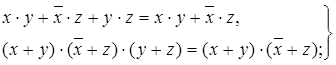 | (4.42) |
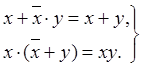 | (4.43) |
Если в логическое выражение входят операции дизъюнкции и конъюнкции, то следует соблюдать порядок выполнения операций: сначала выполняется операция конъюнкции, а затем операция дизъюнкции. В сложных логических выражениях для задания порядка выполнения операций используются скобки.
Некоторые теоремы и тождества алгебры логики имеют особое значение, так как позволяют упрощать логические выражения. Например, в соотношениях (4.10) - (4.13), (4.40) - (4.43) правая часть проще левой. Поэтому, произведя в логических выражениях соответствующие преобразования, можно добиться существенного их упрощения. Особенно часто для преобразования логических выражений, с целью их упрощения, используются тождества (4.40) - (4.43).
Операция сумма по модулю два (исключающее ИЛИ, логическая неравнозначность) обозначается символом Å и определяется соотношением:
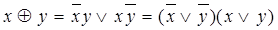 . . | (4.44) |
Используя аксиомы алгебры логики (4.30) - (4.34), легко убедиться, что:
0 Å 0 =1 Å 1 = 0; 0 Å 1 = 1 Å 0 = 1. (4.45)
Из соотношений следует, что значение х Å у совпадает со значением младшего разряда суммы двух двоичных чисел, где х и у - значения младших разрядов этих чисел. Соответственно этому значение i -ro разряда суммы двух двоичных чисел будет определяться значением xi Å yi Å zi; где xi и yi - значения i -x разрядов двоичных чисел, a z i - перенос в i -й разряд из предыдущего
(i − 1)-го разряда.
Операция сумма по модулю два коммутативна, ассоциативна и дистрибутивна относительно операции конъюнкции, т. е.
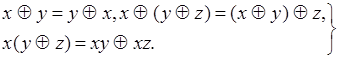 | (4.50) |
Для операции сумма по модулю двасправедливы также следующие тождества:
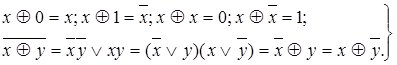 | (4.51) |
 2015-04-01
2015-04-01 4760
4760
