1.2.1 Определение начальных значений и составление характеристических уравнений.
Задача 1.1 Решение: Определить независимые и зависимые начальных условий для электрической цепи (см. рисунок 1.1).Независимые начальные условия определяют по второму закону коммутации по схеме до коммутации (см. рисунок 1.2).
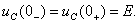 (1.8)
(1.8)
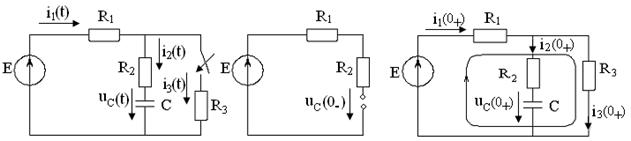
Рисунок 1.1 Рисунок 1.2 Рисунок 1.3
Зависимые начальные условия находят для цепи после коммутации (см. рисунок 1.3), записав уравнения в соответствии с законами Кирхгофа:
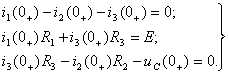 (1.9)
(1.9)
Выразим из первого уравнения системы уравнений (1.9) 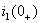 и подставим во второе уравнение. С учетом того, что
и подставим во второе уравнение. С учетом того, что 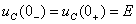 , получим:
, получим:
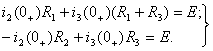 (1.10)
(1.10)
Решая систему уравнений (1.10), определим зависимые начальные условия 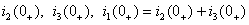 .
.
Задача 1.2 Длясхемы(см. рисунок 1.4) составить характеристическое уравнение и определить его корень: а) по однородному дифференциальному уравнению;
б) по методу входного сопротивления; в) определить корень по постоянной времени цепи 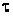 .
.

Рисунок 1.4 Рисунок 1.5 Рисунок 1.6
Решение: а) Составим характеристическое уравнение по однородному дифференциальному уравнению. Запишем неоднородное дифференциальное уравнение относительно тока 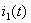 :
: 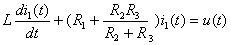 ,
,
|
|
|
приравняем к нулю правую часть неоднородного уравнения, получим однородное дифференциальное уравнение: 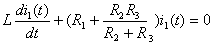 .
.
Заменим 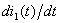 на р,
на р, 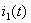 на 1, получим характеристическое уравнение:
на 1, получим характеристическое уравнение:
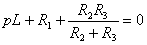 , (1.11)
, (1.11)
отсюда корень характеристического уравнения
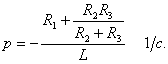 (1.12)
(1.12)
б) Составление характеристического уравнения по методу входного сопротивления. Перейдём от заданной схемы цепи после коммутации к комплексной схеме (рис. 1.5) и запишем комплексное входное сопротивление
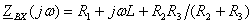 , заменим
, заменим 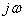 на р, выражение
на р, выражение 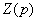 приравняем к нулю и получим характеристическое уравнение:
приравняем к нулю и получим характеристическое уравнение:
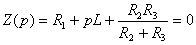 , (1.13)
, (1.13)
корень которого вычисляется по формуле (1.12).
в) Определить корни по постоянной времени цепи 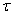 .
.
Известно, что 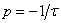 . Для цепи с одним индуктивным элементом постоянная времени
. Для цепи с одним индуктивным элементом постоянная времени 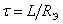 . Эквивалентное сопротивление цепи
. Эквивалентное сопротивление цепи 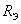 определяется относительно зажимов реактивного элемента (индуктивности), при этом
определяется относительно зажимов реактивного элемента (индуктивности), при этом
необходимо закоротить входной источник ЭДС (см. рисунок 1.6): 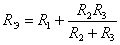 .
.
1.2.2 Расчёт переходных процессов в цепях первого порядка.
Задача 1.3 Накопительная емкость импульсного модулятора передающего устройства РЛС (см. рисунок 1.7, а) после включения разряжается через разрядное сопротивление. Определить время, через которое напряжение на емкости уменьшится до уровня U = 20 В, если U0= 20 кВ, С = 5 мкФ, разрядное сопротивление Rp = 10 кОм.
Решение: Конденсатор заряжен до напряжения 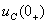 =U0=20 кВ. Составим дифференциальное уравнение по второму закону Кирхгофа для цепи после коммутации (см. рисунок 1.7,б):
=U0=20 кВ. Составим дифференциальное уравнение по второму закону Кирхгофа для цепи после коммутации (см. рисунок 1.7,б):
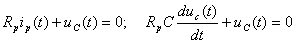 (1.14)
(1.14)
где 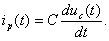
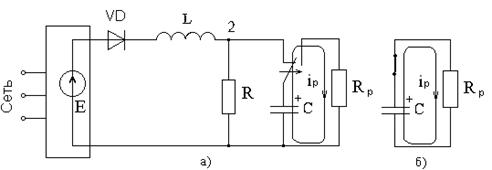
Рисунок 1.7
Решением дифференциального уравнения (1.14) является переходное напряжение на емкости, которое имеет вид
|
|
|
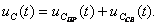
Принуждённая составляющая напряжения 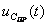 (для схемы после коммутации (см. рисунок 1.7,б) при
(для схемы после коммутации (см. рисунок 1.7,б) при 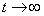 ) равна нулю:
) равна нулю:
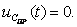
Свободная составляющая напряжения:
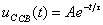 B.
B.
И переходное напряжение будет равно: 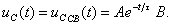
Определим постоянную времени цепи 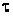 , используя соотношение
, используя соотношение
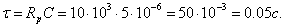
Определим постоянную интегрирования Аиз начальных условий (при 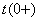 ).
).
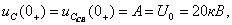
Напряжение на ёмкости в переходном режиме будет равно:
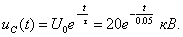 (1.15)
(1.15)
Вычислим время разряда накопительной емкости до U = 20 В из уравнений:
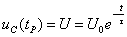 или
или 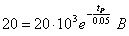 отсюда
отсюда 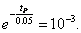
После логарифмирования получаем:
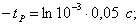
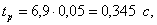
таким образом, время разряда накопительной емкости до U = 20 В составляет примерно 7τ.
График напряжения на емкости 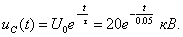 построен в среде Mathcad (см. рисунок 1.8).
построен в среде Mathcad (см. рисунок 1.8).
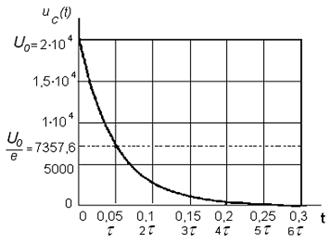
Рисунок 1.8
Вывод. Для регулирования длительности переходного процесса необходимо изменять в цепи постоянную времени 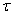 . Это достигается путем выбора параметров R и С. За время
. Это достигается путем выбора параметров R и С. За время 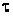 свободная составляющая уменьшается в е = 2,718 раз.
свободная составляющая уменьшается в е = 2,718 раз.
Задача 1.4 Интегрирующая цепь (см. рисунок 1.9) с параметрами R1 = 30 Ом, R2 = 20 Ом, С = 50 мкФ, Е = 100 В подключается к сопротивлениюR2.
Определить закон изменения напряжения на конденсаторе и токов в ветвях в переходном режиме.
Решение: Определяют независимые начальные условия 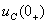 . Из эквивалентной схемы для
. Из эквивалентной схемы для 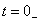 (см. рисунок 1.10) находят
(см. рисунок 1.10) находят 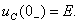
Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации:
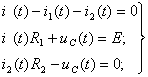 (1.16)
(1.16)
Переходное напряжение 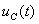 является решением ддифференциальных уравнений и представляется в виде:
является решением ддифференциальных уравнений и представляется в виде: 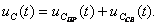

Рисунок 1.9 Рисунок 1.10 Рисунок 1.11
Определяют принуждённую составляющую напряжения 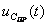 в установившемся режиме цепи после коммутации
в установившемся режиме цепи после коммутации 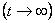 из схемы (см. рисунок 1.11):
из схемы (см. рисунок 1.11):
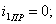
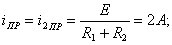
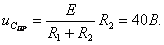
Определяют свободную составляющую напряжения 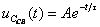 .
.
Постоянная времени цепи 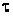 находится по формуле:
находится по формуле:
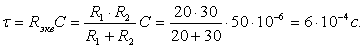 (1.17)
(1.17)
Постоянную интегрирования определяют по начальному значению напряжения 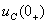 :
: 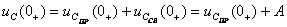 , отсюда
, отсюда
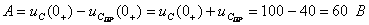 .
.
Записывают аналитические выражения для переходного напряжения
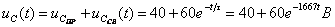 . (1.18)
. (1.18)
Токи найдём по формулам:
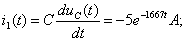
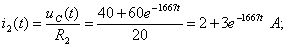 (1.19)
(1.19)
Построение графиков напряжения и токов среде Mathcad (см. рисунок 1.12, 1.13).
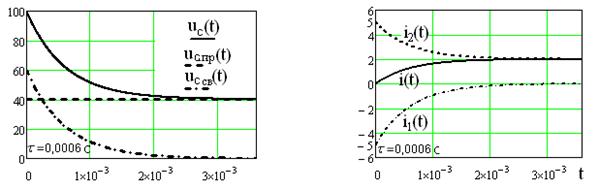
Рисунок 1.12 Рисунок 1.13
Цепи в виде резисторно-конденсаторного делителя нашли широкое применение в импульсных устройствах РЭТ.
1.2.3 Расчёт переходных процессов в цепях второго порядка.
Задача 1.5 Параллельный колебательный контур (см. рисунок 1.14) подключается к источнику ЭДС Е= 125В. Определить закон изменения напряжения 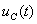 для трех случаев: 1.R= 250 Ом, L= 667 мГн, С = 2 мкФ;
для трех случаев: 1.R= 250 Ом, L= 667 мГн, С = 2 мкФ;
2. R = 100 Ом, L = 40мГн, С= 1 мкФ; 3. R = 100 Ом, L = 40мГн, С = 5мкФ.
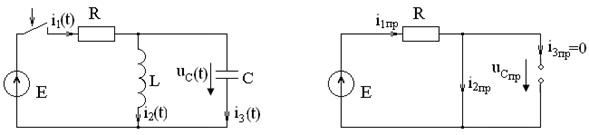 Рисунок 1.14 Рисунок 1.15
Рисунок 1.14 Рисунок 1.15
Решение: Записывают независимые начальные условия 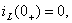
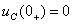 . Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации:
. Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации:
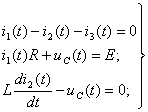 (1.20)
(1.20)
Переходное напряжение 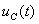 представляют в виде суммы принуждённой и свободной составляющих:
представляют в виде суммы принуждённой и свободной составляющих: 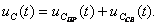
Определяют принуждённую составляющую напряжения на ёмкости. Так как в установившемся режиме цепи после коммутации (при 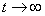 ) конденсатор шунтирован катушкой индуктивности накоротко (см. рисунок 1.15), принуждённая составляющую равна нулю:
) конденсатор шунтирован катушкой индуктивности накоротко (см. рисунок 1.15), принуждённая составляющую равна нулю: 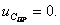
Вычисляют свободную составляющую напряжения на ёмкости. Для этого составляют характеристическое уравнение, например, методом входного сопротивления и определяют его корни:
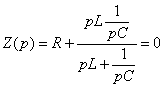 или (после преобразований)
или (после преобразований) 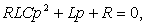
откуда 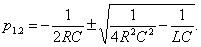 (1.21.)
(1.21.)
Вид свободной составляющей напряжения зависит от типа корней характеристического уравнения. Для трех заданных значений параметров рассчитывают корни р1,2.
1) R= 250 Ом, L= 667 мГн, С = 2 мкФ.
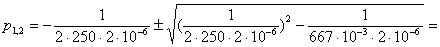
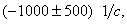
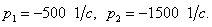
Корни действительные и различные. Свободная составляющая напряжения на конденсаторе имеет вид: 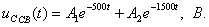
2) R = 100 Ом, L = 40мГн, С= 1 мкФ 
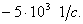
Корни действительные и равные 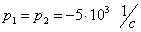 , следовательно,
, следовательно,
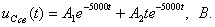
3) R = 100 Ом, L = 40мГн, С = 5мкФ

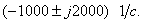
Корни комплексные сопряженные. Свободная составляющая напряжения на конденсаторе имеет вид: 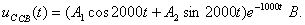
|
|
|
Постоянные интегрирования 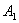 и
и 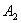 определяют из начальных условий
определяют из начальных условий
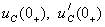 . Из выражения
. Из выражения 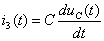 следует, что
следует, что 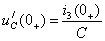 , и задача сводится к определению
, и задача сводится к определению 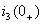 .Зависимое начальное условие
.Зависимое начальное условие 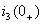 определяют из уравнений составленных по законам Кирхгофа (1.20), записанных для момента времени
определяют из уравнений составленных по законам Кирхгофа (1.20), записанных для момента времени 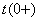 :
:
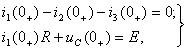
и с учётом независимых начальных условий 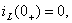
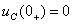 , получим:
, получим:
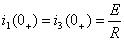 (1.22)
(1.22)
Найдём uc(t)для трех случаев корней:
1) R= 250 Ом, L= 667 мГн, С = 2 мкФ. Корни действительные и различные: 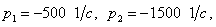 тогда:
тогда:
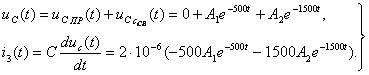
При 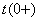 :
: 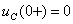 ,
, 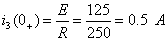 , получим
, получим
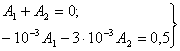
отсюда А1=250, А2=-250, и напряжение на ёмкости равно:
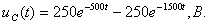
Графики напряжения uc(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16, а).
2) R = 100 Ом, L = 40мГн, С= 1 мкФ. Корни действительные и равные: 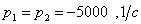 , тогда
, тогда
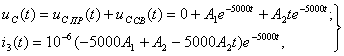
при 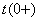 :
: 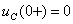 ,
, 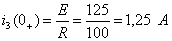 , получим
, получим 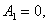
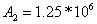 , и напряжение на ёмкости равно:
, и напряжение на ёмкости равно: 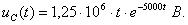
Графики напряжения uc(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,б).
3) R = 100 Ом, L = 40мГн, С = 5мкФ. Корни комплексные сопряженные
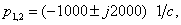 тогда
тогда
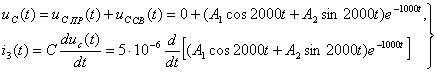
при 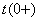 :
: 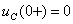 ,
, 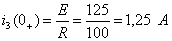 , получим
, получим 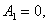
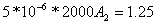 , отсюда
, отсюда 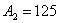 и напряжение на ёмкости будет равно:
и напряжение на ёмкости будет равно: 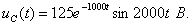
Графики напряжения uc(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,в).
Выводы
1 Напряжение uc(t ) при колебательном режиме представляет собой затухающее колебание.
2 Переходной процесс в параллельном колебательном контуре при при колебательном режиме используют в автоколебательных системах, где контур является нагрузочной цепью.
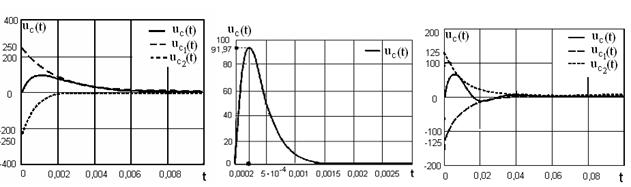
а) б) в)
Рисунок 1.16
Задача 1.6 Электрическая цепь (см. рисунок 1.17), в которой действует источник постоянной ЭДС 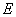 =
= 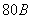 , находится в установившимся режиме. Параметры цепи:
, находится в установившимся режиме. Параметры цепи: 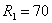 Ом,
Ом, 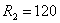 Ом,
Ом, 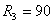 Ом,
Ом, 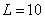 мГн, С=0,7 мкФ. В момент времени t=0 путем замыкания ключа К в цепи осуществляется коммутация. Определить ток
мГн, С=0,7 мкФ. В момент времени t=0 путем замыкания ключа К в цепи осуществляется коммутация. Определить ток 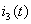 после замыкания ключа.
после замыкания ключа.
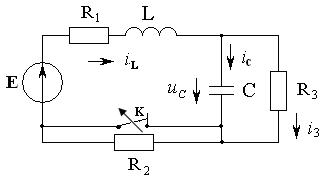
Рисунок 1.17
Решение: 1) Определение независимые начальные условия (ННУ). ННУ 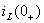 и
и 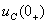 определяются путём расчета установившегося режима в цепи до коммутации. Установившийся режим до коммутации создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко замкнутым участком, а ёмкость размыкается (см. рисунок 1.18).
определяются путём расчета установившегося режима в цепи до коммутации. Установившийся режим до коммутации создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко замкнутым участком, а ёмкость размыкается (см. рисунок 1.18).
Ток в индуктивности и напряжение на ёмкости до коммутации найдём по формулам:
|
|
|
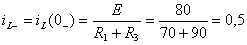 А;
А; 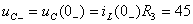 В.
В.
Независимые начальные условия определим по законам коммутации:
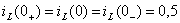 А,
А, 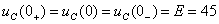 В.
В.
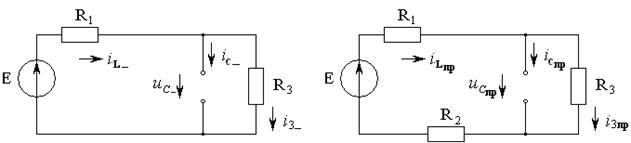
Рисунок 1.18 Рисунок 1.19
2) Составляется систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации, при t ≥0:
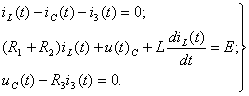 (1.23)
(1.23)
Переходный ток 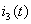 удовлетворяет системе уравнений (1.23) и может быть представлен в виде суммы токов принужденного и свободного режимов цепи:
удовлетворяет системе уравнений (1.23) и может быть представлен в виде суммы токов принужденного и свободного режимов цепи:
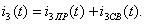 (1.24)
(1.24)
3) Определение тока в принужденном режиме. Принужденный ток 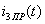 определяется путем расчета установившегося режима в цепи после коммутации. Установившийся режим после коммутации создается постоянной ЭДС, поэтому на схеме индуктивность заменяется короткозамкнутым участком, а ёмкость размыкается (см. рисунок 1.19). Принужденный ток
определяется путем расчета установившегося режима в цепи после коммутации. Установившийся режим после коммутации создается постоянной ЭДС, поэтому на схеме индуктивность заменяется короткозамкнутым участком, а ёмкость размыкается (см. рисунок 1.19). Принужденный ток 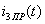 определяется по закону Ома:
определяется по закону Ома:
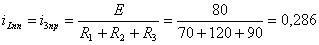 А; (1.25)
А; (1.25)
4) Определение свободного тока 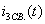 . Для определения свободного тока
. Для определения свободного тока 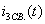 необходимо составить характеристическое уравнение цепи после коммутации. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления. Комплексное входное сопротивление для цепи после коммутации относительно ветви с источником ЭДС имеет вид:
необходимо составить характеристическое уравнение цепи после коммутации. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления. Комплексное входное сопротивление для цепи после коммутации относительно ветви с источником ЭДС имеет вид:
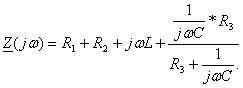 , (1.26)
, (1.26)
В формуле 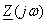
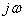 заменяется на р и полученное сопротивление
заменяется на р и полученное сопротивление 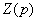 приравнивается к нулю:
приравнивается к нулю: 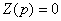 :
:
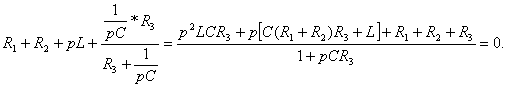
Приравняем к нулю числитель выражения 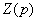 и получим характеристическое уравнение:
и получим характеристическое уравнение:
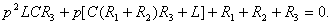 (1.27)
(1.27)
Подставим числовые значения:
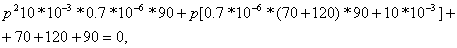
отсюда
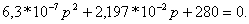 (1.28)
(1.28)
Корни характеристического уравнения (1.28):
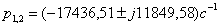 .
.
Так как корни характеристического уравнения комплексно-сопряженные, свободный ток 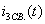 записывается в виде:
записывается в виде:
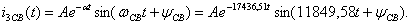 (1.29)
(1.29)
5) Определение постоянных интегрирования 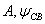 . Постоянные интегрирования определяются по начальным значениям тока
. Постоянные интегрирования определяются по начальным значениям тока 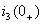 и его первой производной
и его первой производной 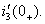 Записывается переходный ток:
Записывается переходный ток:
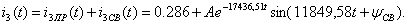
находится производная тока 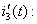


Записывается переходный ток 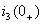 и производная тока
и производная тока 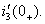 для момента времени
для момента времени 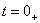 . Система уравнений для определения постоянных интегрирования имеет вид:
. Система уравнений для определения постоянных интегрирования имеет вид:
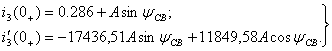 ; (1.30)
; (1.30)
Чтобы решить систему уравнений (1.30) и определить постоянные интегрирования 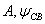 , нужно найти начальные значения (зависимые начальные условия)
, нужно найти начальные значения (зависимые начальные условия) 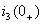 и
и 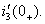 Зависимые начальные условия
Зависимые начальные условия 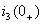 и
и 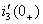 определяются по независимым начальным условиям
определяются по независимым начальным условиям 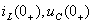 путем решения системы дифференциальных уравнений (1.23), составленных по законам Кирхгофа для цепи после коммутации и рассматриваемых для момента времени t=0+. Выразим ток
путем решения системы дифференциальных уравнений (1.23), составленных по законам Кирхгофа для цепи после коммутации и рассматриваемых для момента времени t=0+. Выразим ток 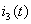 через независимые переменные
через независимые переменные 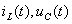 . Из третьего уравнения системы (1.23) определим ток
. Из третьего уравнения системы (1.23) определим ток 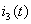 и найдём производную
и найдём производную 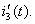 :
: 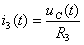 ;
; 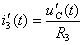 .
.
Так как ток в ёмкости равен 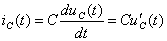 , производную
, производную 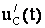 определим по формуле:
определим по формуле: 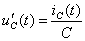 . Ток
. Ток 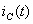 найдём из первого закона Кирхгофа:
найдём из первого закона Кирхгофа: 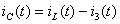 . Вычислим
. Вычислим 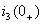 и
и 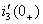 для момента времени
для момента времени 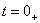 :
:
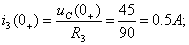
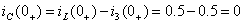 ;
;
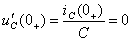 , отсюда
, отсюда 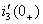 =0.
=0.
Подставим 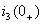 и
и 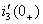 в систему (1.30) и определим постоянные интегрирования А и
в систему (1.30) и определим постоянные интегрирования А и 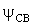 :
:
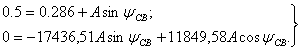 (1.31)
(1.31)
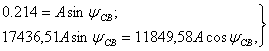 (1.32)
(1.32)
отсюда
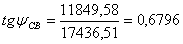
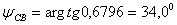
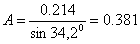
Подставим найденные значения А и 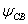 в выражения для тока
в выражения для тока 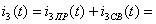
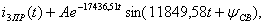 и окончательно получим:
и окончательно получим:
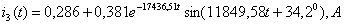 .
.
График тока 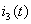 (см.рисунок 1.20) построен в среде Mathcad, в интервале времени
(см.рисунок 1.20) построен в среде Mathcad, в интервале времени
от 0 до 5τ, где 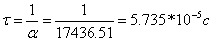 .
.
Чтобы наглядно показать, как 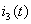 →
→ 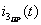 , и
, и 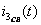 → 0, построены отдельно графики
→ 0, построены отдельно графики 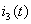 и
и 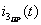 (рис.1 21) и
(рис.1 21) и 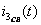 (рис.1.22) в интервале от 3τ до 8τ.
(рис.1.22) в интервале от 3τ до 8τ.
Рисунок 1.20 Рисунок 1.21 Рисунок 1.22
Задача 1.7 Электрическая цепь (см. рисунок 1.23), в которой действует источник синусоидальной ЭДС 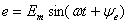 =
= 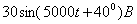 , находится в установившимся режиме. Параметры цепи:
, находится в установившимся режиме. Параметры цепи: 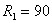 Ом,
Ом, 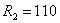 Ом,
Ом, 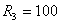 Ом,
Ом, 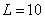 мГн, С=0,5мкФ. В момент времени t=0 путем замыкания ключа К в цепи осуществляется коммутация. Определить ток
мГн, С=0,5мкФ. В момент времени t=0 путем замыкания ключа К в цепи осуществляется коммутация. Определить ток 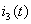 после замыкания ключа.
после замыкания ключа.
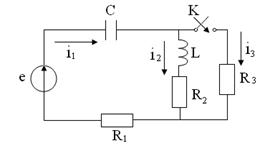
Рисунок 1.23
Решение: 1) Определение независимых начальных условий (ННУ): 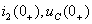 . ННУ определим путём расчета установившегося режима в цепи до коммутации. Установившийся режим до коммутации создается синусоидальной ЭДС. Для расчета установившегося режима применим комплексный метод. Эквивалентная схема цепи до коммутации для расчета комплексным методом показана на рисунке 1.24.
. ННУ определим путём расчета установившегося режима в цепи до коммутации. Установившийся режим до коммутации создается синусоидальной ЭДС. Для расчета установившегося режима применим комплексный метод. Эквивалентная схема цепи до коммутации для расчета комплексным методом показана на рисунке 1.24.
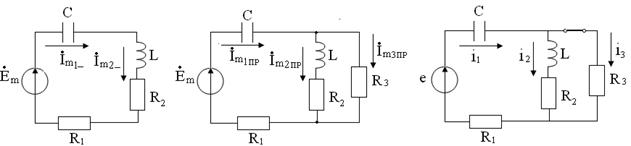
Рисунок 1.24 Рисунок 1.25 Рисунок 1.26
Комплексная амплитуда ЭДС: 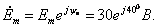 Индуктивное и емкостное сопротивления:
Индуктивное и емкостное сопротивления: 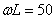 Ом,
Ом, 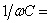 Ом. Комплексное сопротивление цепи, комплексная амплитуда тока и комплексная амплитуда напряжения на ёмкости равны:
Ом. Комплексное сопротивление цепи, комплексная амплитуда тока и комплексная амплитуда напряжения на ёмкости равны:
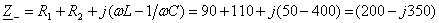 Ом,
Ом,
 А,
А,
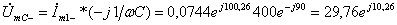 В.
В.
Запишем мгновенные значения тока в индуктивности 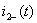 и напряжения на емкости
и напряжения на емкости 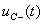 :
:
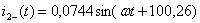 А,
А, 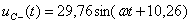 В. (1.33)
В. (1.33)
Определим мгновенные значения тока в индуктивности 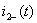 и напряжения на емкости
и напряжения на емкости 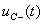 в момент времени t=0−:
в момент времени t=0−:
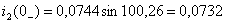 А,
А, 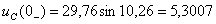 В.
В.
Независимые начальные условия найдем по законам коммутации:
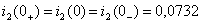 А,
А, 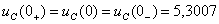 В. (1.34)
В. (1.34)
2) Составление системы дифференциальных уравнений. Дифференциальные уравнения составляются по законам Кирхгофа для цепи после коммутации (см. рисунок 1.26) для t ≥0 и имеют вид:
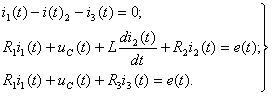 (1.35)
(1.35)
Переходный ток 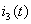 удовлетворяет системе уравнений (1.35) и может быть представлен в виде суммы токов принужденного и свободного режимов цепи:
удовлетворяет системе уравнений (1.35) и может быть представлен в виде суммы токов принужденного и свободного режимов цепи:
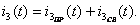 (1.36)
(1.36)
3) Определение тока 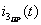 в принужденном режиме.
в принужденном режиме.
Принужденный ток 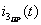 определяется путем расчета установившегося режима в цепи после коммутации. Установившийся режим после коммутации создается синусоидальной ЭДС. Для расчета установившегося режима применим комплексный метод (см. рисунок 1.25). Комплексная амплитуда ЭДС:
определяется путем расчета установившегося режима в цепи после коммутации. Установившийся режим после коммутации создается синусоидальной ЭДС. Для расчета установившегося режима применим комплексный метод (см. рисунок 1.25). Комплексная амплитуда ЭДС: 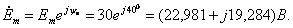 Комплексное сопротивление цепи:
Комплексное сопротивление цепи:
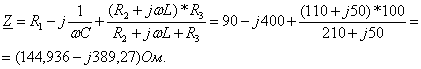
Найдём комплексные амплитуды принужденных токов 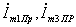 , используя закон Ома и формулу разброса:
, используя закон Ома и формулу разброса:
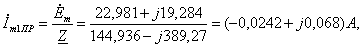
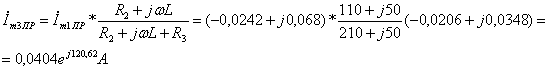
Мгновенное значение принужденного тока 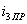 равно:
равно:
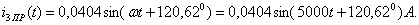 (1.37)
(1.37)
4) Определение свободного тока 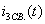 .
.
Для определения свободного тока 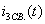 составляют характеристическое уравнение цепи после коммутации. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления.
составляют характеристическое уравнение цепи после коммутации. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления.
Запишем комплексное входное сопротивление для цепи после коммутации относительно ветви с источником ЭДС:
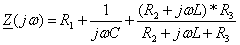 .
.
В формуле 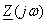 заменяют
заменяют 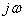 на р и полученное сопротивление
на р и полученное сопротивление 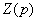 приравнивают к нулю:
приравнивают к нулю: 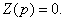
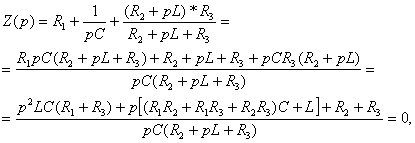 (1.38)
(1.38)
Приравнивают к нулю числитель 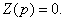 и получают характеристическое уравнение:
и получают характеристическое уравнение:
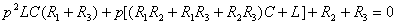 . (1.39)
. (1.39)
После подстановки числовых значений:
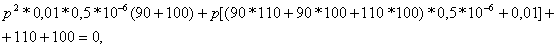
получают: 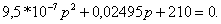 (1.40)
(1.40)
Определяют корни характеристического уравнения (1.40):
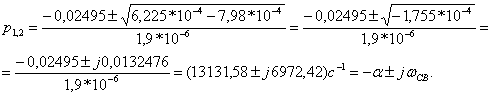
Корни характеристического уравнения комплексно-сопряженные, свободный ток 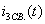 представляют в виде:
представляют в виде:
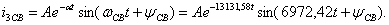 (1.41)
(1.41)
Переходный ток равен:
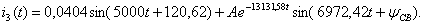 (1.42)
(1.42)
5) Определение постоянных интегрирования 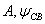 .
.
Постоянные интегрирования определяются по начальным значениям тока 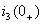 и его первой производной
и его первой производной 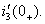 Запишем переходный ток
Запишем переходный ток 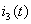 и найдем производную тока
и найдем производную тока 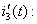
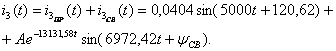
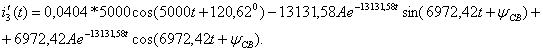
Записываются начальные значения тока 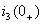 и его первой производной
и его первой производной 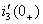 , в момент времени t=0+ и получают систему уравнений для определения постоянных интегрирования
, в момент времени t=0+ и получают систему уравнений для определения постоянных интегрирования 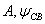 :
:
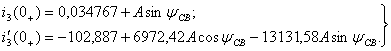 (1.43)
(1.43)
Чтобы решить систему уравнений (1.43) и определить постоянные интегрирования 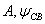 , нужно найти
, нужно найти 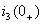 и
и 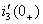 ,которые определяются по независимым начальным условиям
,которые определяются по независимым начальным условиям 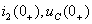 путем решения системы дифференциальных уравнений (1.35), рассматриваемых для момента времениt=0+. Выражают ток
путем решения системы дифференциальных уравнений (1.35), рассматриваемых для момента времениt=0+. Выражают ток 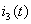 через независимые переменные
через независимые переменные 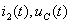 , из первого закона Кирхгофа имеем:
, из первого закона Кирхгофа имеем: 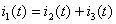 , подставляют полученное выражение для тока
, подставляют полученное выражение для тока 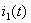 в третье уравнение системы (1.35):
в третье уравнение системы (1.35):
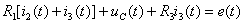 , и найдем
, и найдем 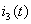 и
и 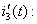
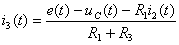 ;
; 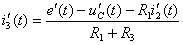
где 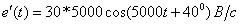 .
.
Для момента времени t=0+ рассчитывают 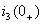 :
:
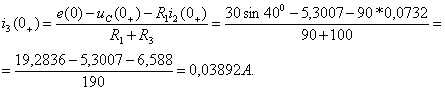
Чтобы определить 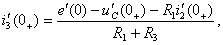 вычисляют
вычисляют
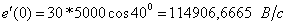 ;
; 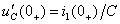 и
и 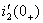
находят из системы дифференциальных уравнений (1.35), рассматриваемых для момента времени t=0+:
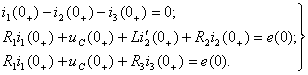 (1.44)
(1.44)
Ток 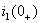 определяют из первого уравнения системы (1.44):
определяют из первого уравнения системы (1.44):
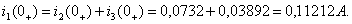
По найденному значению тока 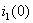 , вычисляют:
, вычисляют:
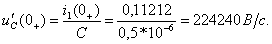
Производную тока 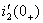 определяют из второго уравнения системы (1.44):
определяют из второго уравнения системы (1.44):
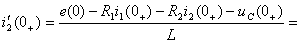
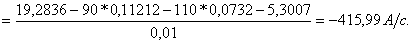
По найденным значениям 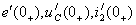 определяют
определяют 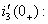
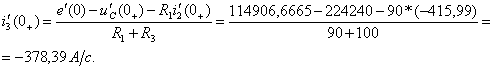
Подставляют найденные значения 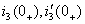 в систему уравнений (1.43) и определяют постоянные интегрирования
в систему уравнений (1.43) и определяют постоянные интегрирования 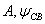 .
.
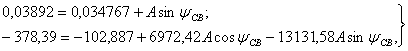 (1.45)
(1.45)
отсюда:
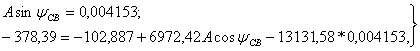 (1.46)
(1.46)
или
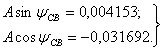 (1.47)
(1.47)
Делят первое уравнение системы (1.47) на второе определяют постоянные интегрирования:
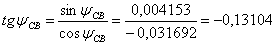 ,
, 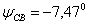 и
и
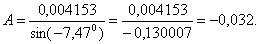
Подставляют найденные значения 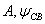 в выражение (1.42) и получают переходный ток
в выражение (1.42) и получают переходный ток 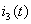 :
:
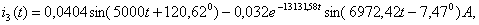
где 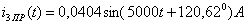 - принуждённый ток,
- принуждённый ток,
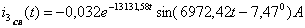 - свободный ток.
- свободный ток.
График тока 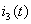 (см. рисунок 1.27) построен в среде Mathcad, в интервале времени
(см. рисунок 1.27) построен в среде Mathcad, в интервале времени
от 0 до 6τ, где 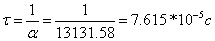 .
.

Рисунок 1.27
 2015-04-01
2015-04-01 3033
3033
