Случайная величина

Случайная величина как фундаментальное понятие теории вероятности имеет большое значение в ее приложениях. Это понятие является абстрактным выражением случайного события. Более того, оперировать со случайными величинами иногда более удобно, чем со случайными событиями.

Случайной называется величина, которая в результате опыта может принять то или иное (но только одно) значение (до опыта неизвестно, какое именно).

События принято обозначать большими буквами латинского алфавита, вероятность буквой Р, например, Р(А). Реализации события (случайные величины) обозначаются малыми буквами: a ₁, a ₂, …, a _n.

Поскольку в теории вероятностей и математической статистике рассматриваются массовые явления, то случайная величина, как правило, характеризуется возможными значениями и их вероятностями.

Среди встречающихся в практике случайных величин можно выделить дискретные и непрерывные.

Дискретными случайными величинами называются такие, которые принимают только отделенные друг от друга значения и могут быть заранее перечислены. Например, количество автомобилей на заданном километровом участке дороги в конкретный момент времени; число бракованных узлов деталей автомобиля в партии из n штук.

Для дискретных случайных величин характерно, что они принимают отдельные, изолированные значения, которые можно заранее перечислить. Например, количество автомобилей на заданном участке дороги может принимать только целочисленные значения 0, 1,2,..., п и зависит от времени суток и интенсивности движения.

Существуют случайные величины другого типа, которые чаще встречаются и имеют большое практическое значение.

Непрерывной случайной величиной называется такая, возможные значения которой непрерывно заполняют некоторый промежуток (интервал числовой оси). Интервал числовой оси может быть конечным или бесконечным. Примерами непрерывных случайных величин являются время безотказной работы автомобиля в заданных дорожных условиях, скорость движения автомобиля на заданной дороге, ошибка измерения.

В отличие от дискретных возможные значения непрерывных случайных величин нельзя заранее перечислить, так как они непрерывно заполняют некоторый промежуток.

Случайные величины обозначаются обычно большими буквами латинского алфавита - X, Y, Z, Т, а их возможные значения соответствующими малыми x_i, y_i, z_i, t_i, где i = 1, 2,.... п.

Рассмотрим дискретную случайную величину X с возможными значениями x ₁, x ₂, …, x_n. В результате проведения многократных опытов величина Т может принять каждое из значений x_i, т. е.:

X = x₁; X = x₂; …; X = x_n.

Обозначим вероятности этих событий буквой р с соответствующими индексами:

P(X = x₁)= p₁; P(X = x₂)= p₂; …; P(X = x_n)= p_n.

Последнюю формулу следует читать так: вероятность того, что случайная величина Т примет конкретное значение x ₁, равна p ₁ и т.д.

Исходя из того, что события x_i образуют полную группу несовместимых событий, т. е. никаких других событий произойти не может, сумма вероятностей всех возможных значений случайной величины Т равна единице.

Эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины

Дискретную случайную величину можно полностью описать с вероятностной точки зрения, если точно указать вероятность каждого события, т. е. задать это распределение. Этим будет установлен закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Зная его, можно до опыта судить о том, какие значения случайной величины будут появляться чаще и какие реже. Способы или формы представления закона распределения случайной величины различны.

Простейшей формой задания закона распределения дискретной случайной величины Т является ряд распределения или таблица, в которой перечислены возможные значения этой величины и соответствующие им вероятности:

xi	x 1	x 2	…	xn
pi	p 1	p	…	pn

Чтобы придать ряду распределения дискретных случайных величин более наглядный вид, его часто изображают графически.

При графическом представлении все возможные значения случайной величины откладывают по оси абсцисс, а соответствующие вероятности - по оси ординат.

Вершины полученных ординат обычно соединяют прямыми или пунктирными линиями. Это особенно целесообразно, если на одном графике представлено несколько кривых распределений. Соединяют вершины только для наглядности, так как в промежутках между соседними значениями случайная величина X значений принять не может, так как она дискретная, а ее вероятность в этих промежутках равна нулю. Такая фигура, изображенная на рис. 2.1, называется многоугольником распределения.

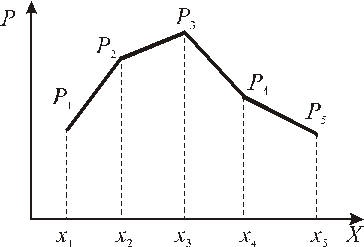Рис. 2.1. Многоугольник распределения дискретной случайной величины

Многоугольники распределения могут принимать различные формы. Однако все они обладают общим свойством: сумма ординат многоугольника распределения, представляющая сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Следует особо разграничить деление случайных величин на дискретные и непрерывные. Так, ряд распределения является удобной формой представления закона распределения для дискретной случайной величины, характеризуемой конечным числом возможных значений. Однако для непрерывной случайной величины ряд распределения вообще нельзя построить, поскольку она характеризуется бесчисленным множеством возможных значений, которые сплошь заполняют некоторый промежуток, и перечислить их в таблице трудно.

Различные диапазоны возможных значений случайной величины все же являются неодинаково вероятными, и для непрерывной величины существует распределение величин интервалов, а не конкретных значений.

Для количественной оценки этого распределения вероятностей используется не вероятность события X = x, а вероятность события X < x (x - некоторая текущая величина).

Вероятность этого события зависит от x является функцией от x, которая называется функцией распределения случайной величины Т и обозначается F(x).

Функцию распределения F(x) иногда называют интегральной функцией, или интегральным законом, распределения. Она существует для дискретных и непрерывных случайных величин и является самой универсальной их характеристикой

График функции F(x) представляет неубывающую функцию, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрыв).

Обычно для дискретной случайной величины функция распределения F(x) всегда разрывная ступенчатая, скачки которой происходят в точках, соответствующих возможным значениям и равны вероятностям этих значений. Для непрерывной случайной величины она непрерывна во всех точках.

Графическое представление функции распределения удобно для решения практических задач, связанных с определением вероятности того, что случайная величина примет значение, заключенное в некоторых пределах от x ₁ до x ₂. Это событие равносильно попаданию величины X на участок от x ₁ до x ₂ и равно приращению функции распределения на этом участке

Р (x ₁ £ X £ x ₁) = F (x ₁) – F (x ₂).