Определение основных понятий теории полумарковских процессов

Глава 6. Полумарковские процессы

Обобщением цепей Маркова с непрерывным временем являются полумарковские случайные процессы с дискретным множеством состояний, реализации которых, аналогично цепям Маркова, являются кусочно постоянными непрерывными справа функциями.

В это главе будет дано определение полумарковского процесса, процесса марковского восстановления, полумарковской матрицы, определяющей такие процессы, вложенной цепи Маркова для полумарковского процесса, а также будут определены другие понятия, необходимые для рассмотрения полумарковских процессов. Достаточно детально будет рассмотрен метод дополнительных переменных для анализа процессов марковского восстановления и полумарковских процессов

Определение основных понятий теории полумарковских процессов

Рассмотрим однородный двумерный марковский случайный процесс {x(n),t(n)} с дискретным временем n =0,1,2,…, первая компонента x(n) которого принимает значения из некоторого дискретного множества. Для определённости будем полагать, что x(n)=1,2,…. Вторая компонента t(n) принимает неотрицательные значения (вообще говоря, из непрерывного множества).

По определению, марковской переходной функцией F (k ₂, x; k ₁, y) однородного двумерного марковского случайного процесса{x(n),t(n)} называется

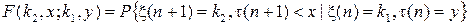. (1)

Будем рассматривать только такие двумерные случайные процессы {x(n),t(n)}, для марковских переходных функций которых выполняются равенства

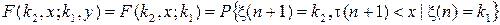, (2)

то есть условное распределение (1) не зависит от второго условия t(n)= y (не зависит от значения второй компоненты t(n) рассматриваемого двумерного марковского процесса).

В этом случае марковскую переходную функцию F (k ₂, x; k ₁) будем обозначать

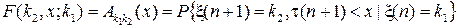. (3)

Матрицу A (x), элементами которой являются функции A_{k n}(x), определяемые равенством (3), будем называть полумарковской.

Определим последовательность моментов времени

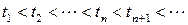
равенством

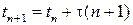
и некоторым начальным условием на t ₀.

Теперь можно дать следующее определение.

Случайный процесс k (t) с дискретным множеством состояний и непрерывным временем t будем называть полумарковским, заданным полумарковской матрицей A (x), если для всех n выполняются равенства

.

То есть, на каждом интервале времени [ t_n, t_{n +1}), длительность которого совпадает со значением второй компоненты t(n+ 1), процесс k (t) принимает и сохраняет то значение, которое в начале этого интервала приняла первая компонента x(n), рассматриваемого двумерного марковского процесса {x(n),t(n)}.

В силу свойства (2), первая компонента x(n) рассматриваемого марковского процесса также является марковским процессом, точнее цепью Маркова с дискретным временем и матрицей P вероятностей P_{k n} переходов за один шаг, определяемой равенством

.

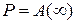Эта цепь x(n) для рассматриваемого полумарковского процесса k (t) называется вложенной цепью Маркова.

Вторая компонента {t(n)} процесса {x(n),t(n)} является немарковским процессом (последовательностью зависимых случайных величин), но для её элементов t(n) можно в силу равенства (3) определить условную функцию распределения

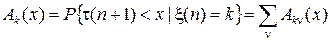. (4)

В стационарном режиме функционирования полумарковского процесса по формуле полной вероятности можно записать и безусловную функцию распределения F (x) времени пребывания процесса k (t) в каждом состоянии

,

где r (k) – стационарное распределение вероятностей значений вложенной цепи Маркова x(n).

Как известно, стационарное распределение вероятностей r (k) является решением системы линейных алгебраических уравнений

.

Если компоненты x(n) и t(n) двумерного случайного процесса {x(n),t(n)} условно независимы, то есть для элементов A_{k n}(x) полумарковской матрицы A (x) выполняются равенства

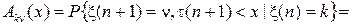
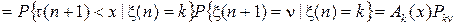, (5)

то полумарковский процесс k (t) будем называть процессом марковского восстановления.

Это название оправдано тем, что в классической теории восстановления рассматриваются самовосстанавливающиеся устройства в виде элемента с конечным сроком службы. Как только этот элемент отказывает, выходит из строя, он заменяется новым элементом того же вида, который рано или поздно заменяется третьим элементом, и так далее.

Пусть имеются элементы разных видов, которыми можно заменять отказавшие элементы. Срок службы элемента вида k является случайной величиной с функцией распределения A_k (x). Будем полагать, что заданы вероятности P_{k n} того, что если выходит из строя элемент вида k, то его заменяют элементом вида n.

Процесс k (t), определяющий вид элемента работающего в момент времени t, является процессом марковского восстановления.

В силу равенства (5) для процессов марковского восстановления полумарковскую матрицу A (x) можно записать в виде произведения

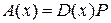, (6)

где D (x) – диагональная матрица с элементами A_k (x) по главной диагонали.

В силу определения (3) элементы A_{k n}(x) полумарковской матрицы определяют условные двумерные распределения вероятностей, задание которых вызывает некоторые затруднения, поэтому достаточно полезной является следующая мультипликативная форма этих элементов

,

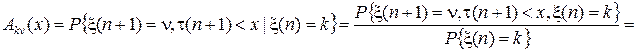
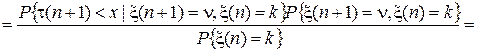
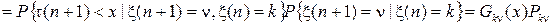то есть A_{k n}(x) можно записать в виде произведения

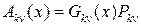, (7)

где G_{k n}(x) – условная функция распределения времени пребывания полумарковского процесса в k -ом состоянии при условии, что переход будет осуществлён в состояние n.

Из (7) следует, что полумарковскую матрицу A (x) можно записать в виде произведения Адамара

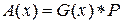
матриц G (x) и P с элементами

,

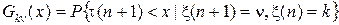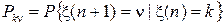. (8)

Задание полумарковского процесса матрицами G (x) и P гораздо проще, чем полумарковской матрицей A (x), но задание полумарковской матрицей более компактно.