Достаточные условия экстремума функции.
Определение. Пусть функция f (x) определена всюду в некоторой окрестности точки с. Говорят, что функция f (x) имеет в точке с локальный максимум (минимум), если существует такая окрестность точки с, в пределах которой значение f (с) является наибольшим (наименьшим).
Локальный максимум и минимум объединяются общим названием экстремум.
Первое достаточное условие экстремума.
Теорема 9.1. Пусть
- точка с является точкой возможного экстремума функции f (x),
- f (x) дифференцируема всюду в некоторой окрестности точки с.
Тогда, если в пределах указанной окрестности 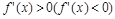 слева от точки с и
слева от точки с и 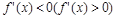 справа от точки с, то функция f (x) имеет в точке с локальный максимум (минимум). Если же f’ (x) имеет один и тот же знак слева и справа от точки с, то экстремума в точке с нет.
справа от точки с, то функция f (x) имеет в точке с локальный максимум (минимум). Если же f’ (x) имеет один и тот же знак слева и справа от точки с, то экстремума в точке с нет.
Доказательство.
1). Пусть 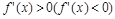 слева от точки с и
слева от точки с и 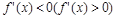 справа от с. Обозначим x 0 ¹ c любое значение аргумента из рассматриваемой окрестности. Достаточно доказать, что
справа от с. Обозначим x 0 ¹ c любое значение аргумента из рассматриваемой окрестности. Достаточно доказать, что
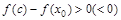
Функция f (x) дифференцируема (а следовательно, непрерывна) на сегменте 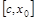 . По формуле Лагранжа (формула конечных приращений)
. По формуле Лагранжа (формула конечных приращений)
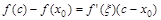 (1)
(1)
где x лежит между c и x 0. Т.к. 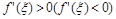 при
при 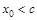 и
и 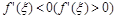 при
при 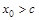 , то правая часть (1) положительна (отрицательна).
, то правая часть (1) положительна (отрицательна).
2). Пусть теперь f’ (x) имеет один и тот же знак слева и справа от c. Обозначая через x 0 любое значение аргумента, отличное от c, и повторяя проведенные выше рассуждения, мы докажем, что правая часть (1) имеет разные знаки слева и справа от с. Это доказывает отсутствие экстремума в точке с.
 2015-04-20
2015-04-20 3266
3266