Если каждому значению n из натурального ряда чисел 1,2,...,n,... ставится в соответствие по определенному закону некоторое вещественное число xn, то множество занумерованных вещественных чисел x1,x2,...,xn,... (1) мы и будем называть числовой последовательностью или просто последовательностью.
Определение. Последовательность {xn} называют ограниченной сверху (снизу), если существует вещественное число М (вещественное число m) такое, что каждой элемент этой последовательности xn удовлетворяет неравенству xn<М (xn>m).
При этом число М (число m) называют верхней гранью (нижней гранью) последовательности {xn}, а неравенство xn<М(xn>m) называют условным ограничением этой последовательности сверху (снизу).
Определение. Последовательность {xn} называется ограниченной с обеих сторон (или просто ограниченной), если она ограничена и сверху, и снизу, т.е. если существуют два вещественных числа M и m такие, что каждый элемент этой последовательности xn удовлетворяет неравенствам m<xn<М. (2)
При этом числа m и М называют соответственно нижней и верхней гранями последовательности {xn}, а неравенства (2) называют условно ограниченной последовательностью.
|
|
|
Последовательность {xn} является ограниченной тогда и только тогда, когда существует положительное вещественное число А такое, что каждый элемент последовательности xn удовлетворяет неравенству: ∣ xn∣≤ А. (3)
Последовательность {xn} называет неограниченной, если для любого положительного вещественного числа А* найдется хотя бы один элемент последовательности xn, удовлетворяющий неравенству ∣ xn∣> А*. (4)
4.Предел функции. Свойства пределов.
Предел функции в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Виды:
Предел функции по Гейне
Предел функции по Коши
Окрестностное определение по Коши
Предел по базе множеств
|
|
|
Свойства пределов числовых функций
Пусть даны функции 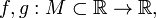 и
и 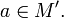 .
.
§ Одна и та же функция в одной и той же точке может иметь только один предел.
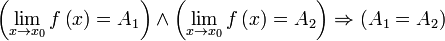
Доказательство [показать]
§ Сходящаяся функция локально сохраняет знак. Более обще,
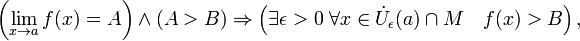
где 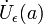 — проколотая окрестность точки a.
— проколотая окрестность точки a.
§ В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
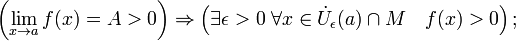
§ Сходящаяся функция локально ограничена в окрестности предельной точки:
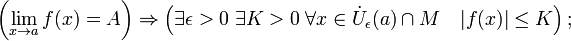
§ Отделимость от нуля функций, имеющих предел, отличный от нуля.
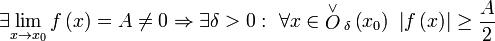
§ Операция взятия предела сохраняет нестрогие неравенства.
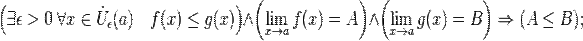
§ Правило двух милиционеров
§ Предел суммы равен сумме пределов:
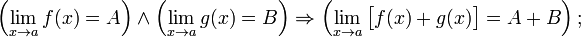
§ Предел разности равен разности пределов:
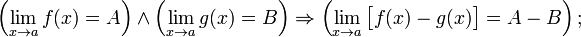
§ Предел произведения равен произведению пределов:
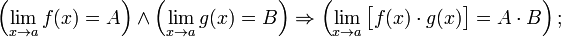
§ Предел частного равен частному пределов.
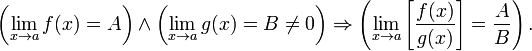
 2015-04-20
2015-04-20 2849
2849
