Пусть некоторое событие A может произойти при условии, что появится одно из несовместных событий (гипотез) B 1, B 2,..., Bn, образующих полную группу событий.
Вероятность события A, которое может наступить лишь при появлении одного из несовместных событий B 1, B 2,..., Bn, образующих полную группу событий, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
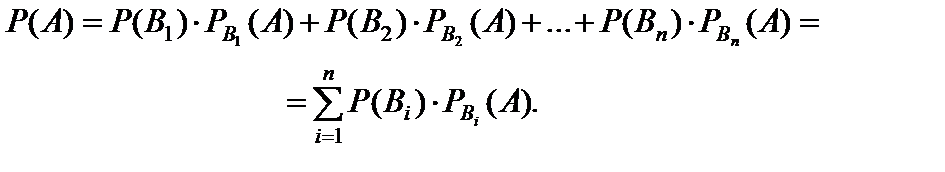 (26)
(26)
Это равенство называют формулой полной вероятности, где 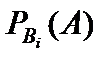 – вероятность наступления события A при наступлении гипотезы Bi.
– вероятность наступления события A при наступлении гипотезы Bi.
Пусть событие A произошло. Это изменит вероятности гипотез B 1, B 2,..., Bn и условная вероятность гипотезы PA (Bk) в предположении, что событие A произошло, определится по формуле Бейеса:
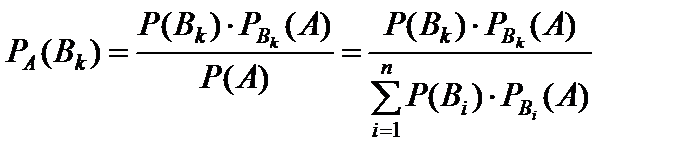 . (27)
. (27)
Пример 1.22. В урне 10 шаров, из них 4 белых. Один шар, цвет которого неизвестен, укатился. Из урны наугад вынимается один шар. Какова вероятность того, что он будет белым?
Решение. Пусть событие A – «вынутый шар белый». Возможны следующие предположения (гипотезы) о цвете укатившегося шара:
B 1 – «утерянный шар белый», B 2 – «утерянный шар не белый».
|
|
|
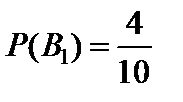 ;
; 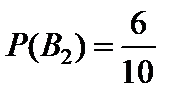 .
.
Вероятность вынуть белый шар при условии, что укатился белый шар, равна 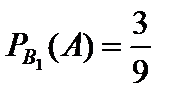 . Вероятность вынуть белый шар при условии, что укатился не белый, равна
. Вероятность вынуть белый шар при условии, что укатился не белый, равна 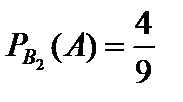 .
.
Согласно формуле полной вероятности (26) определим искомую вероятность:
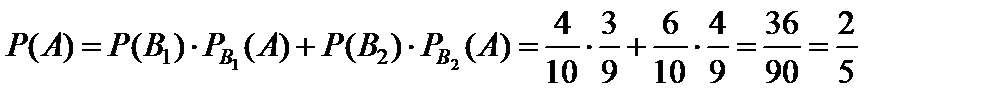 .
.
Пример 1.23. Имеются 3 одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором – три белые и одна серая, в третьем – две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?
Решение. Событие A – «из наугад выбранного ящика извлечена белая мышь». Возможны следующие гипотезы: B 1 – «выбор первого ящика», B 2 – «выбор второго ящика», B 3 – «выбор третьего ящика».
Так как все ящики одинаковы, то 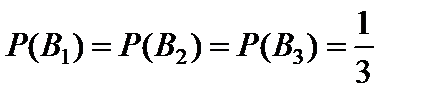 .
.
Вероятность выбора белой мыши из первого ящика равна 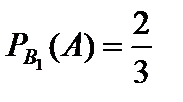 , вероятность выбора белой мыши из второго ящика –
, вероятность выбора белой мыши из второго ящика – 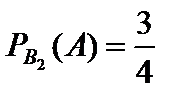 , вероятность выбора белой мыши из третьего ящика –
, вероятность выбора белой мыши из третьего ящика – 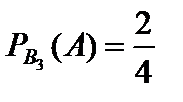 .
.
Следовательно, 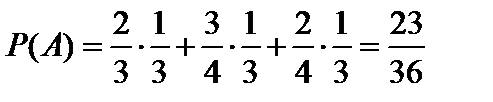 .
.
Пример 1.24. Три охотника произвели залп, причем две пули попали в лису. Какова вероятность того, что первый охотник попал в цель, если вероятности попадания первым, вторым и третьим охотниками соответственно равны 0,4; 0,3; 0,5?
Решение. По условию p 1 = 0,4, p 2 = 0,3, p 3 = 0,5. Тогда по формуле (18) q 1 = 1 – 0,4 = 0,6, q 2 = 1 – 0,3 = 0,7, q 2 = 1 – 0,5 = 0,5.
Пусть событие А – «два охотника попали в лису». Приведем два предположения (гипотезы): B 1 – «первый охотник попал в лису»,
B 2 – «первый охотник не попал в лису».
По условию P (B 1) = p 1 = 0,4; P (B 2) = q 1 = 0,6.
Искомая вероятность того, что первый охотник попал в лису, по формуле Бейеса (27) равна:
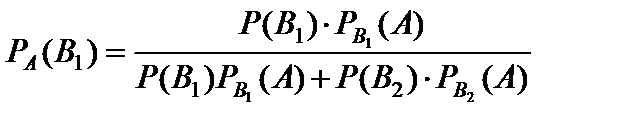 .
.
Найдем условную вероятность того, что в лису попали два охотника, причем одна пуля принадлежит первому охотнику. Следовательно, вторая пуля принадлежит либо второму, либо третьему охотнику:
|
|
|
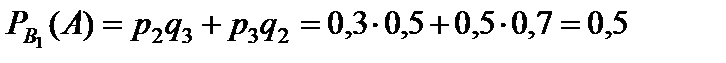 .
.
Вероятность того, что в лису попали два охотника, причем первый промахнулся, равна 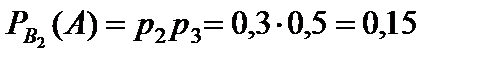 .
.
Следовательно, 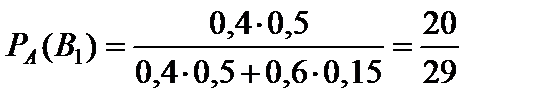 .
.
 2015-04-20
2015-04-20 2564
2564
