2015-04-30
482
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
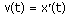
26.) Производная сложной функции. Производная обратных функций. Производные элементарных функции (вывод)
Пусть у = f(и) и u = φ(х) - тогда у = f(φ{x)) — сложная функция с промежуточным аргументом и н независимым аргументом х.
По условию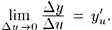 
Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем
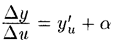или 
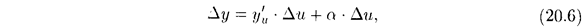где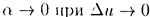 
.
Функция u = φ(х) имеет производную в точке х: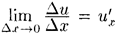 
, поэтому
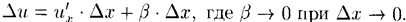Подставив значение Δ и в равенство (20.6), получим
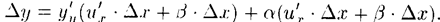т.е.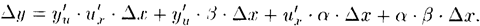 
Разделив полученное равенство на Δ х и перейдя к пределу при Δ х→ 0, получим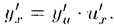 
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), u = φ(v), v = g{х), то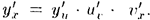 
Пусть у = f(x) и х = φ(y) — взаимно обратные функции.
Рассмотрим обратную функцию х = φ(y). Дадим аргументу у приращение Δ у ≠ 0. Ему соответствует приращение Δ х обратной функции, причем Δ х ≠ 0 в силу строгой монотонности функции у = f(x). Поэтому можно записать 
Если Δ y→ 0, то в силу непрерывности обратной функции приращение Δ х→ 0. И так как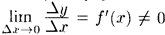 
, то из (20.7) следуют равенства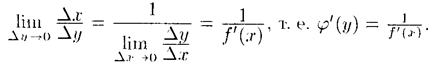 
|
|
|
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Правило дифференцирования обратной функции записывают так:
Пример 1. Найти производную функции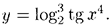 
Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: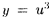 
, где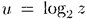 
, где z = tg q, где q =. 
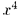. По правилу дифференцирования сложной функции (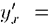
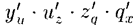)получаем:
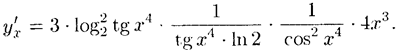Пример 2. Пользуясь правилом дифференцирования обратной функции, найти производную 
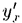для функции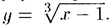 
Решение: Обратная функция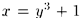 
имеет производную 
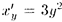. Следовательно,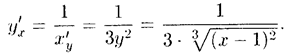 
Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.
Итак, производные элементарных функций:
| Название | Функция | Производная |
| Константа | f (x) = C, C ∈ R | 0 (да-да, ноль!) |
| Степень с рациональным показателем | f (x) = x n | n · x n − 1 |
| Синус | f (x) = sin x | cos x |
| Косинус | f (x) = cos x | − sin x (минус синус) |
| Тангенс | f (x) = tg x | 1/cos2 x |
| Котангенс | f (x) = ctg x | − 1/sin2 x |
| Натуральный логарифм | f (x) = ln x | 1/ x |
| Произвольный логарифм | f (x) = log a x | 1/(x · ln a) |
| Показательная функция | f (x) = e x | e x (ничего не изменилось) |
Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:
|
|
|
(C · f)’ = C · f ’.
В общем, константы можно выносить за знак производной. Например:
(2 x 3)’ = 2 · (x 3)’ = 2 · 3 x 2 = 6 x 2.
Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.
27.) Теорема Ролля. Теорема Ферма.27+ 28+
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)
Пусть функция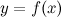 
1. непрерывна на отрезке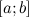 
;
2. дифференцируема на интервале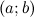 
;
3. на концах отрезка 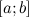принимает равные значения 
.
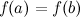Тогда на интервале 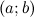найдется, по крайней мере, одна точка 
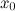, в которой 
.
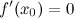Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
