Непрерывность функции нескольких переменных в точке и его свойства

Функция f(Pn) называется непрерывной в точке Po, если 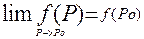. Непрерывна на мн-ве D, еслиона непрерывна в каждой т., этого мн-ва.

Св-ва:

1. сумма произведения и частное (если делитель ≠0) есть непрер. функции

2. f непрер. на огран. замкнутом мн-ве принимает на этом мн-ве своё наим. и наиб. знач-е

3. f непрер. на огран. замкнутом мн-ве и принимает на этом мн-ве любое знач-е, заключ. м/д m и M.

Дифференцируемость функции нескольких переменных. Необходимое условие дифференцируемости.

Пусть ф-ия z=f(x,y) определена на некот. δ-окрест. т. Mo(x0,y0) и пусть M(x,y) принадлежат этой окр.

Пусть ∆x=x-x0, ∆y=y-y0, тогда: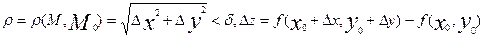

Ф-ия z=f(x,y) назыв. дифференц. в точке Mo(x0,y0), если сущ-ют два числа А и В, таких, что: ∆z=A∆x+B∆y+α(∆x, ∆y), где α(∆x, ∆y) –ε(∆x, ∆y)ρ, ρ≠0.

Необходимое условие дифф-ти, если fz=f(x,y) дифф-мы в т. Po(x0,y0), то в этой т. сущ-ют частные производные ф-ции, прчием f’x(Po)=A, f’y(Po)=B, где А и В – числа из