Необходимое условие идентификации (счётное правило)

Если обозначить число эндогенных переменных в j–м уравнении системы через H, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, – через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Если D + 1 = H, то уравнение скорее всего идентифицируемо,

если D + 1 < H, то уравнение неидентифицируемо,

если D + 1 > H, то уравнение сверхидентифицируемо.

Предположим, рассматривается следующая система одновременных уравнений:

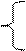y₁ = b₁₂∙y₂+b₁₃∙y₃+a₁₁∙x₁+a₁₂∙x₂,

y₂ = b₂₁∙y₁+a₂₁∙x1+a₂₂∙x2+a₂₃∙x₃,

y₃ = b₃₁∙y1+b₃₂∙y2+a₃₃∙x3+a₃₄∙x₄.

Первое уравнение скорее всего точно идентифицируемо, ибо в нем присутствуют три эндогенные переменные – y₁, y₂, y₃, т.е. H = 3 и две экзогенные переменные – x₁ и x₂, число отсутствующих экзогенных переменных равно двум – x₃ и x₄, D = 2. Тогда имеем равенство: D+1 = H, (так как 2+1 = 3), что означает, что это уравнение является подозрительным на то, что оно точно (просто) идентифицируемого уравнения. Для окончательного вывода нужно проверить достаточное условие.

Во втором уравнении системы H = 2 (y₁ и y₂) и D = 1 (x₄). Выполняется равенство D+1 = H, т.е. 1+1=2. Уравнение скорее всего идентифицируемо.

В третьем уравнении системы H = 3 (y₁, y₂, y₃), а D=2 (x₁ и x₂). Следовательно, по счетному правилу D+1 = H, и это уравнение скорее всего идентифицируемо. Таким образом, система в целом удовлетворяет необходимому условию идентифицируемости.