Метод наименьших квадратов. Статистические свойства оценок

Для определения коэффициентов регрессии 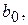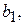..., 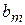используется метод наименьших квадратов (МНК). В соответствии с МНК минимизируется сумма квадратов остатков:

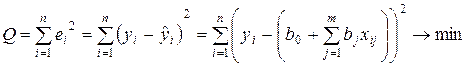. (2.1.7)

Учитывая, что произведение

,

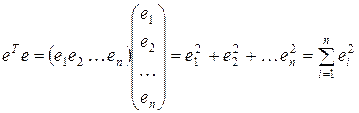условие (2.1.7) может быть записано в виде:

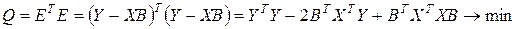. (2.1.8)

Необходимым условием минимума функции 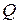является равенство нулю всех ее частных производных по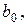 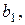..., , 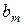т. е. равенство нулю вектора частных производных :

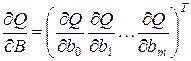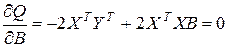, (2.1.9)

откуда получаем систему нормальных уравнений в матричной форме для определения вектора B:

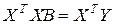. (2.1.10)

Если предпосылка 6 регрессионного анализа выполнена, то ранг матрицы 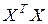равен m+1, т. е. матрица является невырожденной (ее определитель не равен нулю), и существует обратная матрица 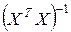. Поэтому решением системы (2.1.10) является вектор МНК-оценок коэффициентов регрессии

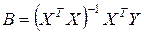. (2.1.11)

Пример 2.1.1

Имеются следующие данные по темпам прироста заработной платы 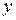(%), производительности труда 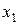(%), а также уровню инфляции (%):

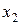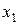
	3,5 2,8 6,3 4,50 3,1 1,5
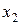
	4,5 3 3,1 3,8 3,8 1,1
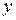
	9 6 8,9 9 7,1 3,2

Оценить по МНК уравнение регрессии .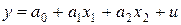

Решение. МНК-оценку вектора параметров модели вычислим по формуле (2.1.11):

,

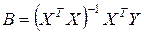где 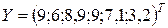– вектор-столбец результативной переменной,

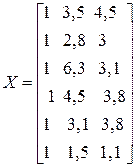
– матрица значений факторных переменных. Вычислим последовательно

, .

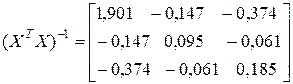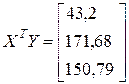Таким образом, вектор коэффициентов равен

,

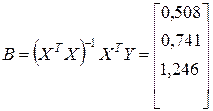и следовательно, уравнение регрессии имеет вид

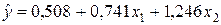. (2.1.12)

Выражение (2.1.11) для вектора оценок параметров регрессии можно представить в эквивалентном виде:

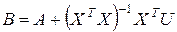, (2.1.13)

откуда получаем статистические характеристики коэффициентов регрессии.

1. Математическое ожидание:

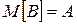. (2.1.14)

2. Ковариационная матрица

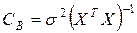. (2.1.15)

Теорема Гаусса-Маркова. Если регрессионная модель (2.1.1) удовлетворяет условиям 1-4, 6, то оценка метода наименьших квадратов 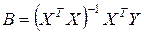является наиболее эффективной, т. е. имеет наименьшую дисперсию в классе линейных несмещенных оценок.

Несмещенная оценка 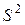дисперсии ошибки 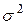случайного члена 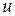(или остаточная дисперсия) определяется выражением

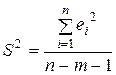. (2.1.16)

Несмещенная оценка матрицы ковариации вектора коэффициентов B получается путем замены в (2.1.15) неизвестного значения дисперсии ошибки его оценкой (2.1.16):

,

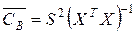откуда следует, что несмещенные оценки дисперсий коэффициентов 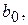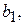..., 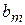находятся по формуле

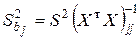. (2.1.17)

Здесь 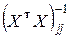– j -й диагональный элемент матрицы .

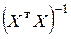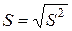называется стандартным отклонением регрессии, 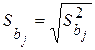называется средним квадратическим отклонением (стандартной ошибкой) коэффициента регрессии .

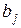Пример 2.1.2

По данным примера 2.1.1 оценить стандартные ошибки регрессии и коэффициентов регрессии.

Решение. Несмещенная оценка дисперсии возмущений для множественной регрессии вычисляется по формуле (2.1.16). Поэтому необходимо вычислить значения остатков для всех наблюдений. Расчетные значения 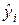определим по уравнению регрессии (2.1.12). Результаты разместим в третьем столбце табл. 2.1.1.

В четвертом и пятом столбцах размещены значения остатков и квадратов остатков.

Таблица 2.1.1

№ п.п.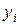
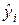
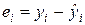
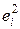
		8,713	0,287	0,082
		6,324	-0,324	0,105
	8,9	9,045	-0,145	0,021
		8,582	0,418	0,175
	7,1	7,544	-0,444	0,197
	3,2	2,992	0,208	0,043
Сумма	0,623

Оценка дисперсии возмущения будет равна

,

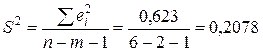а оценка стандартной ошибки возмущения равна

.

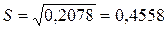Вычислим дисперсии коэффициентов регрессии через диагональные элементы ковариационной матрицы (2.1.15):

.

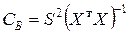
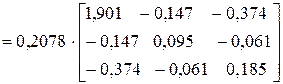Таким образом,

,

,

.

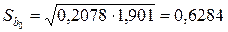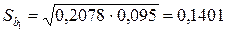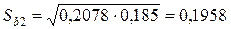Вопросы для самопроверки

1. Как определяется модель множественной линейной регрессии?

2. Сформулируйте задачу регрессионного анализа в матричном виде.

3. Перечислите условия Гаусса-Маркова для классической линейной модели множественной регрессии.

4. Какая матрица называется ковариационной матрицей возмущений?

5. В чем суть МНК-оценки параметров множественной линейной регрессии?

6. Приведите формулу расчета коэффициентов уравнения множественной регрессии в методе наименьших квадратов.

7. Опишите алгоритм определения коэффициентов множественной линейной регрессии по МНК в матричной форме.

8. Какими свойствами обладают МНК-оценки?

9. Сформулируйте теорему Гаусса-Маркова.

10. Приведите формулы расчета дисперсий и стандартных ошибок коэффициентов регрессии.

2.2. Оценка качества модели

Изучаемые вопросы:

§ проверка гипотез о параметрах регрессии;

§ интервальные оценки параметров регрессии;

§ проверка общего качества уравнения регрессии.

При работе с теоретическим материалом следует разобрать примеры решения задач и ответить на контрольные вопросы, приведенные в конце темы.

Поскольку уравнение регрессии определяется на основе выборочных данных, то коэффициенты этого уравнения являются точечными оценками (случайными величинами), значения которых изменяются от выборки к выборке. А значит, необходима проверка значимости этих коэффициентов.

Для оценки статистической значимости коэффициентов регрессии рассчитывают доверительные интервалы и t -критерии.