Производная по направлению

При изучении скалярного поля методами анализа мы должны в первую очередь описать его локальные свойства, т. е. изменение величины U (М) при переходе от данной точки М к близким точкам. Для этого мы используем производную поля по направлению. Напомним это понятие.

Пусть U (М)- скалярное поле. Рассмотрим две близкие точки М и М ' и составим отношение

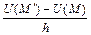(2)

где h - длина отрезка ММ '.

Пусть точка М ' приближается к М, причем направление отрезка ММ ' все время совпадает с направлением фиксированного единичного вектора l. Если при этом отношение (2) стремится к некоторому пределу, то этот предел называется производной скалярного поля U (М) в точке М по направлению l и обозначается:

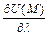Производная 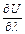характеризует скорость изменения величины U (М),

в направлении l.

Для вычисления 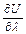выберем некоторую систему координат и представим U (М) в виде U (х, у, z).

Пусть направление l образует с осями координат углы a, b, g. Тогда

ММ ' = h (i cos a+ j cos b +k cos g)

U (М ') = U (х + h cos a, у + h cos b, z + h cos g), (З)

а производная 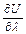совпадает с производной по h от сложной функции (3) при h = 0. Дифференцируя, получаем:

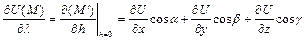(4)

1.1.5. Градиент скалярного поля.

Выражение (6.4) можно рассматривать как скалярное произведение двух векторов:

единичного вектора

l = (cos a, cos b, cos g),

определяющего направление, по которому берется производная 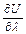и вектора, имеющего компоненты

, ,

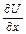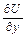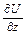
Этот вектор называется градиентом скалярного поля U и обозначается символом grad U.

Таким образом,

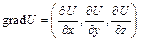(5)

и, следовательно,

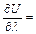
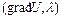(6)

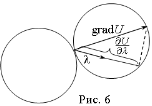
Рис. 6 дает наглядную интерпретацию выражения производной по направлению как проекции grad U на это направление.

Из формулы (6), которую можно переписать в виде

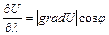
и (где j - угол между grad U и единичным вектором l), видно, что в каждой точке. в которой grad U ¹ 0, существует единственное направление, по которому 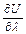имеет наибольшее значение, т. е. единственное направление наибыстрейшего возрастания функции U. Это

направление совпадает с направлением вектора grad U. Действительно, для этого направления j = 0 и, следовательно,

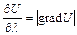в то время как для всех других направлений

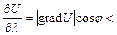
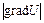
Итак, мы получили, что направление вектора grad U - это направление наибыстрейшего возрастания величины U, а длина вектора grad U равна скорости возрастания величины U в этом направлении.

Однако ни направление наибыстрейшего возрастания функции, ни величина ее производной в этом направлении не зависят, очевидно, от выбора системы координат. Мы установили, таким образом, что градиент скалярного поля зависит лишь от самого поля, но не от выбора системы координат (хотя из равенства (5), принятого нами за определение градиента, это сразу и не видно).

Производные 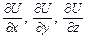в данной точке М - это компоненты вектора, нормального к поверхности U (х, у, z) = const, проходящей через эту точку. Таким образом, в каждой точке поля U градиент поля направлен по нормали к поверхности уровня, проходящей через эту точку.

Назовем линией градиента скалярного поля и всякую кривую, касательная к которой в каждой ее точке направлена по grad U в этой же точке. Таким образом, линии градиента поля - это те линии, вдоль которых поле U меняется быстрее всего.

Можно показать, что если функция U (х, у, z) имеет непрерывные частные производные до 2-го порядка включительно, то через каждую точку области, в которой задано поле U, проходит одна и только одна линия градиента. В каждой точке линия градиента ортогональна той поверхности уровня, на которой эта точка лежит.

Лекция 2

1.2. Векторные поля

1.2.1. Определение и примеры векторных полей.

Мы говорим, что, в некоторой области W определено векторное поле, если каждой точке М этой области поставлен в соответствие определенный вектор А (М).

Один из важных примеров векторных полей, к которому мы будем неоднократно возвращаться, - это поле скоростей стационарного потока жидкости. Оно определяется так: пусть область W заполнена жидкостью, текущей в каждой точке с некоторой скоростью v, не зависящей от времени (но различной, вообще говоря, в разных точках); поставив в соответствие каждой, точке М из W вектор v = v (М), мы получим векторное поле, называемое полем, скоростей.

Другой важный пример векторного поля - это поле тяготения. Пусть в пространстве распределена некоторая масса. Тогда на материальную точку с массой 1, помещенную в данную точку М, действует некоторая гравитационная сила. Эти силы, определенные в каждой точке, образуют векторное поле, называемое полем тяготения (отвечающим данному распределению масс) или гравитационным полем.

Если в пространстве распределены каким-либо образом электрические заряды, то на единичный электрический заряд, помещенный в точку М, эти заряды действуют с определенной силой F (М). Образуемое этими силами векторное поле называется электростатическим полем.

И поле тяготения, и электрическое поле представляют собой примеры силовых полей.

Если А (М) - некоторое векторное поле в пространстве, то, взяв в этом пространстве какую-либо декартову систему координат, мы можем представить А (М) как совокупность трех скалярных функций компонент этого вектора. Эти компоненты мы будем обозначать, как правило, Р (х, у, z), Q (x, у, z) и R (x, у, z). В дальнейшем мы будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.

1.2.2. Векторные линии и векторные трубки.

Пусть в области W задано векторное поле А (М). Кривая L, лежащая в W, называется векторной линией если в каждой точке этой кривой направление (касательной к ней совпадает с направлением вектора А в этой же точке. В частности, если поле А есть поле скоростей стационарного потока жидкости, то его векторные линии - это траектории частиц жидкости.

В вопросах связанных с изучением полей, важную роль играет задача о нахождении векторной линии поля А, проходящей через данную:точку М ₀.

Аналитически эта задача формулируется, очевидно, так: требуется найти вектор-функцию r (t), удовлетворяющую условиям

r ' (t) = l А,

r (t ₀) = r ₀(7)

где r ₀- радиус-вектор начальной точки М ₀,

t ₀ - начальный момент времени,

l - произвольная числовая величина.

Можно показать, что если компоненты Р, Q, R вектора А непрерывно дифференцируемые функции координат ни в одной точке не обращающиеся в нуль одновременно, то условия (7) действительно определяют в той области, в которой задано поле А, одну и только одну векторную линию.

Ограниченная некоторой поверхностью S часть пространства, в котором задано векторное поле А, называется векторной трубкой, если в каждой точки поверхности S нормаль к S ортогональна вектору А в этой же точке. Иначе говоря, векторная трубка - это часть пространства состоящая из целых векторных линий; каждая векторная линия или целиком лежит внутри данной векторной трубки, или находится целиком вне ее. Можно сказать, что поверхность S, ограничивающая векторную трубку, соткана из векторных линий.

Если снова представить себе векторное поле А как поле скоростей движущейся жидкости, то векторная трубка - это та часть пространства, которую «заметает» при своем перемещении некоторый фиксированный объем жидкости.

1.2.3. Различные виды симметрии векторных полей.

Изучение векторного поля (как и скалярного) существенно облегчается, если это поле обладает теми или иными свойствами симметрии. Перечислим некоторые важнейшие частные случаи.

а) Плоскопараллельное поле.

Если для данного векторного поля А можно подобрать декартову систему координат. в которой компоненты поля А имеют вид Р (х, у), Q (х, у), R (х, у) (т. е. не зависят от z), то поле А называется плоскопараллельным.

Если при этом R (х, у) = 0, то поле А называется плоским. Примером такого поля может служить поле скоростей жидкости, скорости частиц которой параллельны некоторой фиксированной плоскости и не зависят от расстояния частицы до данной плоскости (плоский поток). Векторные линии такого поля - плоские кривые (одни и те же в каждой параллельной плоскости).

б) Осесимметричекое поле.

Векторное поле А называется осесимметрическим, если существует такая цилиндрическая система координат r, j, z, что в каждой точке М вектор А (М) зависит лишь от r и z, но не от j. Иными словами такое поле переходит само в себя при повороте вокруг оси z.

Если вектор А (М) зависит только от r, то поле называется цилиндрическим.

в) Одномерное поле.

Векторное поле называется одномерным. если существует такая декартова система координат, в которой компоненты этого поля имеют вид Р (х, у), 0, 0. Векторные линии такого поля представляют собой, очевидно, совокупность всех прямых, параллельных оси х.

1.2.4. Поле градиента. Потенциальное поле.

Рассмотрим снова некоторое скалярное поле U (М). Построив в каждой точке М вектор grad U, мы получим векторное поле - поле градиента скалярной величины U. Введем следующее:

Определение. Векторное поле А (М) называется потенциальным, если его можно представить как (градиент некоторого скалярного поля U (М):

A = grad U.

Само скалярное поле U называется при этом потенциалом векторного поля А.

Рассмотрим следующий пример.

Пусть U = f (r), где 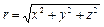(т. е. U - cсферическое поле). Найдем grad U.

Имеем

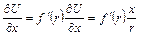Аналогично

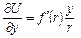и .

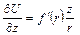Таким образом,

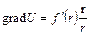r = x i + y j + z k. (8)

Если векторное поле А имеет потенциал, то этот потенциал определяется полем А однозначно, с точностью до произвольного постоянного слагаемого. Действительно, если скалярные поля U и V имеют один и тот же градиент, то

grad (U - V) º 0.

Но тогда и производная от U - V по любому направлению равна нулю в любой точке, откуда сразу следует, что

U - V = const.

Векторные линии потенциального поля А представляют собой, разумеется, линии градиента его потенциала U, т. е. линии наибыстрейшего изменения этого потенциала.

Естественно возникает вопрос об условиях, при которых данное векторное поле А потенциально. Действительно, выражение

P dx + Q dy + R dz

(где Р, Q, R - непрерывные функции, имеющие непрерывные частные производные l-го порядка) служит полным дифференциалом некоторой однозначной функции U (х, у, z) в том и только том случае, если Р, Q, R удовлетворяют условиям:

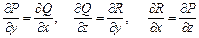(9)

Но если

P dx + Q dy + R dz = dU,

то

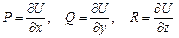
т. е. условие (9) как раз и означает, что поле (Р, Q, R) потенциально.

Итак, для того чтобы векторное поле А = (Р, Q, R), имеющее непрерывные и непрерывно дифференцируемые компоненты, было потенциальным необходимо и достаточно, чтобы выполнялись равенства (9).

Если А - потенциальное векторное поле, то фактическое нахождение его потенциала сводится к нахождению функции по ее полному дифференциалу

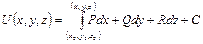
а для двух переменных

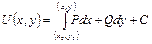
к понятию потенциального поля мы еще вернемся.

Пример. Пусть в начало координат О помещена масса т. Если теперь в некоторую точку М (х, у, z) поместить единичную массу, то на нее будет действовать сила притяжения равная

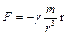
(r = x i + y j + z k).

Эти силы, определяемые в каждой точке пространства, образуют векторное поле - поле тяготения точечной массы т. Его можно представить как градиент скалярной величины

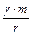
называемой ньютоновским потенциалом точечной массы т. В самом деле, воспользовавшись формулой (8), получаем

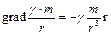Лекция 3

1.3. Поток векторного поля. Дивергенция

1.3.1. Поток векторного поля через поверхность.

Количество жидкости, протекающей за единицу времени через данную (ориентированную) поверхность S равно интегралу

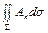
где А_п - нормальная составляющая вектора скорости А = (Р, Q, R).

Эту величину мы назвали потоком жидкости через поверхность S. Пусть теперь А - произвольное векторное поле и S - ориентированная поверхность. Поверхностный интеграл

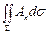
мы назовем потоком векторного поля, А через поверхность S. Таким образом, если А - скорость движения жидкости, то поток вектора А через некоторую поверхность равен количеству жидкости протекающей через эту поверхность за единицу времени. Для векторного поля иной природы поток имеет, конечно, другой физический смысл.

При м е р. Пусть U = U (х, у, z) - поле температур внутри некоторого тела, k - коэффициент теплопроводности и А = grad U. Согласно закону Фурье, количество тепла dQ, протекающее за единицу времени через элемент ds некоторой поверхности S, выражается формулой

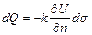, (10)

где 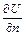- производная поля температур в направлении нормали к ds. (Знак минус в правой части равенства (10) отвечает тому известному факту, что тепло течет от более нагретых частей тела к менее нагретым, т. е. в направлении убывания U.) Так как

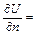
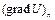то равенство (10) можно переписать в виде

dQ = - k (grad U) _п d s,

из которого следует, что количество тепла Q, протекающего за единицу времени через всю поверхность S, равно

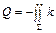
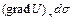. (11)

Введя вектор

q = - k grad U,

называемый вектором потока тепла, получаем

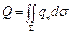
Таким образом, количество тепла, протекающее через S за единицу времени, равно потоку вектора q через поверхность S (отсюда и название «вектор потока тепла»).

1.3.2. Дивергенция

Пусть А - некоторое векторное поле, которое мы снова будем представлять себе как поле скоростей несжимаемой жидкости. Поскольку жидкость несжимаема, поток

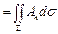
вектора А через какую-либо замкнутую поверхность S равен, очевидно, количеству жидкости, которое за единицу времени возникает или уничтожается в пределах той пространственной области W, границей которой служит S. Назовем это количество суммарной мощностью источников (если П > 0) или стоков (если П < 0), расположенных в области S. Рассмотрим отношение

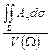
потока жидкости через поверхность S к объему области W, ограниченной этой поверхностью. Оно представляет собой среднюю плотность источников (или стоков), т. е. количество жидкости, возникающей (исчезающей) за единицу времени в единице объема области W.

Рассмотрим, наконец, предел

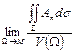
этого отношения, где знак 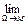означает предел при условии, что область W стягивается к некоторой фиксированной точке М. Этот предел можно назвать плотностью источников (стоков) в точке М. Он представляет собой скалярную величину и служит важной характеристикой исходного поля.

Рассмотрев этот пример, перейдем к общим определениям.

Пусть А - некоторое векторное поле. Поставим в соответствие каждой пространственной области W, ограниченной гладкой или кусочно-гладкой поверхностью S, величину

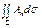
- поток вектора А через внешнюю сторону S. Мы получим некоторую функцию области Ф (W). Легко проверить, что эта функция аддитивна.

Определение. Производная функции Ф (W) по объему, т.е. предел

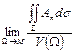(12)

называется - дивергенцией векторного поля А и об означается

div А.

Таким образом, введенная нами для поля скоростей несжимаемой жидкости плотность источников представляет собой дивергенцию

этого поля скоростей.

Теорема 1. Если А = (Р, Q, R) - векторное поле, определенное в области W и такое, что функции Р, Q, R непрерывны в W вместе со всеми своими первыми производными, то div A существует во всех точках этой области и в любой декартовой системе координат выражается формулой

div А 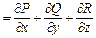(13)

Доказательство. Воспользуемся формулой Остроградского

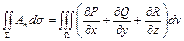В силу теоремы о производной тройного интеграла по объему, производная по объему от правой части этого равенства существует и равна 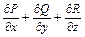. Следовательно, тому же самому выражению равна и производная по объему от левой его части. Но эта последняя и есть по определению div А.

3амечание. Часто равенство

div А =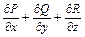

принимают за определение дивергенции. Однако это определение менее удобно, чем принятое нами, так как оно опирается на выбор той или иной системы координат, и мы должны еще доказывать, что сумма

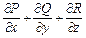
от выбора системы координат не зависит.

А независимость от выбора системы координат выражения (12) очевидна.

Итак, каждому векторному полю А, компоненты которого непрерывны и имеют непрерывные частные производные, мы поставили в соответствие скалярную функцию div А. Пользуясь этим понятием, мы можем теперь формулу Остроградского записать так:

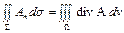(14)

т. е. поток вектора А через внешнюю сторону замкнутой поверхности S равен интегралу от дивергенции поля А, взятому по области, ограниченной поверхностью S.

Лекция 4

1.3.3. Физический смысл дивергенции для различных полей.

Примеры.

а) Мы уже выяснили, что для поля скоростей А несжимаемой жидкости, движущейся в некоторой пространственной области, выражение

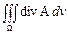
представляет собой суммарную мощность источников расположенных в области W, а div А - это плотность источников (т. е. их мощность, приходящуюся на единицу объема). В частности, если А поле скоростей несжимаемой жидкости, у которой нет ни стоков, ни источников, то

div A = 0.

б) Рассмотрим теперь поле тяготения, создаваемое некоторым распределением масс. Выясним, что представляет собой дивергенция такого поля. Рассмотрим сначала поле, создаваемое массой т ₀, сосредоточенной в точке (х ₀, у ₀, z ₀). В этом случае единичная масса, помещенная в точку (х, у, z), притягивается с силой

F 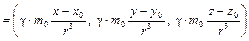(15)

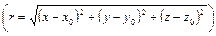
Здесь g - постоянная тяготения, зависящая от выбора единиц. Впредь мы g писать не будем, считая, что система единиц выбрана так, что g = 1. Вычислим дивергенцию силового поля (15). В каждой точке, отличной от точки (х ₀, у ₀, z ₀), имеем

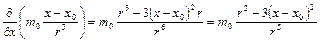аналогично

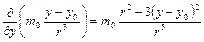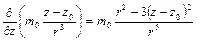Складывая, получаем

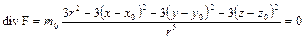
Однако в точке (х ₀, у ₀, z ₀) приведенные выкладки теряют смысл и в этой точке значение div F вообще не определено. Поэтому и значение интеграла

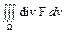
не может быть получено непосредственным вычислением, если область W содержит точку (х ₀, у ₀, z ₀). Таким образом, выражение, стоящее в формуле Остроградского (14) справа, в нашем случае не определено. Однако мы легко можем найти величину, стоящую в этой формуле слева, т. е. поток вектора F через поверхность S, ограничивающую объем W. Сделаем это. Пусть сначала S - сфера некоторого радиуса а с центром в точке (х ₀, у ₀, z ₀). В каждой точке такой сферы направление вектора, (15) совпадает с направлением нормали к этой сфере. Поэтому проекция вектора (6.15) на нормаль в данном случае равна длине этого вектора, т. е. постоянной величине 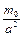. Следовательно,

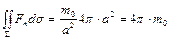Заменив сферу S любой другой замкнутой поверхностью S₁ охватывающей точку (х ₀, у ₀, z ₀), мы получим тот же самый результат.

Действительно, выберем сферу S настолько малой, чтобы она целиком содержалась внутри S₁. Тогда

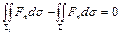так как левая часть этого равенства представляет собой поток вектора F через границу пространственной области, в которой

div F º 0.

Следовательно,

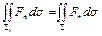Рассмотрим теперь поле тяготения, создаваемое несколькими точечными массами. Это поле равно сумме полей, создаваемых каждой массой в отдельности. Поток суммы полей через некоторую поверхность S равен, очевидно, сумме потоков слагаемых; отсюда вытекает, что поток через некоторую замкнутую поверхность поля тяготения, создаваемого системой материальных точек, равен сумме находящихся внутри этой поверхности масс, умноженной на 4p.

С помощью предельного перехода от системы материальных точек к массе, непрерывно распределенной по пространству с объемной плотностью r (х, у, z), можно показать, что при непрерывном распределении масс поток гравитационного поля через замкнутую поверхность S равен заключенной внутри этой поверхности массе, умноженной на 4p. Но эта же масса может быть представлена как интеграл от плотности r (х, у, z), взятый по объему W, ограниченному поверхностью S. Таким образом, обозначая по-прежнему символом F (х, у, z) значение гравитационного поля в точке (х, у, z), имеем

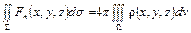
откуда

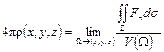стоящий здесь справа предел представляет собой дивергенцию векторного поля F. Итак, окончательно получаем: дивергенция гравитационного поля, создаваемого некоторым распределением масс, равна объемной плотности r (х, у, z) этого распределения, умноженной на 4p.

в) Те же самые рассуждения, которые мы провели для поля тяготения, можно повторить и для электростатического поля и показать, что дивергенция такого поля равна плотности зарядов, умноженной на 4p. (Это утверждение, известное в электростатике под названием теоремы Гаусса, широко используется в различных задачах, связанных с электростатическими полями, например при вычислении напряженности поля в конденсаторах различной формы.)

Лекция 5

1.3.4. Соленоидальное поле.

Векторное поле, дивергенция которого тождественно равна нулю, называется соленоидальным или трубчатым. Примером соленоидального поля может служить, как мы рассматривали ранее, поле скоростей несжимаемой жидкости при отсутствии стоков и источников, т.е. при условии, что ни в одной точке жидкость не исчезает и не возникает.

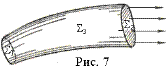Для соленоидальных полей имеет место так называемый закон сохранения интенсивности векторной трубки, состоящий в следующем. Пусть А - соленоидальное поле. Рассмотрим некоторую векторную трубку и возьмем ее отрезок, заключенный между двумя ее сечениями S₁ и S₂ (рис. 7). Эти сечения вместе с боковой поверхностью S₃ трубки образуют замкнутую поверхность S. Так как поле соленоидально, т. е. div А º 0, то, в силу формулы Остроградского,

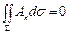Но

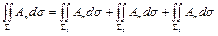, (16)

причем в каждом из слагаемых имеется в виду внешняя сторона поверхности. Третье из стоящих справа слагаемых равно нулю, так как по определению векторной трубки на поверхности S₃ направление векторного поля А перпендикулярно направлению нормали к этой поверхности, т. е. на S₃

А_n º 0.

Если мы теперь на сечении S₁ направление нормали изменим на противоположное, то равенство (16) перепишется в виде

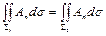, (17)

т. е. поток вектора А через любое сечение векторной трубки имеет одно и то же значение. Если поле вектора А представлять себе как поле скоростей несжимаемой жидкости при отсутствии источников и стоков, то равенство (17) означает: количество жидкости, протекающей за единицу времени через сечение векторной трубки, одно и то же для всех сечений этой трубки.

1.3.5. Уравнение неразрывности.

В качестве применения изложенных ранее понятий дадим вывод одного из основных уравнений движения жидкости, так называемого уравнения неразрывности. Пусть А - поле скоростей движущейся жидкости. Мы будем предполагать, что в рассматриваемой области жидкость не исчезает и не возникает. Однако в отличие от наших предыдущих рассмотрений мы будем предполагать эту жидкость сжимаемой, т. е. считать плотность r некоторой функцией координат х, у, z и времени t. Выясним, как связана скорость движения такой жидкости с изменением ее плотности. Для этой цели рассмотрим некоторый замкнутый объем W и подсчитаем двумя способами изменение D Q количества жидкости внутри этого объема за время D t. Пусть r (х, у, z) - плотность жидкости в момент t в точке х, у, z. Тогда, очевидно,

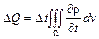с другой стороны, изменение количества жидкости внутри объема W равно умноженному на Dt потоку жидкости через поверхность S, ограничивающую этот объем, т.е. равно

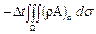где n - наружная нормаль (знак минус берется потому, что если скорость направлена наружу, то количество жидкости в объеме уменьшается). Преобразовав этот поверхностный интеграл с помощью формулы Остроградского в объемный, получим

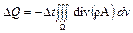
Приравняв друг другу два выражения для D Q и сократив на D t, будем иметь

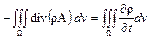
так как это равенство должно иметь место для любой области W, то равны между собой и подынтегральные выражения, т. е.

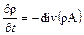. (18)

Мы получили уравнение, связывающее между собой скорость и плотность движущейся жидкости при отсутствии источников и стоков. Оно называется уравнением неразрывности.

Если ввести вектор J = rА - плотность потока жидкости, то уравнение неразрывности можно переписать так:

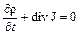. (18')

1.3.6. Плоское течение жидкости.
Формула Остроградского на плоскости.

Рассмотрим плоское векторное поле, т. е. поле, компоненты которого в некоторой декартовой системе координат имеют вид

Р = Р (х, у), Q = Q (x, у), R = 0 (19)

Его можно представлять себе как поле скоростей жидкости, каждая частица которой движется параллельно фиксированной плоскости со скоростью, не зависящей от ее расстояния до этой плоскости (такое движение жидкости называется плоским течением). Дивергенция такого поля равна

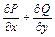
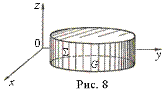
Пусть W - цилиндр высоты единица, с основанием G, лежащим в плоскости ху, и боковой поверхностью S (рис. 8). Напишем для области W формулу Остроградского, предварительно заметив, что тройной интеграл от 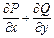по W численно равен двойному интегралу от этого выражения по плоской области G, поток вектора (19) через поверхность S равен криволинейному интегралу

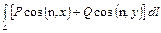
где n - нормаль к контуру L, а поток через верхнее и нижнее основания цилиндра W равен нулю (последнее вытекает из того, что вектор (19) перпендикулярен оси z). В силу сказанного, формула Остроградского для плоскопараллельного поля А и цилиндрической области W имеет вид

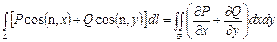. (20)

Отбросим теперь окончательно третью координату z, будем рассматривать (19) как векторное поле, заданное в плоскости ху. Назовем криволинейный интеграл

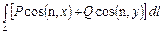(21)

потоком этого векторного поля через контур L. Тогда формула (20), называемая формулой Остроградского для плоскости, означает, что двойной интеграл от дивергенции плоского поля А по некоторой области G равен потоку вектора А через границу этой области.

Легко убедиться в том, что формула (20) - просто эквивалент формулы Грина. Действительно, если мы, как обычно обозначим через а угол между касательной к кривой и положительным направлением оси х, то

cos (n, х) = - sin a, cos (n, у) = cos a,

поэтому интеграл (21) можно записать так:

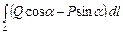или

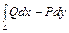Преобразовав этот криволинейный интеграл в двойной с помощью формулы Грина, мы и получим равенство (20). Это рассуждение можно обратить, т. е. если равенство (20) установлено, то из него можно вывести формулу Грина.

Таким образом, как формула Стокса, так и формула Остроградского в плоском случае превращаются в формулу Грина.

Лекция 6

1. 4. Циркуляция. Ротор

1.4.1. Циркуляция векторного поля.

Пусть снова А = (Р, Q, R) некоторое векторное поле и L - гладкая или кусочно-гладкая кривая. Криволинейный интеграл

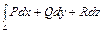
или, короче,

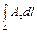
где А _t - тангенциальная составляющая поля А на контуре L, мы назовем циркуляцией векторного поля А вдоль кривой L.

Если А = (Р, Q, R) - силовое поле, то его циркуляция вдоль кривой L представляет собой, работу этого силового поля вдоль пути L. Для полей иной природы циркуляция имеет, конечно, другой физический символ.

1.4.2. Ротор векторного поля.
Формула Стокса и ее запись в векторных обозначениях.

Если L - замкнутый контур, то криволинейный интеграл

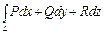
по этому контуру можно преобразовать в поверхностный, воспользовавшись формулой Стокса:

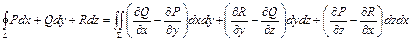
(22)

взятый по некоторой поверхности S, натянутой на контур L. Правая часть равенства (22) представляет собой поток через поверхность S вектора

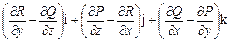. (23)

Назовем этот вектор рота ром (или вихрем) векторного поля А и обозначим rot А. Таким образом, по определению

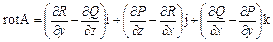. (24)

Пользуясь понятием ротора, мы можем переписать формулу Стокса в следующем компактном виде:

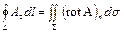(25)

т. е. циркуляция векторного поля А вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность, натянутую на этот контур.

В нашем определении ротора участвует не только само векторное поле А, но и некоторая определенная система координат (х, у, z). Однако на самом деле вектор rot А не зависит от выбора координатной системы, а определяется лишь исходным векторным полем А. Чтобы убедиться в этом, воспользуемся формулой Стокса (25), считая, что поверхность S - это некоторая плоская площадка, а L – ограничивающий ее контур. Применив к стоящему в равенстве (25) справа поверхностному интегралу теорему о среднем, получим

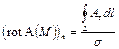где М - некоторая точка, принадлежащая площадке S, а s - площадь этой площадки. Будем теперь стягивать площадку S к некоторой фиксированной точке М так, чтобы направление нормали n к этой площадке оставалось все время одним и тем же. В пределе получим

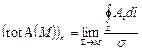. (26)

Циркуляция вектора А вдоль контура не зависит от выбора координатной системы, поэтому из равенства (26) вытекает, что проекция rot А на направление нормали n не зависит от выбора системы координат. Но направление нормали n мы могли выбрать произвольно, поэтому проекция вектора rot А на любое направление, а следовательно, и сам вектор rot А не зависят от выбора системы координат.

1.4.3. Символическая запись ротора.

Ротор векторного поля А = (Р, Q, R) удобно записывать в виде символического детерминанта

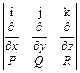(27)

где i, j, k - единичные векторы, направленные по осям координат, а под умножением символа 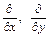или 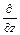на некоторую функцию понимается выполнение соответствующей операции дифференцирования (например, 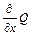означает ).

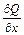Действительно, разложив детерминант (27) по элементам первой строки, получим, что

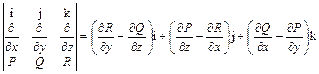
Лекция 7

1.4.4. Физический смысл ротора.

Физический смысл ротора можно пояснить следующим образом. Будем снова рассматривать векторное поле А как поле скоростей движущейся жидкости. Поместим в таком потоке, в определенной его точке, бесконечно малое колесико с лопастями, расположенными по окружности L этого колесика (рис. 9). Под воздействием потока жидкости такое колесико будет вращаться с некоторой скоростью, зависящей, вообще говоря, от направления оси колесика.

Естественно считать, что линейная скорость каждой точки окружности L по величине будет равна среднему произведений проекций вектора А на направление касательной к L, т. е. будет выражаться формулой

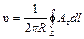. (28)

По формуле Стокса (25) криволинейный интеграл (28) можно преобразовать в поверхностный интеграл

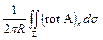, (29)

взятый по площади S рассматриваемого колесика. Считая это колесико бесконечно малым, мы можем записать интеграл 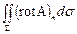в виде произведения площади колесика на значение (rot А) _п в его центре, т. е. в виде

p R ² (rot А) _п

В результате равенство (28) принимает вид

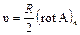
Максимально возможное значение проекции вектора на какое-либо направление есть модуль этого вектора. Поэтому, если направление оси колесика выбрать так, чтобы его скорость v была максимальной (это направление, очевидно, совпадает с направлением rot А), то мы получим

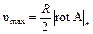
или

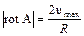
Но 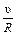- это величина угловой скорости w колесика. Итак, мы получили следующий результат: если колесико с лопастями ориентировано так, что скорость его вращения максимальна, то его угловая скорость равна половине ïrot А ï, а направление оси совпадает с направлением вектора rot А.

Таким образом, rot А характеризует «вращательную компоненту» поля скоростей; он равен удвоенной угловой скорости вращения бесконечно малой частицы жидкости.

Примеры. 1. Рассмотрим векторное поле с компонентами

P = - y w, Q = x w, R = 0.

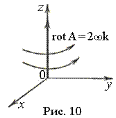Это поле можно рассматривать как поле скоростей, отвечающее вращению всего пространства вокруг оси z с угловой скоростью w. Ротор этого векторного поля равен, как легко проверить, 2wk, т. е. он направлен по оси вращения, а по величине равен удвоенной угловой скорости (рис. 10).

Физический смысл этого результата заключается в следующем. Всякая частица жидкости при вращении вокруг оси z участвует в двух движениях: в мгновенном переносном движении со скоростью V = (-y w, x w, 0) и в мгновенном вращательном движении. Легко видеть, что мгновенная угловая скорость вращения любой частицы совпадает с угловой скоростью w всего макроскопического движения жидкости. Поэтому поле мгновенных угловых скоростей частиц оказывается постоянным и равным w. Значит, и поле ротора также постоянно и равно 2w. Вся жидкость как бы заполнена бесконечно малыми вихрями.

2. Рассмотрим жидкость, текущую в постоянном направлении с постоянной скоростью, т. е, предположим, что Р, Q и R постоянны. В этом случае rot A º 0.

3. Пусть Р = у, Q = 0, R = 0. В этом случае

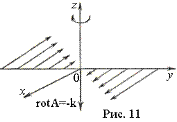rot А = - k.

В последнем примере ротор в каждой точке отличен от нуля, хотя все векторные линии - прямые, параллельные плоскости yz. Это может показаться противоречащим утверждению, что rot А характеризует «вращательную компоненту» поля А. Но на самом деле это не так. Здесь «вращательная компонента» обусловлена не искривлением векторных линий, а изменением скорости движения при изменении расстояния от плоскости yz. Легко сообразить, что колесико с лопастями, поставленное в поток жидкости, движущейся в каждой точке (х, у, z) со скоростью (у, 0, 0), не будет находиться в покое, если только его ось вращения не перпендикулярна оси z.

4. Пусть векторное поле А имеет компоненты:

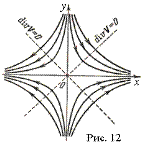
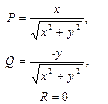(30)

Это поле можно рассматривать как поле скоростей жидкости, движущейся в плоскости ху по гиперболам ху = С (рис. 12) так, что величина скорости в каждой точке равна 1. Найдем дивергенцию и ротор этого поля. Имеем:

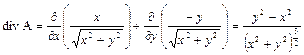
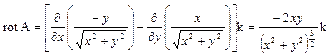
Здесь дивергенция. положительна, когда |у|>|х|, и отрицательна при |у|<|х|. Физически это означает, что движение несжимаемой жидкости, описываемое полем (30), возможно лишь тогда, когда в тех областях, где ïуï>ïхï, имеются источники, а там, где |у|<|х| имеют место стоки. Ротор поля (30), как и всякого плоскопараллельного поля, направлен в каждой точке по оси z, именно его направление совпадает с положительным направлением оси z во второй и четвертой четвертях и с отрицательным направлением оси z в первой и третьей. И дивергенция, и ротор поля (30) стремятся к нулю, когда х ²+ y ² →¥, т. е. по мере удаления от начала координат.

1.4.5. Еще раз о потенциальных и соленоидальных полях.

Рассматриваемое понятие ротора, непосредственно связано с определениями потенциального и соленоидального полей, введенными ранее.

Мы назвали потенциальным векторное поле, представимое в виде градиента некоторого скалярного поля, и показали, что векторное поле А = (Р, Q, R) потенциально в том и только том случае, если его компоненты удовлетворяют условиям

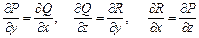Но эти три условия означают не что иное, как равенство нулю всех трех компонент ротора поля А. Таким образом:

Для того чтобы векторное поле А было потенциальным, необходимо и достаточно чтобы выполнялось условие:

rot А º 0.

Понятие соленоидального поля, тоже связано с понятием ротора. Действительно, непосредственное вычисление показывает, что для любого векторного поля А:

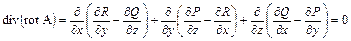
т. е. векторное поле, представимое в виде ротора какого-либо другого векторного поля, соленоидально. Можно показать (мы не будем этого делать), что верно и обратное, т. е. что всякое соленоидальное поле можно представить в виде ротора некоторого векторного поля. Иными словами, для всякого поля А, удовлетворяющего условию
div А = 0, можно подобрать поле В так, что А = rot В. Это векторное поле В определяется не однозначно, а с точностью до произвольного слагаемого вида grad U.

Если А = rot В, то поле В называется вектор р -потенциалом поля А. Хотя потенциальные и соленоидальные поля не исчерпывают всех векторных полей, любое векторное поле сводится к комбинации полей этих двух типов. Точнее говоря, можно доказать, что всякое векторное поле А представимо в виде:

А = В + С.

где В потенциально, а С соленоидально.

Лекция 8

1.5. Оператор Гамильтона

1.5.1. Символический вектор Ñ.

Мы уже ввели понятие градиента скалярного поля. Переход от скалярного поля U к grad U можно рассматривать как некоторую операцию, во многом аналогичную по своим свойствам операции дифференцирования, с той, однако, разницей, что дифференцирование переводит скаляр в скаляр, в то время как здесь мы имеем переход от скаляра к вектору. Операцию перехода от U к grad U часто обозначают, следуя Гамильтону, символом Ñ (читается «набла» и называют оператором «набла», или оператором Гамильтона. Таким образом, по определению:

Ñ U = grad U.

Оператор Ñ удобно трактовать как символический вектор с компонентам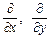и и :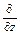

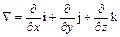а применение его к скалярной функции - как умножение скаляра на этот вектор.

С помощью вектора Ñ удобно записывать и остальные операции векторного анализа, а именно, если А = (Р, Q, R), то

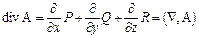т. е. дивергенция векторного поля А есть скалярное произведение символического вектора Ñ и вектора А. Аналогично

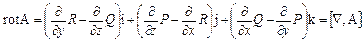
т. е. ротор векторного поля А есть векторное произведение вектора Ñ на вектор А.

1.5.2. Действия с вектором Ñ.

Целесообразность введения символического вектора Ñ состоит в том, что с его помощью удобно получать и записывать различные формулы векторного анализа. Кроме того, сами эти формулы приобретают в такой записи большую наглядность и выразительность. Вот простейшие примеры.

Раньше мы с помощью непосредственных вычислений получили следующие два равенства:

rot grad U = 0

div rot А = 0.

Переписав их с помощью вектора Ñ, получим

[Ñ,Ñ U ] = 0

(Ñ,Ñ, А) = 0.

Левая часть первого из этих равенств представляет собой «векторное произведение» (символическое) двух «векторов», отличающихся друг от друга лишь скалярным множителем, а во втором равенстве слева стоит «смешанное произведение» трех векторов, два из которых одинаковы. Следовательно, равенство нулю этих выражений находится в полном соответствии с основными законами векторной алгебры.

С помощью непосредственной проверки можно убедиться в том, что на вектор Ñ можно перенести многие из основных действий, известных для обычных векторов. Именно это обстоятельство и дает возможность получать с помощью вектора Ñ ряд формул векторного анализа, применяя аппарат векторной алгебры.

Следует, однако, иметь в виду, что аналогия между символическим вектором Ñ и «настоящими» векторами - не полная. Именно, формулы, содержащие символический вектор Ñ, аналогичны обычным формулам векторной алгебры в том случае, если они не содержат произведений переменных величин (скалярных или векторных), т. е. до тех пор, пока нам не приходится применять входящие в Ñ операции дифференцирования к произведению переменных величин. Если же некоторое выражение содержит произведение двух или нескольких переменных сомножителей, то, применяя к этому выражению вектор Ñ, нельзя руководствоваться обычными правилами векторной алгебры. Для установления соответствующих правил действия рассмотрим некоторые примеры.

1. Пусть U = U (х, у, z) - скалярное поле и А = А (х, у, z) - векторное поле. Вычислим div (U А), т. е. (Ñ, U А).

Применение вектора Ñ сводится к применению входящих в него операций дифференцирования. Но, как известно, правило дифференцирования произведения состоит в том, что мы дифференцируем сначала первый сомножитель, а остальные рассматриваем как постоянные, затем дифференцируем второй сомножитель, считая остальные постоянными, и т. д. И берем сумму полученных таким образом выражений.

Условимся каждый раз отмечать в формулах знаком «¯» тот сомножитель, к которому оператор Ñ должен применяться. Тогда, как легко проверить, выражение для div (U А) можно записать так:

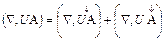Множители, на которые Ñ не действует, можно «высвободить» из-под оператора Ñ. Таким образом, получаем

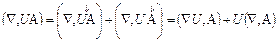
т. е. в обычных обозначениях

div (U А) = (А, grad U) + U div А.

2. Рассмотрим выражение

grad (UV),

которое в символической записи имеет вид

Ñ UV.

Руководствуясь сказанным выше, имеем

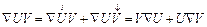т. е. в обычных обозначениях

grad (UV) = V grad U + U grad V.

Из рассмотренных примеров ясны правила, которые надо применять, пользуясь оператором Ñ: в выражениях, содержащих одну переменную, с ним можно поступать, как с обычным вектором, а к выражениям, содержащим произведения нескольких переменных, оператор Ñ применяется в соответствии с правилом дифференцирования произведения. Наконец, применение Ñ к сумме любых слагаемых всегда сводится к применению Ñ к каждому из слагаемых в отдельности.

Дадим в заключение сводку формул, связывающих операции взятия градиента, ротора и дивергенции с основными операциями векторной алгебры:

1. div (U А) = (А, grad U) + U div А;

2. grad (UV) = V grad U + U grad V; "

3. rot (U А) = U rot А + [grad U, А ];

4. div [ А, В ] = (В, rot А) - (А, rot B);

5. rot [ A, В ] = (В, Ñ) A - (A, Ñ) B + A div B – В div А;

6. grad (А, В) = (В, Ñ) А + (А, Ñ) В + [ В, rot А ] + [ А, rot В ];

в частности, положив в последней формуле А = В, получим

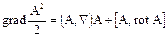Первые две из этих формул были получены раньше. Остальные могут быть получены аналогичным образом с применением оператора Ñ (и соблюдением указанных раньше правил действия с Ñ) и обычных формул векторной алгебры. В частности, для вычисления выражения rot [ А, В ], которое в символической форме пишется как

[Ñ, [ А, В ]],

следует применить известную формулу двойного векторного произведения:

[а, [b, с]] = b (а, с) - с (а, b).

Выражение вида (А, Ñ) В, встречающееся в последних двух формулах, означает векторную величину:

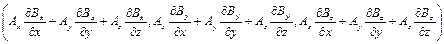которую можно рассматривать как результат применения «скалярной» операции

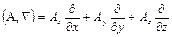
к каждой из компонент вектора В.

Лекция 9

1.6. Дифференциальные операции второго порядка.
Оператор Лапласа

1.6.1. Дифференциальные операции второго порядка.

На предыдущих лекциях мы ввели понятия градиента, дивергенции и ротора. В приложениях векторного анализа приходится встречаться не только с выполнением этих основных операций, но и с различными их комбинациями. Особенно часто встречаются так называемые Операции второго порядка, т. е. попарные комбинации трех указанных выше основных операций.

Комбинируя символы grad, rot, div попарно, мы можем составить из них девять пар. Однако не все эти пары имеют смысл; например, операция

rot div

(т. е. взятие ротора от дивергенции) не имеет смысла ни для скалярного поля, ни для векторного.

Все имеющиеся здесь возможности изображаются следующей таблицей, в которой заштрихованы клетки, отвечающие не имеющим смысла сочетаниям основных операций:

	Скалярное поле U	Векторное поле А
grad	div	rot
grad	ïïïïïïïïïïïïïï	grad div А	ïïïïïïïïïïïïïï
div	div grad U	ïïïïïïïïïïïïïï	div rot А
rot	rot grad U º 0	ïïïïïïïïïïïïïï	rot rot Аº 0

Мы видим, что применительно к скалярному полю имеют смысл две операции, а именно:

rot grad U,

div grad U.

Первое из этих выражений представляет собой ротор потенциального поля grad U, как мы видели, тождественно равно нулю.

Выражение div grad U, вообще говоря, не обязано быть нулем. Оно называется оператором Лапласа и обозначается D U. Воспользовавшись известными выражениями градиента и дивергенции в декартовых координатах, получаем:

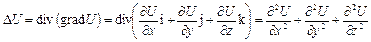Так как и дивергенция, и градиент не зависят, как мы знаем, от выбора координатной системы, то и D U зависит лишь от самого поля U, но не от системы координат. К оператору Лапласа мы еще вернемся ниже.

Оператор Лапласа D естественно рассматривать как скалярный квадрат вектора Ñ. Действительно,

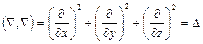т. е.

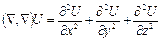
Иногда приходится оператор D применять не к скалярной величине, а к вектору. При этом если

А = A_х i+ A_y j + A_z k,

то под D А понимается вектор

D A_х i+ D A_y j + D A_z k.

Как мы увидим немного ниже, это выражение на самом деле зависит только от самого вектора А, но не от выбора системы координат.

Рассмотрим теперь операции второго порядка для векторного поля. Применительно к векторному полю имеют смысл три операции второго порядка, а именно:

grad div А,

rot rot А,

div rot А.

С выражением вида div rot А мы уже встречались при нахождении условий соленоидальности поля и выяснили, что всегда

div rot А º 0.

Напротив, выражения grad div А и rot rot А не обязаны обращаться в нуль. Они часто встречаются в различных вопросах механики и электродинамики.

Выведем формулу, связывающую эти величины. Рассмотрим для этого выражение

rot rot А,

которое в символической форме записывается так:

[Ñ, [Ñ, А ]].

Воспользовавшись снова формулой для двойного векторного произведения, получим, что

[Ñ, [Ñ, А ]] = Ñ (Ñ, A) - (Ñ,Ñ) A,

т. е.

rot rot А = grad div А - D А. (31)

Из этой формулы видно, в частности, что выражение D А, определенное ранее, действительно не зависит от выбора системы координат, поскольку величины rot rot А и grad div А с выбором системы координат не связаны.

Так как в выражении (31) участвует только одна переменная величина, то мы, оперируя с Ñ, мог ли воспользоваться обычными формулами векторной алгебры.

1.6.2. Уравнение теплопроводности.

В качестве применения введенных понятий рассмотрим вывод уравнения для поля температур внутри некоторого нагретого тела. Пусть U (х, у, z, t) - температура тела в точке (х, у, z) в момент t. Выделим в этом теле некоторый объем W, ограниченный замкнутой поверхностью S, и вычислим двумя способами изменение количества тепла внутри этого объема за малый промежуток времени dt. В каждом элементе объема температура за время dt меняется на величину

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

1 2

Подборка статей по вашей теме: