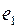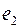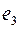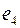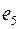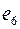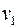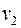Глава 2. ТЕОРИЯ ГРАФОВ
Определение. Графом  называется любая пара
называется любая пара  , где
, где 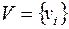 – множество элементов произвольной природы, называемых вершинами графа;
– множество элементов произвольной природы, называемых вершинами графа; 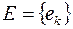 – семейство пар из
– семейство пар из 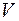 :
: 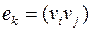 .
.
В множестве 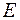 допускаются пары типа
допускаются пары типа 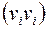 , а также повторяющиеся пары. Если пары
, а также повторяющиеся пары. Если пары 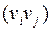 рассматриваются как неупорядоченные, то есть
рассматриваются как неупорядоченные, то есть 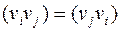 , то граф
, то граф 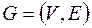 называется неориентированным и пары из множества
называется неориентированным и пары из множества 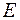 называются ребрами. Если пары считаются упорядоченными, то есть
называются ребрами. Если пары считаются упорядоченными, то есть 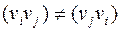 то граф называется ориентированным или орграфом и эти пары называются ориентированными ребрами или дугами.
то граф называется ориентированным или орграфом и эти пары называются ориентированными ребрами или дугами.
Пример 1. Рассмотрим граф 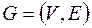 , где
, где 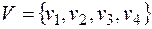 ,
, 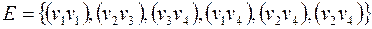 . Условно этот граф можно изобразить так, как показано на рис. 3.
. Условно этот граф можно изобразить так, как показано на рис. 3.
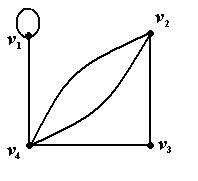
Рис. 3
Определение. Ребро вида 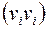 называется петлей при вершине
называется петлей при вершине 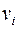 . Повторяющиеся в множестве
. Повторяющиеся в множестве 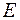 пары называются кратными ребрами.
пары называются кратными ребрами.
Иногда под термином «граф» подразумевается граф без кратных ребер и петель, тогда граф с кратными ребрами называется мультиграфом, а граф с кратными ребрами и петлями – псевдографом. Иногда граф без кратных ребер и петель называют простым графом.
Такое широкое определение графа допускает любую трактовку: множество предприятий с экономическими отношениями, множество людей с психологической совместимостью, система управления с подчинением, технические системы со связями, электрические цепи с источниками и потребителями, транспортные сети. Поэтому язык теории графов получил распространение в химии, физике, лингвистике, экономике, психологии и т.д.
Вершины 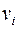 и
и 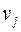 называются смежными, если либо пара
называются смежными, если либо пара 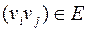 , либо
, либо 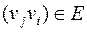 .
.
Вершина 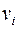 и ребро
и ребро 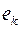 инцидентны, если
инцидентны, если 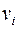 входит в пару
входит в пару 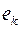 .
.
Ребра 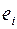 и
и 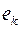 называются смежными, если они инцидентны одной и той же вершине.
называются смежными, если они инцидентны одной и той же вершине.
В неориентированном графе степенью вершины 
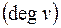 называется количество инцидентных ей ребер, причем петля учитывается дважды. Если
называется количество инцидентных ей ребер, причем петля учитывается дважды. Если 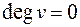 , то вершина
, то вершина  называется изолированной, если
называется изолированной, если 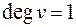 , то вершина
, то вершина  называется висячей.
называется висячей.
Так в приведенном примере 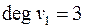 ,
, 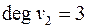 ,
, 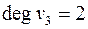 и
и 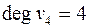 .
.
Мы будем рассматривать только конечные графы, то есть множества 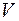 и
и 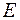 будут конечными, будем обозначать их мощности
будут конечными, будем обозначать их мощности 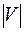 и
и 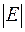 , соответственно.
, соответственно.
Лемма о рукопожатиях. Если 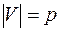 ,
, 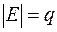 , то
, то  .
.
Доказательство очевидно, каждое ребро в этой сумме участвует ровно 2 раза, так как имеет 2 конца.
Из леммы вытекает, что число вершин с нечетной степенью четно.
Определение. Графы 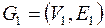 и
и 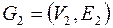 называются изоморфными, если существует биекция
называются изоморфными, если существует биекция 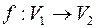 , причем если пара
, причем если пара 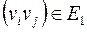 , то пара
, то пара 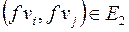 и наоборот.
и наоборот.
Чтобы установить изоморфизм графов достаточно одинаково занумеровать вершины множества 
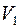 и соответствующие им при биекции
и соответствующие им при биекции 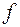 вершины множества
вершины множества 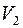 .
.
Пример 2. Графы 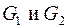 на рис. 4 – изоморфны.
на рис. 4 – изоморфны.
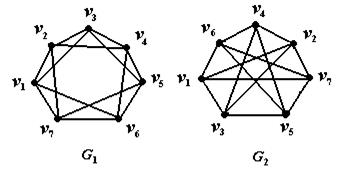
Рис. 4
Пример 3. Графы 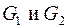 на рис. 5 изоморфны.
на рис. 5 изоморфны.
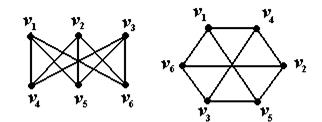
Рис. 5
Определение. Подграфом в графе 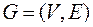 называют граф
называют граф  , в котором
, в котором  .
.
Графы можно задавать простым рисунком, или перечислением элементов множеств 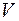 и
и 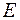 , или матрицами смежности, или матрицей инцидентности, или матрицей Кирхгофа.
, или матрицами смежности, или матрицей инцидентности, или матрицей Кирхгофа.
Матрица смежности вершин для неориентированного графа – это квадратная матрица размером 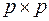 , где
, где 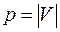 ; элемент матрицы
; элемент матрицы 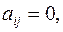 если пара
если пара 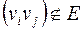 ,
, 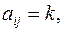 если вершины
если вершины 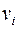 и
и 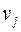 соединены
соединены  ребрам. Эта матрица позволяет задавать неориентированные графы с кратными ребрами и петлями.
ребрам. Эта матрица позволяет задавать неориентированные графы с кратными ребрами и петлями.
Матрица смежности вершин для графа, приведенного на рис. 3, имеет вид
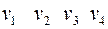
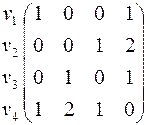 .
.
Аналогично можно задать матрицу смежности ребер для неориентированного графа, в ней элемент 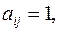 если ребра
если ребра 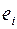 и
и 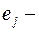 смежные. Она используется редко.
смежные. Она используется редко.
Матрица инцидентности употребляется часто и позволяет задавать ориентированные графы. Если граф  имеет вершины
имеет вершины 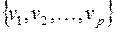 и ребра
и ребра 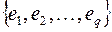 , то матрица инцидентности
, то матрица инцидентности 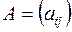 будет иметь размер
будет иметь размер 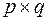 , и
, и 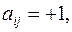 если ребро
если ребро 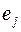 инцидентно вершине
инцидентно вершине 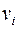 в остальных случаях
в остальных случаях 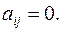 Если
Если 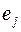 – петля при вершине
– петля при вершине 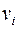 , тогда.
, тогда. 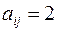 . Если граф ориентированный, то ориентация ребер указывается стрелкой и
. Если граф ориентированный, то ориентация ребер указывается стрелкой и 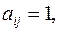 если ребро
если ребро 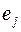 вошло в вершину
вошло в вершину 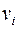 , и
, и 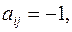 если
если 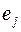 вышло из вершины
вышло из вершины 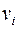 .
.
Обратимся к примеру 1, для того чтобы задать матрицу инцидентности, надо пронумеровать ребра графа. Получим соответствующую матрицу инцидентности
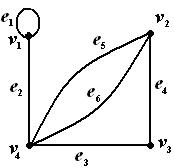 Рис. 6 Рис. 6
|
|
Изоморфные графы на рис. 5 имеют одну и ту же матрицу смежности
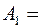
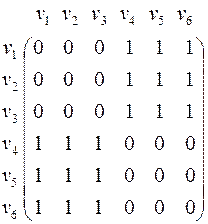 .
.
Для изоморфных графов, вершины которых занумерованы произвольным образом, матрицы смежности различны, но они получаются друг из друга одинаковыми перестановками строк и столбцов. То же самое верно для матриц инцидентности.
Пример 4. В примере 3 поменяем нумерацию вершин графа 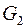 (рис. 7).
(рис. 7).
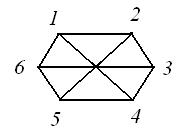
Рис. 7
Получим матрицу смежности:
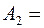
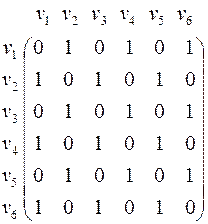 .
.
Матрицу 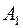 можно преобразовать в матрицу
можно преобразовать в матрицу 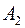 , поменяв местами вторую и четвертую строчки и столбцы, а затем в полученной матрице поменяв местами четвертую и пятую строки и столбцы.
, поменяв местами вторую и четвертую строчки и столбцы, а затем в полученной матрице поменяв местами четвертую и пятую строки и столбцы.
Матрица Кирхгофа – это квадратная матрица 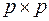 , где
, где 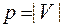 и элемент матрицы
и элемент матрицы 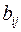 определяется следующим образом
определяется следующим образом 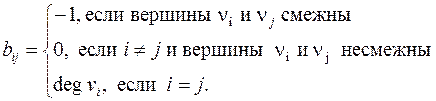
Сумма элементов в каждой строке и в каждом столбце матрицы равна 0.
 2015-05-20
2015-05-20 1244
1244