Вывод уравнения стоячей волны

Предположим, что две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания, причем обе волны характеризуются одинаковыми амплитудами и частотами. Кроме того, начало координат выберем в точке, в которой обе волны имеют одинаковую начальную фазу. Тогда соответственно уравнение волны, распространяющейся вдоль положительного направления оси х, и волны, распространяющейся ей навстречу, будут иметь вид

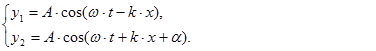
Сложив эти уравнения, получим уравнение стоячей волны:

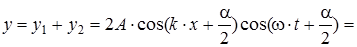
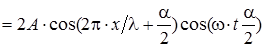
В каждой точке стоячей волны колебания происходят с той же частотой, что и у встречных волн. Амплитуда колебаний зависит от координаты x:

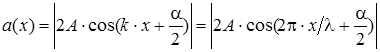
Для струны конечной длины с закрепленными концами амплитуда результирующего колебания на концах струны должна равняться нулю. Если начало струны находится в точке с координатой 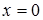, то амплитуда в этой точке будет равна нулю в том случае, когда 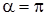. Выражение в том при этом будет иметь вид:

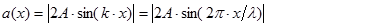
На конце струны, в точке с координатой 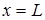, где 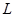- длина струны, амплитуда также должна ровняться нулю. Для этого должно выполняться условие:

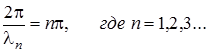
Из последнего выражения следует, что стоячие волны на струне могут существовать только на таких частотах 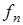, для которых длина волны

Частота колебаний связана с длиной волны соотношением 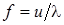, где u - фазовая скорость волны. Тогда частоты 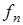могут быть определены по формуле:

В теории колебаний эти частоты называют гармониками (первая гармоника, вторая и т.д.) или собственными частотами колебания струны.

Зависимость амплитуды колебаний а от координаты x для различных номеров гармоник n может быть представлена выражениеми

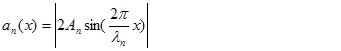
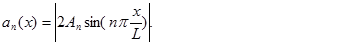
Тогда следует, что амплитуда равна нулю в тех точках струны, для которых 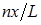принимает целочисленное или нулевое значение. Так для первой гармоники таких точек две, с координатам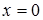и и 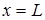, т.е. на концах струны. Для второй гармоники таких точек три: на концах струны и в точке 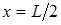, т.е. в средине струны. Для третьей гармоники – четыре точки: на концах струны и в точках с координатам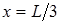и и .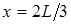

Точки, амплитуды колебаний в которых равны нулю, называют узлами стоячей волны. Расстояние между соседними узлами 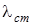называют длиной стоячей волны. Из выражения следует, что минимальное расстояние между узлами равно половине длины бегущей волны. Следовательно, .

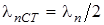На рисунке показана зависимость смещения точек струны y от координаты x на частоте второй гармоники для трех моментов времени: 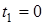(кривая 1); 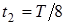, где T - период колебаний (кривая 2); 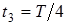(кривая 3).

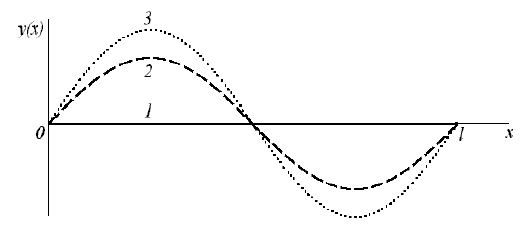
Видно, что точки струны между соседними узлами движутся в одинаковой фазе. Однако точки струны, расположенные по разные стороны узла на расстоянии, меньшем 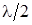движутся в противофазе.

В настоящей работе струна возбуждается силой, изменяющейся по гармоническому закону. Для этого используется металлическая струна, к концам которой подводится переменное электрическое напряжение от генератора звуковой частоты. Часть струны проходит через зазор между полюсами электромагнита, питаемого от источника постоянного тока. На эту часть струны действует сила Ампера в направлении, перпендикулярном длине струны и силовым линиям магнитного поля. Для эффективного возбуждения колебаний струны магнит должен быть расположен так, чтобы между полюсами магнита находилась пучность стоячей волны.

В отличие от бегущей волны, в стоячей волне не происходит переноса энергии вдоль струны. Поэтому, в случае отсутствия потерь энергии, даже при кратковременном, импульсном возбуждении струна должна колебаться бесконечно долго. Однако реально всегда существуют потери энергии (например, на излучение звука) и колебания являются затухающими. При возбуждении струны силой, изменяющейся по гармоническому закону (от генератора электрических колебаний), колебания являются вынужденными. В установившемся режиме они происходят с частотой вынуждающей силы, и амплитуда колебаний со временем не меняется. Потери энергии компенсируются энергией, поступающей от генератора.