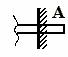| Наименование связей и их обозначение на схемах | Реакции связей | ||||
гладкая поверхность (точка А) и уступ (точка В)

| Реакция 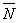 направлена к телу. Реакция направлена к телу. Реакция 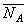 гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел. Реакция гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел. Реакция 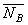 уступа направлена по нормали к поверхности опирающегося тела. уступа направлена по нормали к поверхности опирающегося тела.
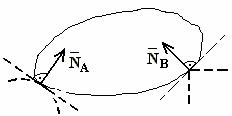
| ||||
Нить
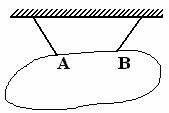
| Реакция 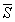 направлена вдоль нити от тела (нить работает только на растяжение) направлена вдоль нити от тела (нить работает только на растяжение)
| ||||
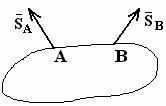
Невесомый стержень с шарнирами на концах
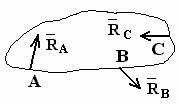
| Реакция 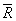 направлена вдоль стержня, стержень работает либо на растяжение, либо на сжатие. направлена вдоль стержня, стержень работает либо на растяжение, либо на сжатие.
| ||||
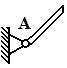
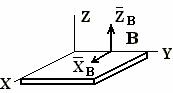
4. цилиндрический шарнир (подшипник)
А – ось подшипника перпендикулярна чертежу
 В – ось подшипника совпадает с осью Y
В – ось подшипника совпадает с осью Y
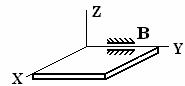
| Составляющие реакции лежат в плоскости, перпендикулярной оси шарнира.
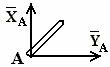
| ||||
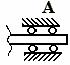
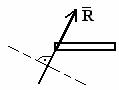
5. подвижная шарнирная опора (на катках)
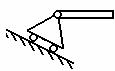
| Реакция направлена перпендикулярно опорной плоскости
| ||||
6. Заделка
| Реакции при действии на тело плоской системы сил
|
Порядок (план) решения задач.
|
|
|
Приступая к решению задания, необходимо разобраться в условии задачи и рисунке, а затем:
1. Составить расчетную схему, которая включает:
- объект равновесия,
- активные (заданные) силы,
- силы реакции, заменяющие действия отброшенных связей.
2. Определить вид полученной системы сил и выбрать, соответствующие ей, уравнения равновесия;
3. Выяснить, является ли задача статически определимой;
4. Составить уравнения равновесия и определить из них силы реакции;
5. Сделать проверку полученных результатов.
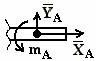
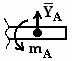
При замене связей (опор) силами реакций помнить:
- если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению;
- если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают ее составляющими, показывая их параллельно выбранным координатным осям 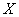 и
и 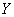 .
.
Решение уравнений равновесия будет тем проще, чем меньшее число неизвестных будет входить в каждое из них. Поэтому, при составлении уравнений равновесия следует:
1) координатные оси 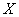 и
и 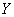 располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
2) за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных сил реакций, тогда моменты этих сил не войдут в уравнение моментов.
Если сила 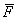 в плоскости
в плоскости 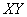 имеет две составляющие ее силы
имеет две составляющие ее силы 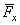 и
и 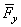 , то при вычислении момента силы
, то при вычислении момента силы 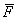 вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
|
|
|
Если к телу в числе других сил приложена пара сил, то ее действие учитывается только в уравнении моментов сил, куда вносится момент этой пары, с соответствующим, знаком.
Система сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.
Согласно аксиоме статики, равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис.9).
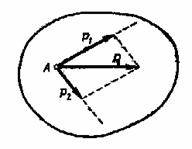
Рис.9
Из треугольника 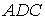 находим модуль равнодействующей по формуле
находим модуль равнодействующей по формуле
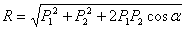 ,
,
где 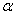 -угол между векторами
-угол между векторами 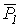 и
и 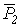 .
.
Применяя последовательно правило параллелограмма, можно найти равнодействующую скольких угодно сходящихся сил. Найдем сначала равнодействующую трех сил 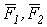 и
и 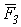 , приложенных в одной точке и не лежащих в одной плоскости (рис.10).
, приложенных в одной точке и не лежащих в одной плоскости (рис.10).
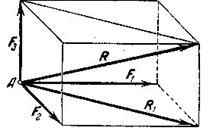
Рис.10
Сложив по правилу параллелограмма силы 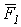 и
и 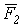 , получим их равнодействующую
, получим их равнодействующую 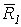 , а сложив затем
, а сложив затем 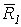 и
и 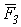 , найдем равнодействующую
, найдем равнодействующую 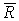 трех данных сил
трех данных сил 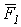 ,
, 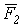 и
и 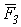 . Таким образом, равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (правило параллелепипеда). Заметим, что при нахождении равнодействующей двух сил нет надобности строить весь параллелограмм. Для этого из конца вектора первой силы
. Таким образом, равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (правило параллелепипеда). Заметим, что при нахождении равнодействующей двух сил нет надобности строить весь параллелограмм. Для этого из конца вектора первой силы  (рис.11) проводим вектор второй силы
(рис.11) проводим вектор второй силы 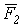 . Вектор, соединяющий начальную и конечную точки полученной ломаной линии будет представлять собой по модулю и направлению равнодействующую
. Вектор, соединяющий начальную и конечную точки полученной ломаной линии будет представлять собой по модулю и направлению равнодействующую 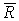 двух данных сил
двух данных сил 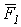 и
и 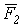 (правило треугольника).
(правило треугольника).
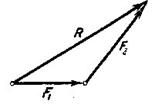
Рис.11
Как известно, в статике сила является скользящим вектором. Поэтому, точки приложения сходящихся сил можно перенести по линиям их действия в точку пересечения этих линий, а следовательно, систему сходящихся сил всегда можно заменить системой сил, приложенных в одной точке.
Пусть теперь нужно сложить несколько сил, например, четыре силы 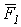 ,
, 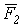 ,
, 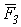 и
и 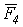 , приложенных в точке
, приложенных в точке 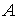 (рис.12). Применяя последовательно правило треугольника, получим ломаную линию
(рис.12). Применяя последовательно правило треугольника, получим ломаную линию 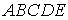 . Вектор
. Вектор 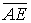 , соединяющий начальную и конечную точки ломаной линии, изображает искомую равнодействующую
, соединяющий начальную и конечную точки ломаной линии, изображает искомую равнодействующую 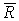 четырех сил
четырех сил 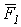 ,
, 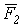 ,
, 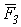 и
и 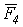 .
.
Рис.12
Таким образом, равнодействующая сходящихся сил изображается замыкающей стороной многоугольника сил, приложена в точке пересечения линий действия сил и равна их геометрической сумме
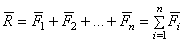 . (6)
. (6)
Спроектировав равенство (6) на координатные оси, и учитывая, что проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций векторов на ту же ось, получим
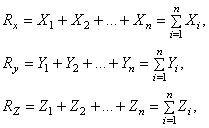 (7)
(7)
где 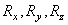 и
и 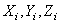 - проекции соответственно равнодействующей и сил системы на координатные оси.
- проекции соответственно равнодействующей и сил системы на координатные оси.
Модуль равнодействующей определяется по формуле
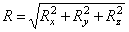 . (8)
. (8)
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил равнялась нулю.
Так как равнодействующая 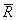 изображается вектором, замыкающим силовой многоугольник, то для того чтобы равнодействующая равнялась нулю, силовой многоугольник должен быть замкнутым, то есть конец вектора, изображающего последнюю силу, должен совпадать с началом вектора, изображающего первую силу.
изображается вектором, замыкающим силовой многоугольник, то для того чтобы равнодействующая равнялась нулю, силовой многоугольник должен быть замкнутым, то есть конец вектора, изображающего последнюю силу, должен совпадать с началом вектора, изображающего первую силу.
Таково условие равновесия системы сходящихся сил в геометрической форме. Выразим теперь то же условие аналитически.
Из (8) следует, что при равновесии должно иметь место равенство
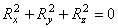 .
.
Так как все слагаемые в левой части не могут быть отрицательными, то это равенство справедливо только в случае, если 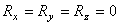 . С учетом (7), окончательно получим
. С учетом (7), окончательно получим
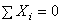 ,
, 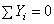 ,
, 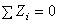 . (9)
. (9)
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех этих сил на каждую из трех координатных осей равнялась нулю.
|
|
|
Понятно, что в случае плоской системы сходящихся сил для равновесия должны быть выполнены только первые два из условий (9).
При решении задач статики иногда удобно пользоваться теоремой о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
В большинстве случаев в задачах статики по заданным (известным) силам, приложенным к данному несвободному твердому телу, требуется определить неизвестные реакции связей, предполагая, что тело находится в покое и все приложенные к нему силы уравновешиваются. При аналитическом решении задачи эти силы находятся из уравнений (9), в левые части которых войдут, кроме заданных известных сил, и неизвестные реакции связей.
Рассмотрим примеры.
Пример 1. Шар веса 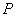 опирается в точке
опирается в точке 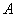 на наклонную плоскость, образующую с вертикалью угол
на наклонную плоскость, образующую с вертикалью угол 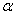 , и привязан к стене веревкой, которая образует с вертикалью угол
, и привязан к стене веревкой, которая образует с вертикалью угол 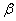 (рис.13а). Определить реакцию плоскости в точке
(рис.13а). Определить реакцию плоскости в точке 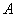 и натяжение веревки.
и натяжение веревки.
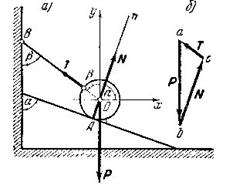
Рис.13
Решение: Обозначим искомую реакцию плоскости, направленную по нормали 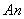 к этой плоскости, через
к этой плоскости, через 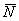 , а натяжение веревки – через
, а натяжение веревки – через 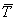 . Линия действия всех трех сил
. Линия действия всех трех сил 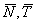 и
и 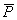 пересекаются в центре шара
пересекаются в центре шара 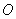 . Примем вертикаль и горизонталь в точке
. Примем вертикаль и горизонталь в точке 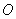 за координатные оси и найдем проекции сил
за координатные оси и найдем проекции сил 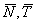 и
и 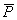 на эти оси:
на эти оси:
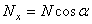 ,
, 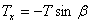 ,
, 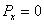 ,
,
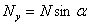 ,
, 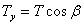 ,
, 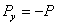 .
.
Так как данная система сходящихся сил является плоской, то условия равновесия (4) имеют вид
1) 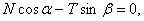
2) 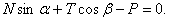
Умножив первое уравнение на 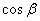 , а второе на
, а второе на 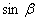 и сложив их, получим
и сложив их, получим
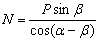 .
.
Затем из первого уравнения находим
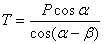 .
.
В случае, когда веревка, удерживающая шар, параллельна наклонной плоскости 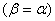 , получим
, получим 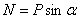 ,
, 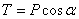 .
.
Для решения этой же задачи графическим способом, необходимо построить замкнутый силовой многоугольник. Построение силового многоугольника всегда нужно начинать с известных, заданных сил. Из произвольной точки  (рис.13б) проведем вектор
(рис.13б) проведем вектор 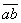 , параллельный данной силе
, параллельный данной силе 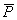 , длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки
, длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки 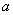 и
и 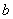 проводим прямые, параллельные линиям действия искомых сил
проводим прямые, параллельные линиям действия искомых сил 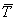 и
и 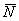 , которые пересекутся в точке
, которые пересекутся в точке 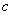 . Векторы
. Векторы 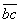 и
и 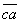 определяют искомые силы
определяют искомые силы 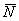 и
и 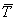 .Чтобы найти направление искомых сил на силовом треугольнике, нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы
.Чтобы найти направление искомых сил на силовом треугольнике, нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы 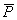 . Измерив длину сторон
. Измерив длину сторон 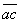 и
и 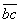 и зная масштаб, в котором построена сила
и зная масштаб, в котором построена сила 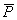 , найдем численные значения сил
, найдем численные значения сил 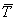 и
и 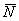 .
.
|
|
|
Пример 2. Определить реакции стержней, удерживающих грузы F1=70 кН и F2=100 кН (рис 14,а). Массой стержней пренебречь.
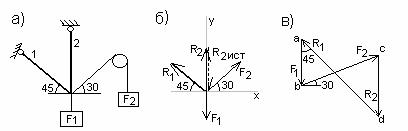
Рис.14
Указание. В данной задаче рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач такого типа универсальным является аналитический метод решения.
Последовательность решения задачи:
1. выбрать тело (точку), равновесие которого следует рассматривать;
2. освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принять считать предположительно стержни растянутыми;
3. выбрать систему координат, совместив ее начало с точкой В, и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости 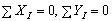 ;
;
4. определить реакции стержней из решения указанной системы уравнений;
5. проверить правильность полученных результатов по уравнению, которое не использовалось при решении задачи, либо решить задачу графически.
 2015-05-12
2015-05-12 3764
3764