На практике приходится иметь дело с воздействиями более сложного типа, чем гармонический сигнал. Чтобы получить представление о принципах расчета цепей при произвольных периодических воздействиях, рассмотрим линейный двухполюсник, к которому прикладывается n-гармонических напряжений с различными амплитудами и кратными частотами колебаний, т.е. 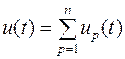 . Исследуемая цепь является линейной и к ней применим принцип суперпозиции. Согласно этому принципу ток, текущий в двухполюснике, равен сумме токов, возбуждаемых гармоническими напряжениями, т.е.
. Исследуемая цепь является линейной и к ней применим принцип суперпозиции. Согласно этому принципу ток, текущий в двухполюснике, равен сумме токов, возбуждаемых гармоническими напряжениями, т.е. 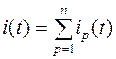 . Поэтому расчет тока в цепи сводится к вычислению откликов на отдельные гармонические воздействия.
. Поэтому расчет тока в цепи сводится к вычислению откликов на отдельные гармонические воздействия.
Если функция S(t)= S(t+nT), то ее можно разложить в ряд Фурье
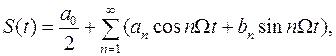 (1.15)
(1.15)
а коэффициенты Фурье
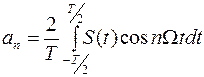 , (1.16)
, (1.16)
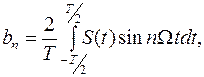 (1.17)
(1.17)
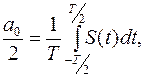 (1.13)
(1.13)
где Ω=2π/T.
Разложение (1.10) можно представить в тригонометрической форме:
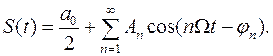 (1.18)
(1.18)
Здесь
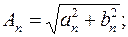 (1.19)
(1.19)
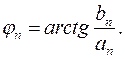 (1.20)
(1.20)
Совокупность гармонических составляющих, на которые раскладывается функция S(t), называется спектром. Спектр периодической функции сложной формы, как вытекает из разложения (1.18) состоит из постоянной составляющей и множества гармонических составляющих, частоты которых образует дискретный ряд значений nΩ (n=1,2,3…), кратных основной частоте Ω. Амплитуды гармонических составляющих (или сокращенно гармоник) равны Аn, а начальные фазы φn. Такой спектр называется дискретным или линейчатым.
Заметим, что постоянную составляющую в разложении (1.18) можно рассматривать как гармонику с нулевой частотой колебания и амплитудой А0=а0/2.
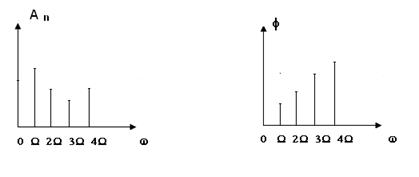
В общем случае гармонические колебания, входящие в состав спектра, будут иметь различные амплитуды и фазы. Чтобы получить наглядное представление о спектре, целесообразно воспользоваться графиками – так называемыми спектральными диаграммами. Различают два типа диаграмм: амплитудные и фазовые, которые представлены на рис. 1.9 (амплитудная - а, фазовая -б).
а) б)
Рис.1.9
Ряды Фурье могут быть записаны в комплексном виде. Известно, что
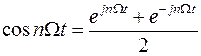 и
и 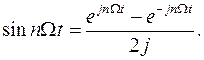
Подставляя эти выражения в разложение (1.15), после несложных преобразований получим
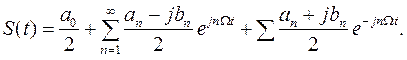 (1.21)
(1.21)
Воспользуемся далее обозначениями:

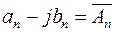 и
и 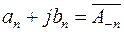 .
.
Тогда вместо 1.21 будем иметь
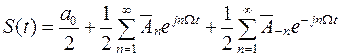 .
.
Полагая 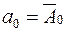 и учитывая, что
и учитывая, что
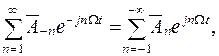
приведем разложение S(t) к окончательному виду:
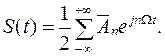 (1.22)
(1.22)
Равенство 1.18 есть комплексный ряд Фурье функции S(t).
Комплексный коэффициент Фурье 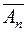 с учетом выражений (1.16) и (1.17) определяется так:
с учетом выражений (1.16) и (1.17) определяется так:
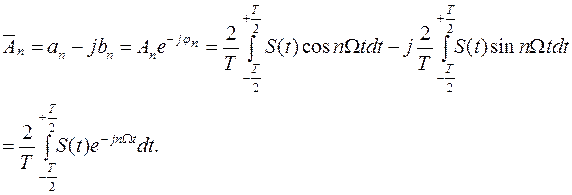 (1.23)
(1.23)
В разложении 1.22 суммирование членов происходит как по положительным, так и по отрицательным n. Это означает, что комплексный ряд Фурье содержит гармоники не только с положительными, но и отрицательными частотами. Совершенно ясно, что последние частоты никакого физического смысла не имеют. Они появляются только как следствие формального представления тригонометрических функций с мнимым аргументом.
Очевидно, гармонические колебания с отрицательной частотой по аналогии с колебаниями, имеющими положительную частоту, можно представить в виде вектора, который вращается по плоскости с постоянной угловой частотой по часовой стрелке.
Найдем расстояния между соседними линиями спектра:
(n+1)Ω –nΩ = (n+1)2π/T -n 2π/T=2π/T.
При увеличении T это расстояние уменьшается, и спектр становится более плотным. От величины T зависят также амплитуды гармонических составляющих спектра. Зависимость комплексных амплитуд гармонических составляющих от частоты (если ω рассматривать как непрерывную переменную) определяется функцией
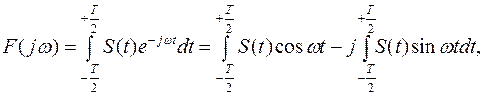 (1.24) которая не содержит T и носит название спектральной функции.
(1.24) которая не содержит T и носит название спектральной функции.
Из выражений (1.23) и (1.24) вытекает, что
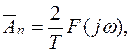 если
если 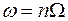 . (1.24а)
. (1.24а)
 2015-05-13
2015-05-13 795
795








