Рассмотрим множество квадратных матриц
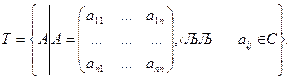
Введем на множестве Т операции сложения и умножения следующим образом
"A,BÎT (A+B)=С, где 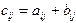 , i=1,2,...,n, j=1,2,...,n.
, i=1,2,...,n, j=1,2,...,n.
"A,BÎT (A´B)=С, где 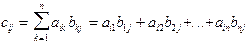 i=1,2,...,n, j=1,2,...,n, то есть элемент, стоящий на пересечении i строки и j столбца матрицы С, получен как сумма произведений элементов i строки матрицы А на соответствующие элементы j столбца матрицы В.
i=1,2,...,n, j=1,2,...,n, то есть элемент, стоящий на пересечении i строки и j столбца матрицы С, получен как сумма произведений элементов i строки матрицы А на соответствующие элементы j столбца матрицы В.
Пример. Найти сумму и произведение матриц
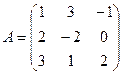 и
и 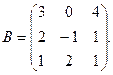
По определению суммы матриц, имеем
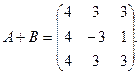
По определению произведения матриц, имеем
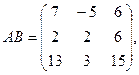
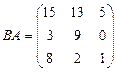
Из приведенного примера видно, что умножение матриц не коммутативно.
Теорема. Алгебра матриц Т=(Т, +, ´) образует кольцо.
Доказательство
Самостоятельно проверить выполнимость аксиом замкнутости относительно сложения (А0) и умножения (М0), ассоциативности (А1) и коммутативности (А1¢) сложения. Проверим выполнимость аксиомы А2. Покажем, что уравнение А+Х=В однозначно разрешимо в алгебре Т. Для этого достаточно рассмотреть уравнение для произвольных элементов матриц 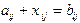 , где
, где 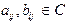 . Но в поле С такое уравнение всегда однозначно разрешимо, следовательно, каждый элемент матрицы Х определяется однозначно, то есть аксиома А2 выполняется, и алгебра Т относительно операции сложения образует абелеву группу. Проверим выполнимость аксиомы ассоциативности умножения (М1)
. Но в поле С такое уравнение всегда однозначно разрешимо, следовательно, каждый элемент матрицы Х определяется однозначно, то есть аксиома А2 выполняется, и алгебра Т относительно операции сложения образует абелеву группу. Проверим выполнимость аксиомы ассоциативности умножения (М1)
"A, B, СÎT(A(BС)=(AB)С).
Обозначим AB=L, (AB)С=M, BС=U, A(BС)=V и покажем, что для произвольных элементов имеет место mij=vij. Действительно,
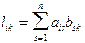 ,
,  ,
, 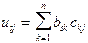
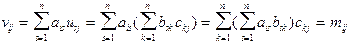 , тогда и М=V.
, тогда и М=V.
Аналогично проверить, что выполняется аксиома дистрибутивности. Легко видеть, что алгебра Т=(Т,+,´) образует некоммутативное кольцо с единицей. Роль единицы играет матрица
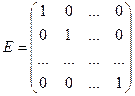 .
.
Мы доказали, что алгебра матриц не является полем. Возникает вопрос: существуют ли обратимые матрицы и если да, то какие? Попробуем найти ответ на этот вопрос.
Теорема (об определителе произведения матриц). Определитель произведения матриц равен произведению определителей перемножаемых матриц. ½AB½=½A½½B½.
Доказательство
Для доказательства рассмотрим определитель
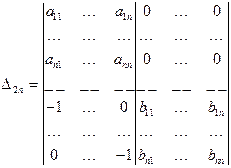
и подсчитаем его двумя различными способами.
1. Разложив определитель по первым n строкам по теореме Лапласа, получим D2n=½A½½B½+0, так как в любом из оставшихся миноров один столбец будет целиком состоять из нулей.
2. Преобразуем определитель. К каждому j столбцу от n+1 до 2n прибавим первый, умноженный на b1j , затем второй, умноженный на b2j, и так далее, и, наконец, n-ый столбец, умноженный на bnj. Получим в i строке в n+1 столбце элемент сi1=ai1b11+ai2b21+ai3b31+...+ainbn1. То есть получим определитель
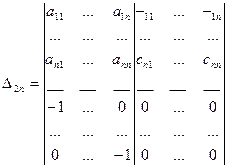 ,
,
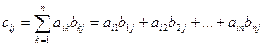 где i=1,2,...,n, j=1,2,...,n.
где i=1,2,...,n, j=1,2,...,n.
Теперь применив теорему Лапласа к последним n столбцам, получим
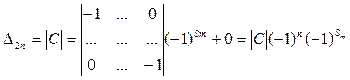 ,
,
где
Sm=n+1+n+2+...+2n+1+2+...+n=1+2+...+n+(n+1)+...+2n 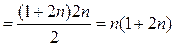
D2n=½C½ 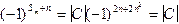 ,
,
где С=АВ, таким образом, ½AB½=½A½½B½.
Определение. Квадратная матрица, определитель которой отличен от 0, называется невырожденной. Квадратная матрица, определитель которой равен 0, называется вырожденной.
Следствие 1. Вырожденная матрица не обратима.
(Доказательство - самостоятельно. )
Следствие 2. Произведение невырожденных матриц есть невырожденная матрица.
(Доказательство - самостоятельно. )
Следствие 3. Множество невырожденных квадратных матриц порядка n образуют группу относительно операции умножения.
Доказательство
Так как множество невырожденных квадратных матриц порядка n
1) является подмножеством кольца квадратных матриц Т,
2) замкнуто относительно операции умножения,
то относительно операции умножения это множество образует полугруппу. Очевидно, что единичная матрица является невырожденной ½E½=1¹0, следовательно, единичная матрица принадлежит множеству невырожденных квадратных матриц. Пусть А - произвольная невырожденная квадратная матрица порядка n. Найдем матрицу, обратную для А. Пусть
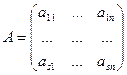 , ½А½¹0.
, ½А½¹0.
Рассмотрим матрицу
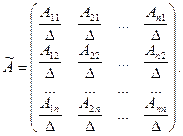 (*)
(*)
Докажем, что 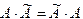 =Е Рассмотрим произвольный элемент матрицы
=Е Рассмотрим произвольный элемент матрицы
С= 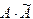
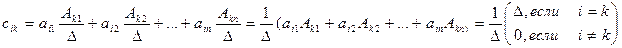
тогда
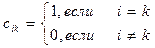 ,
,
таким образом, С=Е.
Аналогично доказывается, что 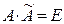 . Следовательно, для любой невырожденной матрицы существует обратная, вычисляемая по формуле (*), где Аij - алгебраическое дополнение к элементу aij.
. Следовательно, для любой невырожденной матрицы существует обратная, вычисляемая по формуле (*), где Аij - алгебраическое дополнение к элементу aij.
Из приведенного доказательства получаем алгоритм вычисления обратной матрицы:
1) вычислить определитель матрицы ½A½=D;
2) найти алгебраические дополнения ко всем элементам матрицы;
3) все элементы матрицы заменить их алгебраическими дополнениями, (получится матрица, которая называется присоединенной к матрице А);
4) транспонировать полученную матрицу;
5) разделить все элементы матрицы на D, получим матрицу А-1.
Пример. Вычислить матрицу, обратную матрице
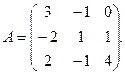
Найдем определитель матрицы А
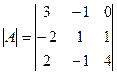 =12+0-2-0+3-8=5
=12+0-2-0+3-8=5
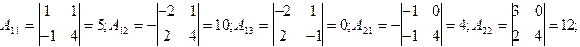

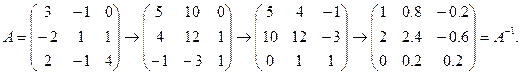
 2015-05-13
2015-05-13 8552
8552
