Случайные величины. Отличие дискретной и непрерывной случайных величин

Отличие дискретной и непрерывной случайных величин

Введем обозначения:

СВ – случайная величина,

ДСВ – дискретная случайная величина,

НСВ – непрерывная случайная величина.

С лучайная величина, это переменная величина, которая в результате испытания, принимает из множества возможных значений какое-то наперед неизвестное возможное значение, зависящее от таких причин, которые учесть и предсказать до опыта не удается.

Обозначают случайные величины заглавными (большими) буквами: X, Y, Z,…, а их значения обозначают прописными буквами х1, х2, …, y1, y2, ….

Дискретной называется случайная величина, которая может принимать только отдельные изолированные возможные значения x _i с определенными вероятностями p _i.

Число возможных значений ДСВ может быть конечным, или бесконечным счетным, то есть каждое значение может быть пронумеровано.

Непрерывной называется случайная величина, которая может принимать все (любые) значения из некоторого конечного или бесконечного промежутка (а,в) на числовой оси.

Количество значений НСВ бесконечно.

Примеры ДСВ и НСВ (устно).

Закон распределения вероятностей ДСВ.

Вариант (варианта). Многоугольник распределения вероятностей.

Свойство суммы вероятностей всех значений ДСВ.

Соответствие между возможными значениями х_i случайной величины X и вероятностями их появления p_i называется законом распределения вероят- ностей ДСВ (распределением вероятностей).

Закон распределения вероятностей можно задавать такими же способами, какими способами задают функции:

1. табличным;

2. графическим;

3. аналитическим;

4. другими (см. способы задания функции).

Покажем способы задания закона распределения вероятностей.

1. Табличный, то есть с помощью таблицы

X	х1	х2	…	хn
p	р1	р2	…	рn

Где х₁ – вариант(варианта),

р₁ – вероятность события, заключающегося в том, что случайная величина Х примет значение Х= х₁.

2. Графический, то есть с помощью графика, на котором указано соответствие: каждому значению х_к случайной величины соответствует свое значение вероятности р_к.

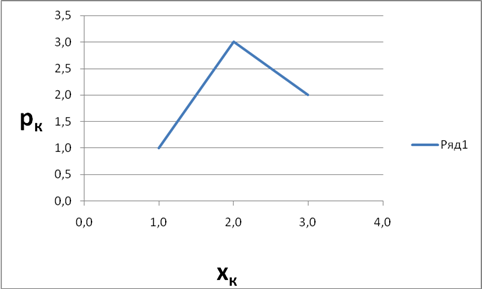
3. Аналитический, то есть с помощью формулы (аналитической записи), позволяющей для каждого значения х_к вычислить соответствующее ему значение р_к.

Например, по формуле Бернулли

р_к=р(Х=х_к=к)= .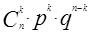

Медиана

Медиана это некоторое значение случайной величины Х такое, что выполняется условие

Р(Х<М е)=0,5= Р(Х>М е),

то есть вероятность того, что случайная величина Х окажется меньше, чем медиана М е, равна вероятности того, что случайная величина окажется больше, чем М е, и обе эти вероятностиравны 0,5.

Мода

Значение Х=х_к случайной величины такое, при котором значение вероятности Р(х_к) принимает наибольшее значение, называется модой.

Пример. Закон распределения вероятностей задан таблично

Х
р	0,01	0,4	0,09	0,45	0,05

Найти медиану и моду.

Решение. 1. Так как 0,01+0,4+0,09= 0,5=0,45+0,05, то любое значение случайной величины равное числу, принадлежащему интервалу (7,10), (например, Х=8.5), является медианой.

Примечание: Х=7 и Х=10 не являются медианами.

2. Так как р_max=0.45, то мода равна Мо=10.

Перечень числовых характеристик распределений вероятностей

1. М(Х) – математическое ожидание случайной величины,

2. D(X) – дисперсия случайной величины,

3. σ(Х) – среднее квадратическое отклонение.

Математическое ожидание

Математическим ожиданием ДСВ Х называется число, равное сумме произведений всех возможных значений х_i случайной величины на соответствующие вероятности р_i их появления.

Вероятностный смысл математического ожидания в том, что среднее арифметическое от наблюдаемых значений х _i случайной величины Х при неограниченном возрастании числа испытаний стремится к её математическому ожиданию М(Х).