Звено 2-го порядка

Это звено, дифференциальное уравнение которого

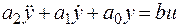, (3.39)

принято записывать в стандартном виде:

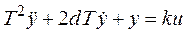, (3.40)

где 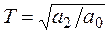- постоянная времени звена; d - коэффициент демпфирования, который определяет склонность звена к колебаниям, 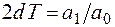; 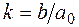- коэффициент усиления.

Передаточную функцию получим на основе символической записи дифференциального уравнения,

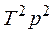y + 2d 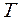py + y = ku,

в виде:

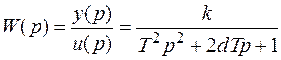. (3.41)

Определим модальные характеристики по характеристическому уравнению

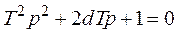. (3.42)

Оно имеет два корня, которые в зависимости от коэффициента демпфирования могут быть вещественными и комплексно - сопряженными, что приводит к различным переходным процессам в звене.

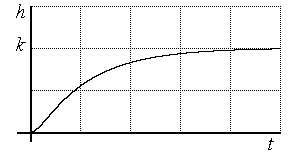
1). Если 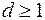, то корни уравнения (3.42) вещественные. Обозначим их через 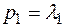, 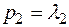и получим переходную функцию в виде:

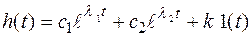. (3.43)

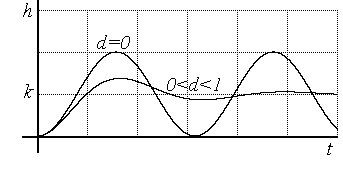
Рис. 3.21. Переходная характеристика звена 2-го порядка при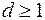

2). Если 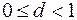, то корни уравнения (3.42) будут комплексно - сопряженными, то есть 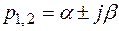(а при d = 0 вырождаются в ).

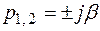Рис. 3.22. Переходная характеристика звена при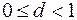

В этом случае звено второго порядка называют колебательным. Его переходная характеристика следующая:

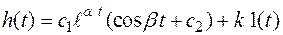. (3.44)

Колебательность переходного процесса зависит от коэффициента демпфирования d: колебания будут тем больше, чем меньше d. При d =0 имеют место незатухающие колебания.

Определим частотные характеристики звена, заменив p на j 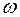в передаточной функции (3.41).

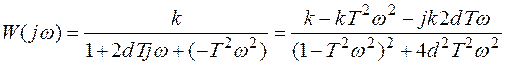. (3.45)

Отсюда получим выражения для ВЧХ и МЧХ в виде:

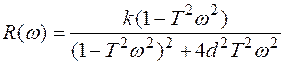, (3.46)

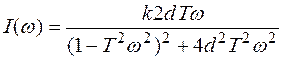. (3.47)

При построении АФХ на комплексной плоскости необходимо рассматривать характерные точки:

.

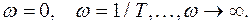
Вид АФХ существенно зависит от k и d. При d=0 АФХ располагается на вещественной оси.

Рис. 3.23. АФХ звена второго порядка

На основе выражения

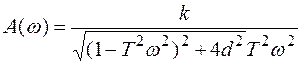(3.48)

строится точная ЛАЧХ колебательного звена (при 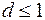). Его асимптотическую ЛАЧХ также можно построить, если рассматривать отдельно области высоких и низких частот и для каждой определить свою асимптоту:

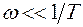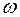ОНЧ: , L()=L₁(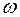)=20lgk. (3.49)

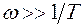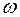ОВЧ: , L()=L₂(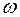)=20lgk-40lg(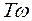). (3.50)

Частота 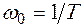называется собственной частотой колебательного звена. Причем на этой частоте для асимптотической ЛАЧХ справедливо соотношение: .

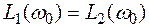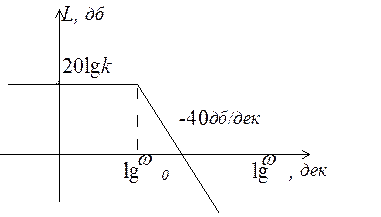
Наибольшее отличие асимптотической ЛАЧХ от действительной наблюдается на собственной частоте 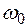и зависит от коэффициента демпфирования. При 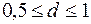с достаточной точностью можно применять асимптотическую ЛАЧХ звена.

Рис. 3.24. Асимптотическая ЛАЧХ колебательного звена

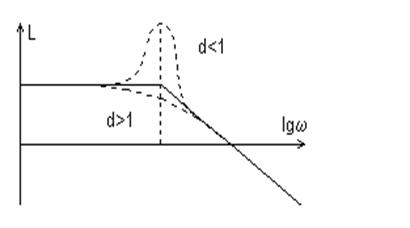
Если d < 0,5, то следует строить точную ЛАЧХ.

При d > 1 корни характеристического уравнения (3.42) будут вещественными, и передаточную функцию звена второго порядка (3.41) можно представить в виде произведения двух передаточных функций апериодических звеньев:

Рис. 3.25. Влияние d на ЛАЧХ звена

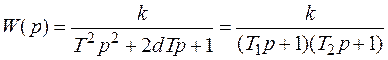, (3.51)

где 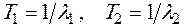- постоянные времени апериодических звеньев. В этом случае асимптотическая ЛАЧХ звена второго порядка имеет два излома на частотах 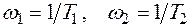. Она может быть получена суммированием асимптотических ЛАЧХ двух апериодических звеньев.