Закон нормального распределения должен быть изучен наиболее основательно, т.к. он часть используется в теории и практике.
Непрерывная случайная величина 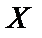 распределена по нормальному закону, если ее плотность распределения вероятностей выражается формулой:
распределена по нормальному закону, если ее плотность распределения вероятностей выражается формулой:
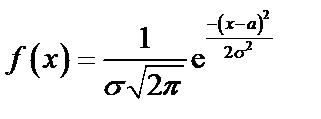 (67)
(67)
Параметры 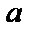 и
и 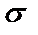 имеют следующий вероятностный смысл:
имеют следующий вероятностный смысл:
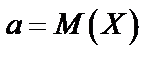 ;
; 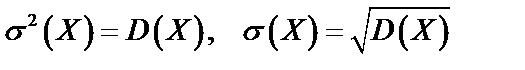
Если функция Лапласа задается формулой 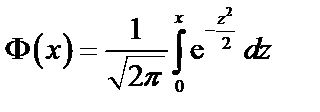 , то для нормально распределенной случайной величины
, то для нормально распределенной случайной величины 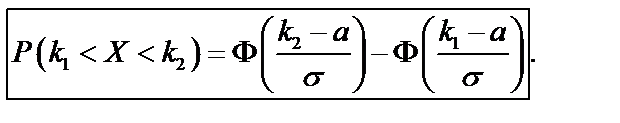 (68)
(68)
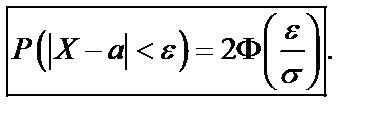 (69)
(69)
Если функция Лапласа задается формулой 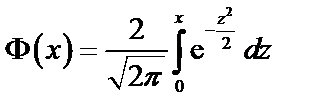 , то
, то 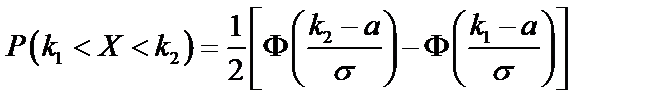 и
и 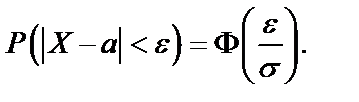
Глава 7. Пример решения варианта контрольной работы.
Задача 1. Вычислить 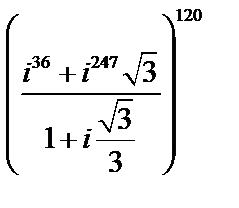 .
.
Решение: Преобразуем числитель дроби по формуле (6):
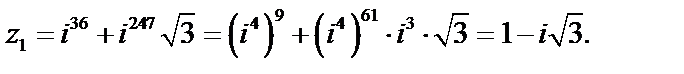
Числа 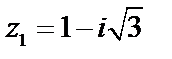 и
и 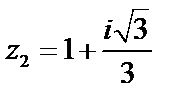 представим в тригонометрической форме:
представим в тригонометрической форме:
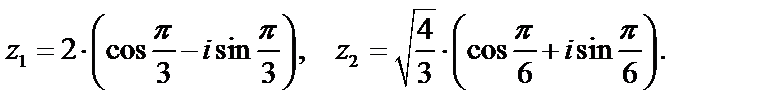
Тогда по формуле (4):
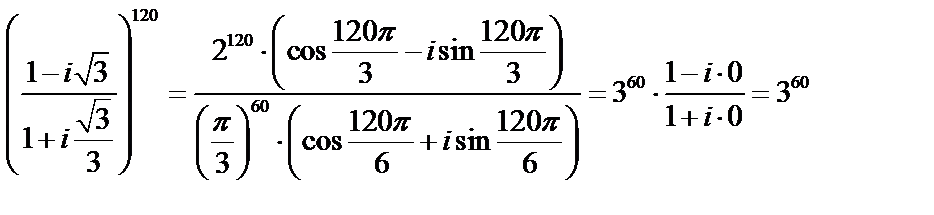 .
.
Ответ: 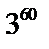 .
.
Задача 2. Решить уравнение 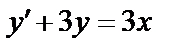 .
.
Решение: Пусть 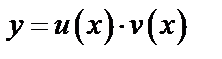 , тогда
, тогда 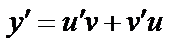 .
.
Подставив в уравнение, получим 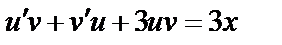
или
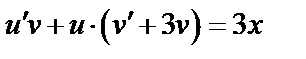 (70)
(70)
1. Пусть 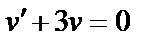
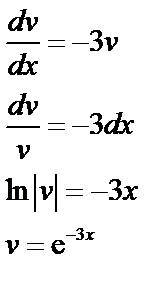
2. Возвращаясь к (70), получаем:
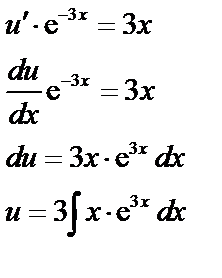
Вычислим 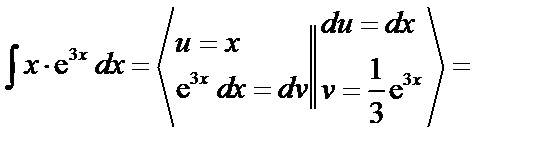
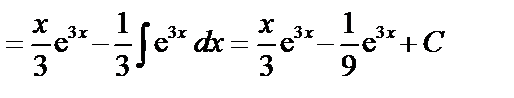
Имеем 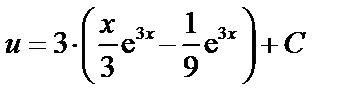
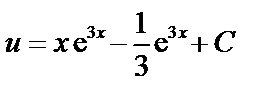
3. Поскольку  , то получаем общее решение
, то получаем общее решение 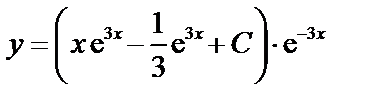 или
или 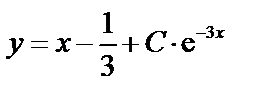 .
.
Ответ: 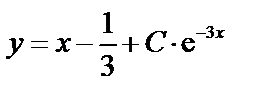 .
.
Задача 3. Найти общее решение уравнения 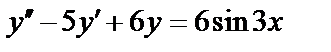 .
.
Решение: 1. Корнями характеристического уравнения 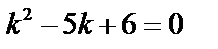 будут
будут 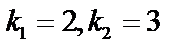 , следовательно,
, следовательно, 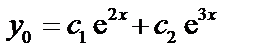 – общее решение соответствующего однородного уравнения.
– общее решение соответствующего однородного уравнения.
2. Так как в правой части уравнения 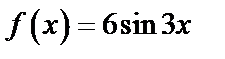 или
или 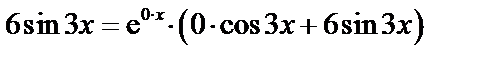 ,
, 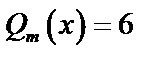 ,
, 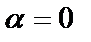 ,
, 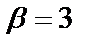 , то
, то
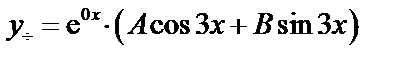 ,
,
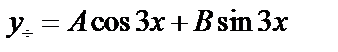 .
.
Найдем 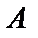 и
и 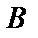 . Для этого вычислим
. Для этого вычислим
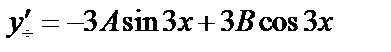 ;
;
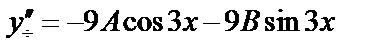 .
.
Подставив значения 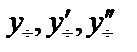 в исходное уравнение, получим тождество
в исходное уравнение, получим тождество
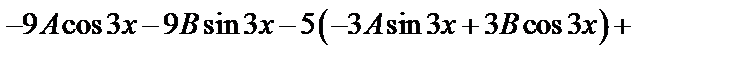
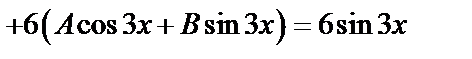
или 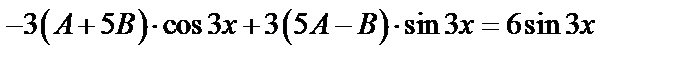 .
.
Приравнивая коэффициенты при 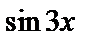 и
и 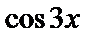 , имеем
, имеем
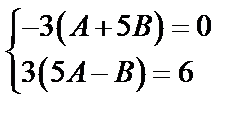
Решая систему, получим 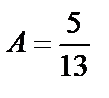 ,
, 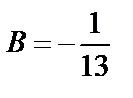 .
.
Частное решение неоднородного уравнения 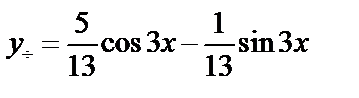 .
.
3. Общее решение 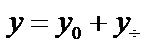 ,
,
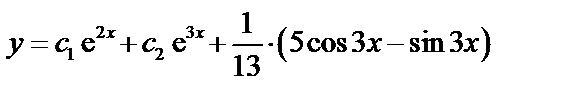 .
.
Ответ: 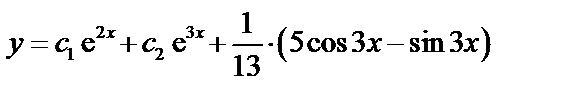 .
.
Задача 4. Написать уравнения кривых, ограничивающих области интегрирования, построить эти области, изменить порядок интегрирования 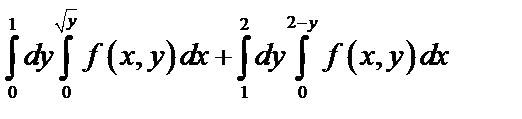 .
.
Решение:
а) Найдем уравнение линий, ограничивающих область интегрирования 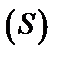 . Для этого приравняем к
. Для этого приравняем к 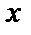 пределы изменения интеграла по переменной
пределы изменения интеграла по переменной 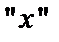 и к
и к 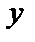 пределы изменения интеграла по переменной
пределы изменения интеграла по переменной 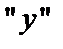 .
.
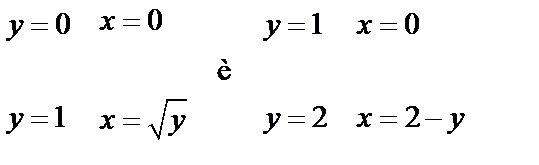
б) Построим область 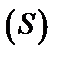 (рис. 15)
(рис. 15)
 |
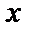 |
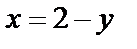 |
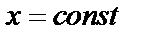 |
| Рис. 15 |
в) Запишем двукратный интеграл с постоянными пределами по 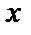 и переменными – по
и переменными – по 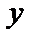 . Проведем сечение
. Проведем сечение 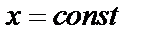 . Прямые входят в область
. Прямые входят в область 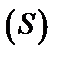 на линии
на линии 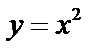 (получили из уравнения
(получили из уравнения 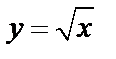 ) и выходят на линии
) и выходят на линии 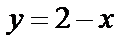 (получили из уравнения
(получили из уравнения 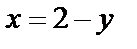 ).
).
Имеем 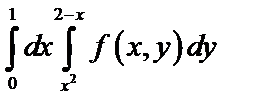 .
.
Ответ: 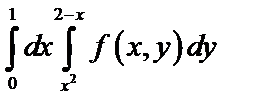 .
.
Задача 5. Вычислить площадь фигуры. ( задана системой неравенств):
задана системой неравенств):
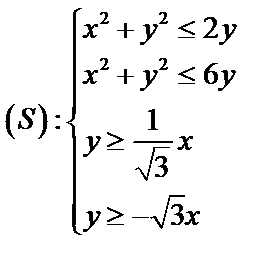
Решение:
а) Построим область  (рис. 16)
(рис. 16)
Уравнения 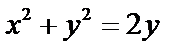 и
и 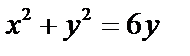 приведем к каноническому виду:
приведем к каноническому виду:
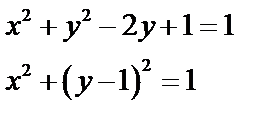
Последнее уравнение задает окружность с центром в т. 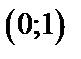 и радиуса
и радиуса 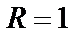 .
.
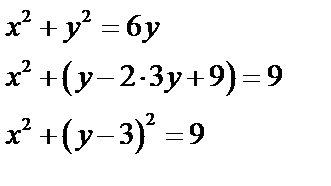
Последнее уравнение задает окружность с центром в т.
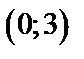 и радиуса
и радиуса 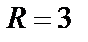 .
.
 |
 |
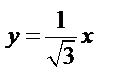 |
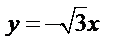 |
 |
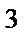 |
| Рис. 16 |
б) Перейдем к полярным координатам: 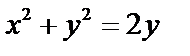 . Подставим
. Подставим 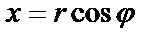 ,
, 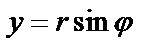 , тогда получим:
, тогда получим:
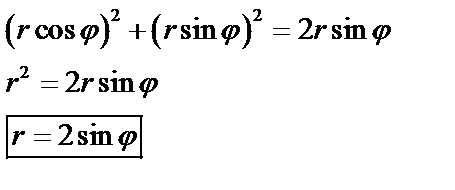
Аналогично,
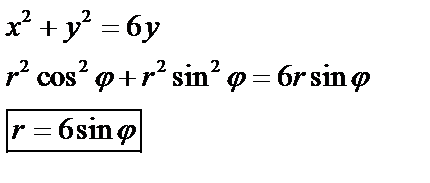
в) Найдем площадь по формуле (47)
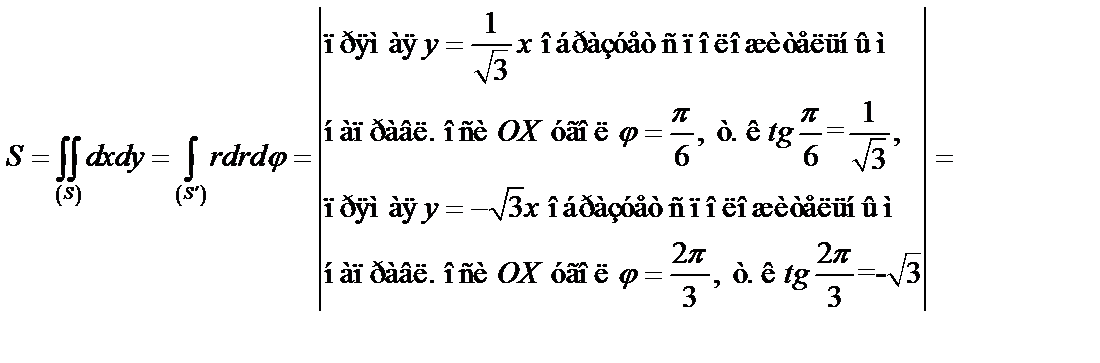
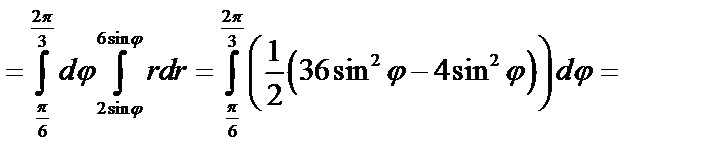
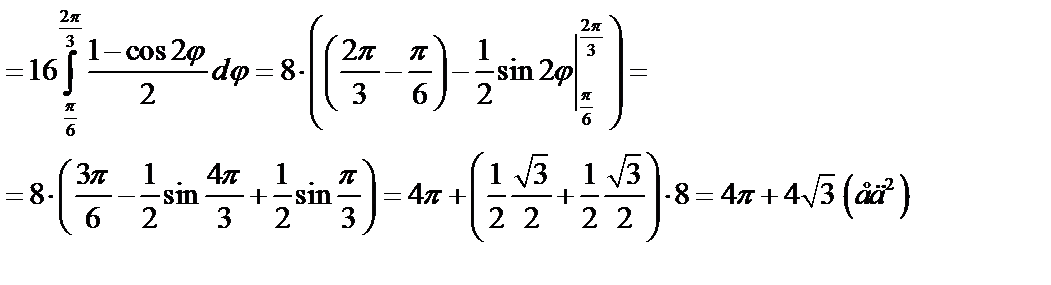
Ответ: 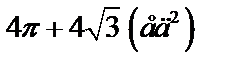 .
.
Задача 6. Вычислить 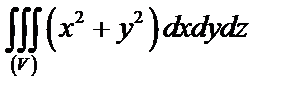 , где
, где
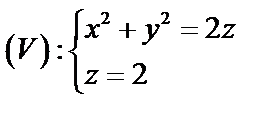
Решение:
а) Построим область интегрирования 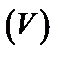 (рис. 17).
(рис. 17).
Уравнение 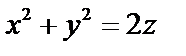 определяет параболоид вращения. Уравнение
определяет параболоид вращения. Уравнение 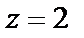 определяет плоскость.
определяет плоскость.
 |
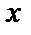 |
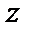 |
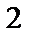 |
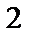 |
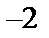 |
| Рис. 17 |
б) Вычислим тройной интеграл в цилиндрических координатах (по формуле 45), полагая
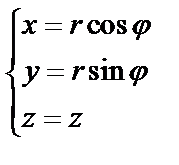 ,
, 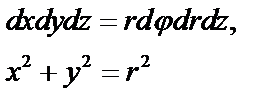
В таком случае
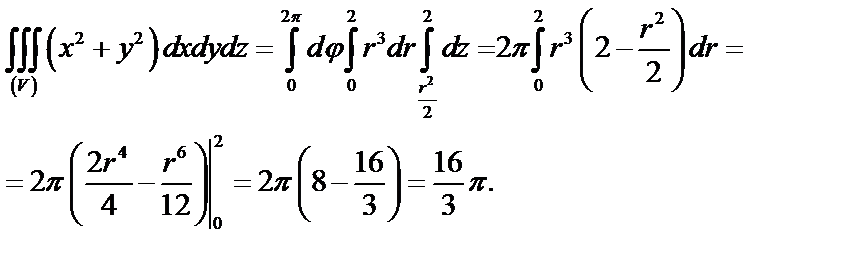
Ответ: 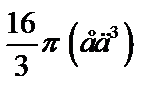 .
.
Задача 7. Найти массу дуги кривой 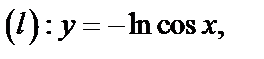
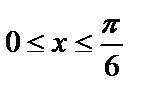 , если плотность:
, если плотность: 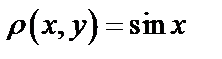 .
.
Решение:
а) Используем формулу (48): 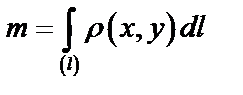 .
.
Найдем 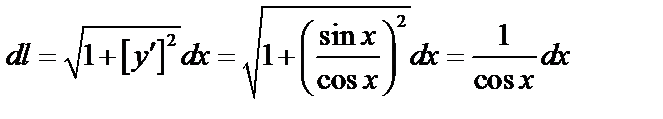
б) Вычислим криволинейный интеграл I рода. Для этого перейдем к определенному интегралу по переменной  , причем
, причем 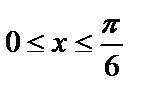 .
.
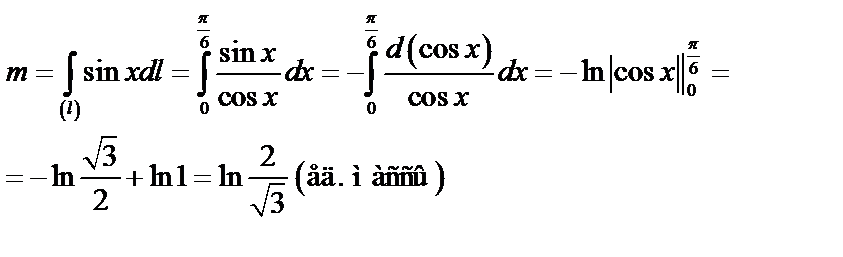
Ответ: 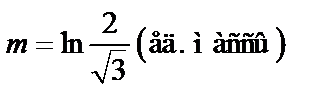 .
.
Задача 8. Вычислить 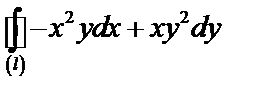 , где
, где 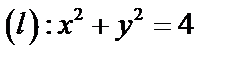 .
.
Решение:
а) Построим окружность 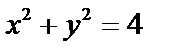 (рис. 18)
(рис. 18)
 |
 |
 |
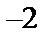 |
| Рис. 18 |
б) Запишем уравнение 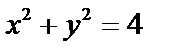 в параметрическом виде:
в параметрическом виде:
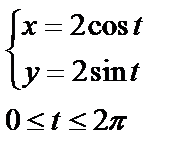 , т.к.
, т.к. 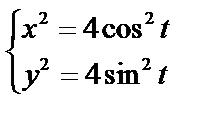 и
и 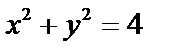
в) Вычислим криволинейный интеграл II-го рода по формуле (49):
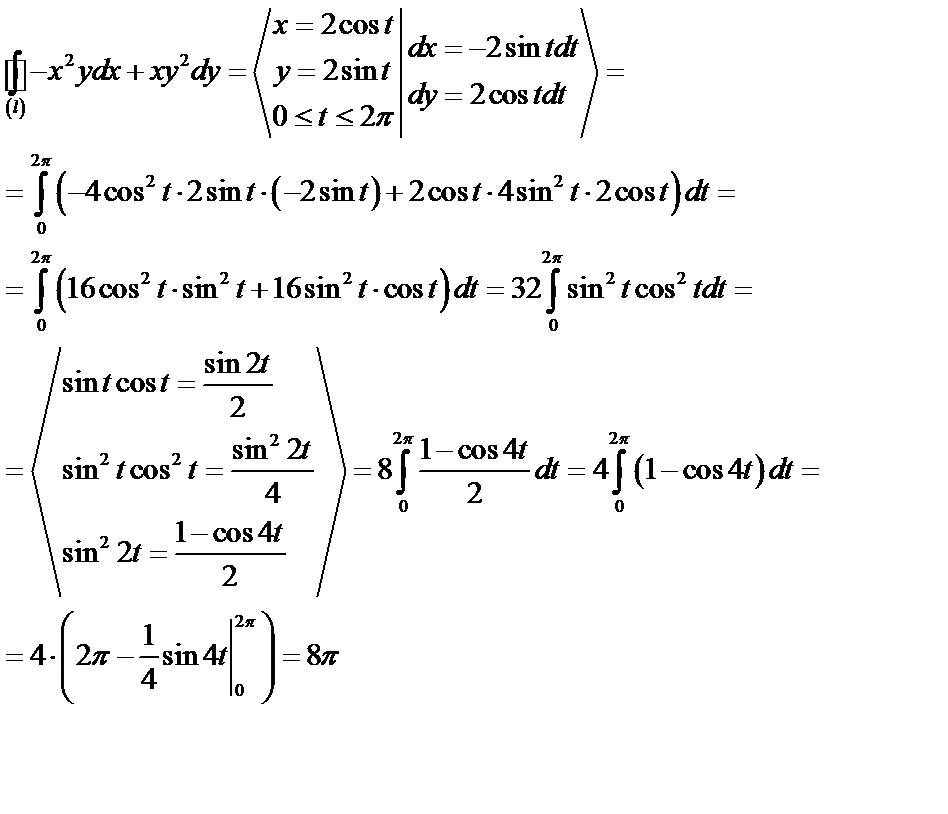
Ответ: 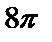 .
.
Задача 9. Найти область сходимости ряда 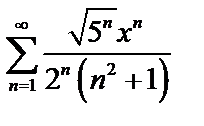 .
.
Решение:
1. Составим ряд из модулей членов данного ряда и применим к нему признак Даламбера
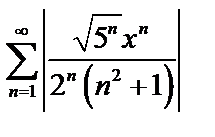
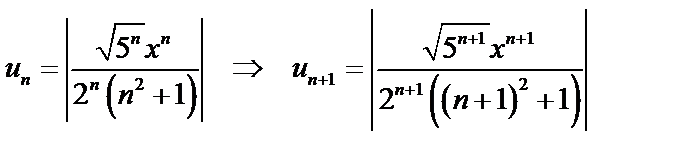
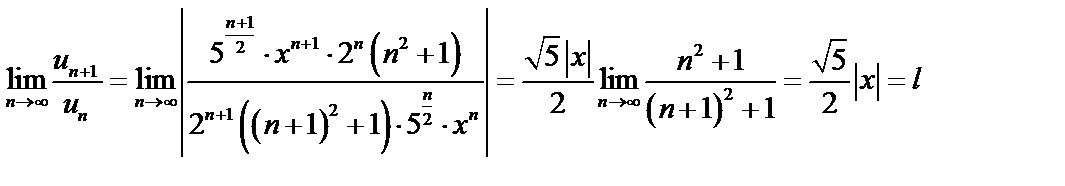
2. При 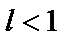 ряд из модулей (а, значит, и исходный) сходится, т.е. надо решить неравенство:
ряд из модулей (а, значит, и исходный) сходится, т.е. надо решить неравенство: 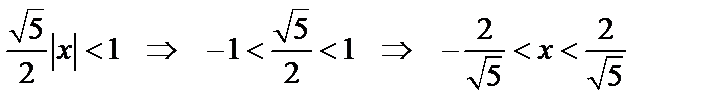 .
.
 |
 |
| сходится |
| расходится |
| расходится |
| ? |
| ? |
3. Исследуем исходный ряд на сходимость в точках 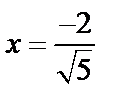 и
и 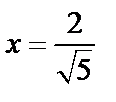 .
.
При 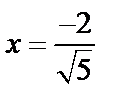 имеем
имеем 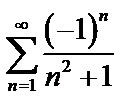 – ряд знакочередующийся.
– ряд знакочередующийся.
Исследуем ряд по признаку Лейбница:
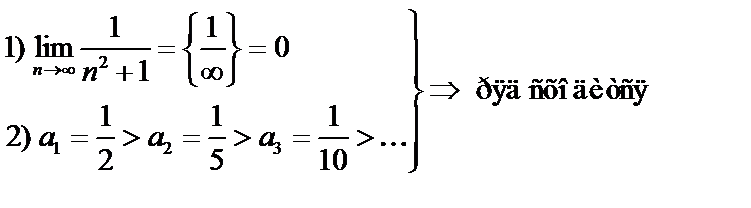
Точка 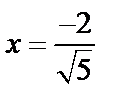 входит в область сходимости.
входит в область сходимости.
При 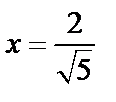 имеем
имеем 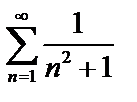 – знакоположительный ряд. Применим к нему признак сравнения (эквивалентности).
– знакоположительный ряд. Применим к нему признак сравнения (эквивалентности).
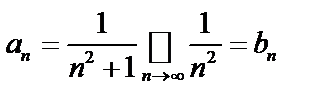 .
.
Так как ряд 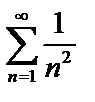 – гармонический
– гармонический  , то он сходится, а значит, и ряд
, то он сходится, а значит, и ряд 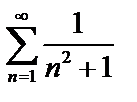 тоже сходится, т.е. точка
тоже сходится, т.е. точка 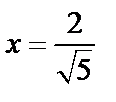 в область сходимости входит.
в область сходимости входит.
Ответ: Область сходимости: 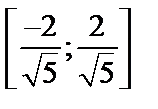 .
.
Задача 10. Разложить функцию 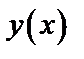 в ряд Фурье по
в ряд Фурье по 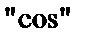
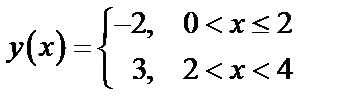
Решение:
1. Строим график на заданном промежутке 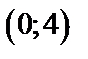 , затем продолжаем функцию графически на
, затем продолжаем функцию графически на 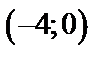 четным образом, т.е. симметрично относительно оси
четным образом, т.е. симметрично относительно оси  , получим промежуток
, получим промежуток 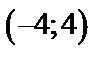 длиной в период, т.е.
длиной в период, т.е. 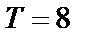 (рис. 19). Достраиваем график на всю ось с периодом
(рис. 19). Достраиваем график на всю ось с периодом 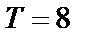 .
.
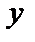 |
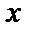 |
| -2 |
| -4 |
| -2 |
| Рис. 19 |
| T=8 |
2. Проверим условия теоремы Дирихле на 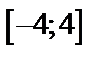
а) кусочно-непрерывна;
б) кусочно-монотонна
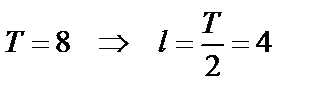 .
.
3. Так как функция четная, то 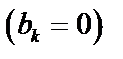 и
и
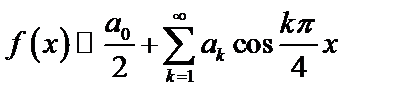 (см. формулы 50), где
(см. формулы 50), где
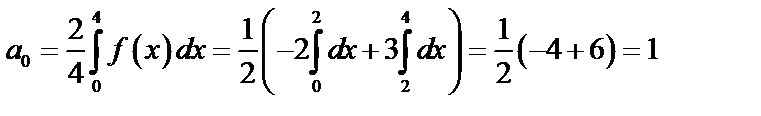 ,
, 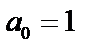
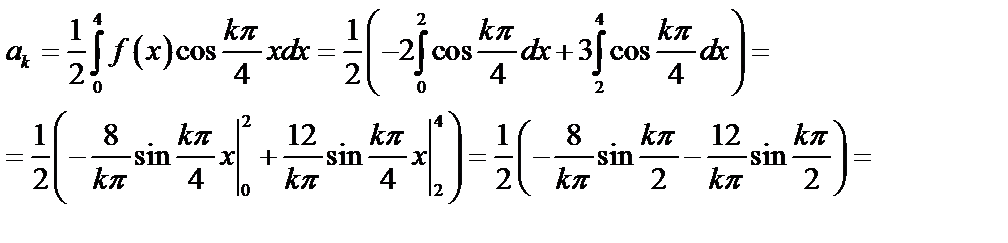
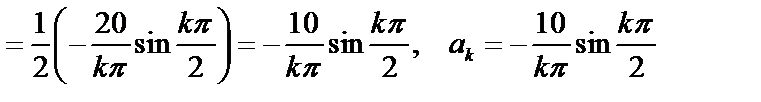 .
.
Таким образом, 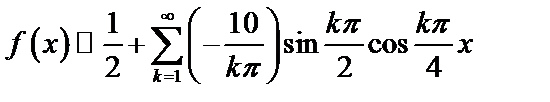 .
.
4. Найдем 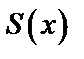 по теореме Дирихле:
по теореме Дирихле:
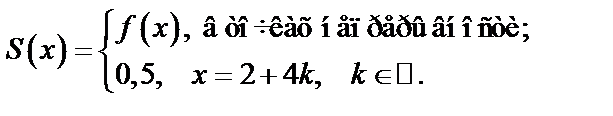
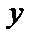 |
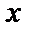 |
| -2 |
| -4 |
| -6 |
| -8 |
| -10 |
| 0,5 |
| -14 |
| -2 |
| Рис. 20 |
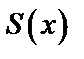 :
: Задача 11. Вычислить расходимость и вихрь в произвольной точке 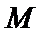 поля градиента скалярного поля
поля градиента скалярного поля 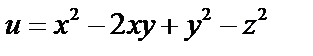 .
.
Решение:
1. Найдем 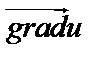 по формуле (52):
по формуле (52):
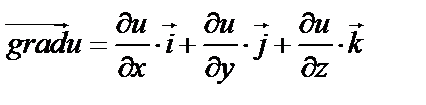
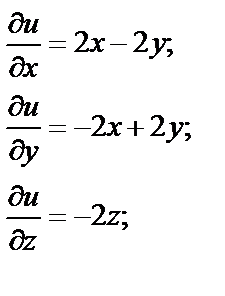
Таким образом, 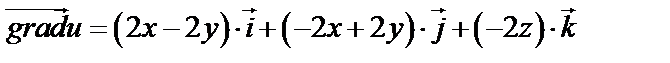 .
.
2. Найдем расходимость (дивергенцию) поля градиента скалярного поля 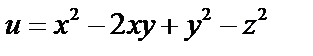 в произвольной точке
в произвольной точке  .
.
Применим формулу (54):
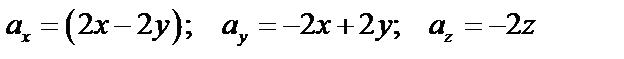 .
.
Т.к. 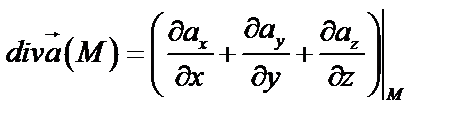 , где
, где 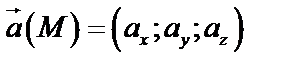 .
.
Найдем
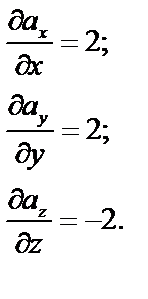
Имеем 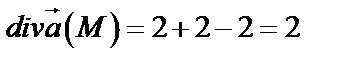 , т.е.
, т.е. 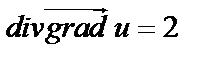
3. Найдем вихрь в произвольной точке 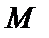 поля градиента скалярного поля
поля градиента скалярного поля 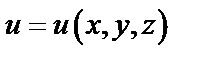 по формуле (57):
по формуле (57):
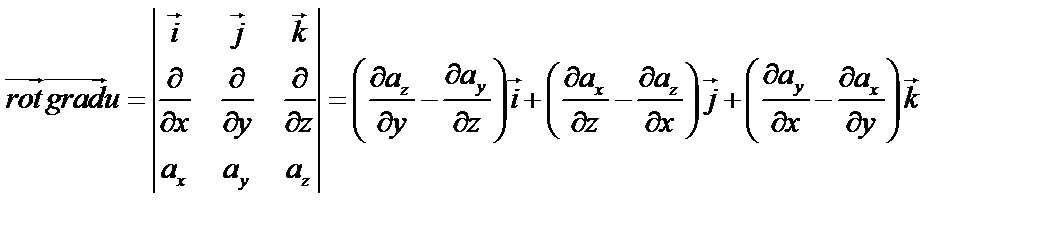
Таким образом, 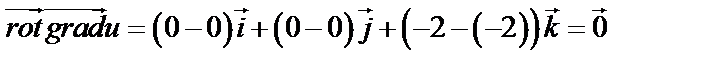 .
.
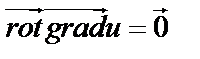 .
.
Ответ: 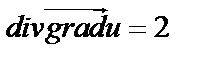 ;
; 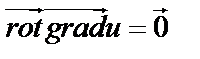 .
.
Задача 12. Дано векторное поле 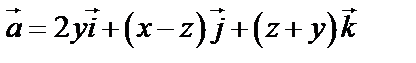 , плоскость
, плоскость 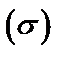 :
: 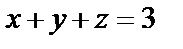 , которая свместно с координатными плоскостями
, которая свместно с координатными плоскостями 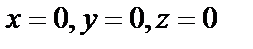 образует пирамиду
образует пирамиду 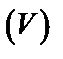 . Найти:
. Найти:
1) поток 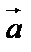 через
через 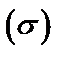 , где
, где 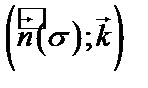 ,
, 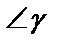 – острый;
– острый;
2) поток 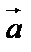 через полную поверхность
через полную поверхность 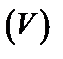 в направлении внешней нормали к ее поверхности (
в направлении внешней нормали к ее поверхности (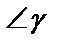 – острый);
– острый);
3) циркуляцию векторного поля 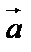 по замкнутому контуру
по замкнутому контуру 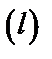 , ограничивающий
, ограничивающий 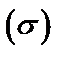 с нормалью
с нормалью 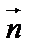 непосредственно;
непосредственно;
4) циркуляцию векторного поля 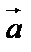 по замкнутому контуру
по замкнутому контуру 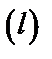 , ограничивающий
, ограничивающий 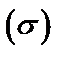 с нормалью
с нормалью 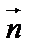 по формуле Стокса.
по формуле Стокса.
Решение:
1) Найдем направляющие косинусы нормали 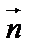 к поверхности
к поверхности 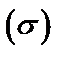 .
.
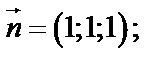
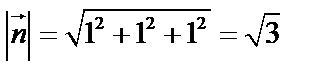 .
.
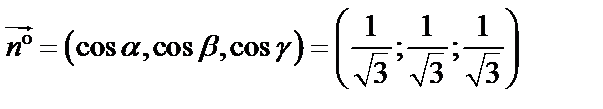
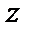 |
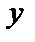 |
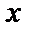 |
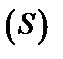 |
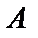 |
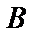 |
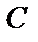 |
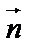 |
| Рис. 21 |
По формуле (53) найдем
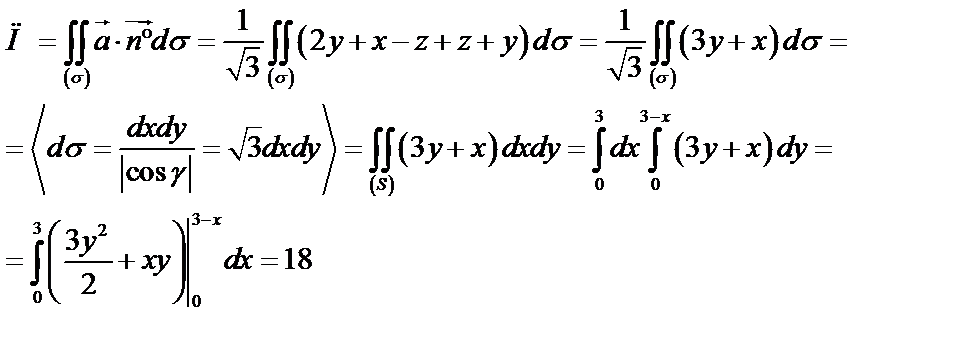
Ответ: 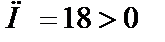 .
.
2) Для нахождения потока через полную поверхность  воспользуемся формулой Остроградского-Гаусса (55):
воспользуемся формулой Остроградского-Гаусса (55): 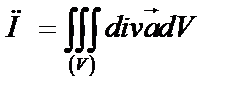 .
.
Найдем 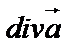 по формуле (54):
по формуле (54):
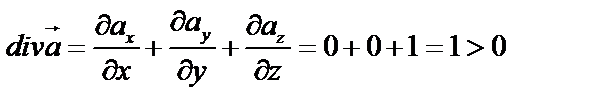 (источник поля).
(источник поля).
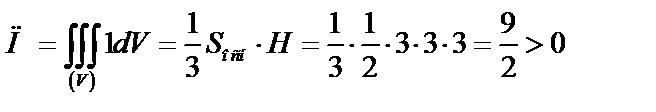 (Из области
(Из области  вытекает жидкости больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости).
вытекает жидкости больше, чем в нее втекает, что указывает на наличие в этой области источников, питающих поток жидкости).
Ответ: 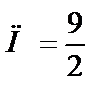 .
.
3) Вычислим циркуляцию  по контуру
по контуру  по формуле (56):
по формуле (56):
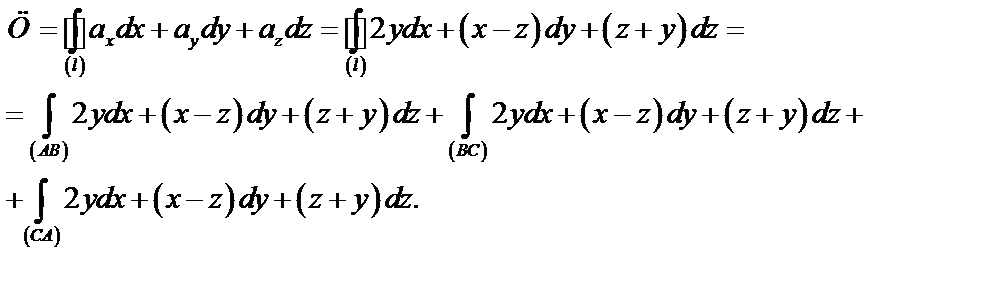
Так как 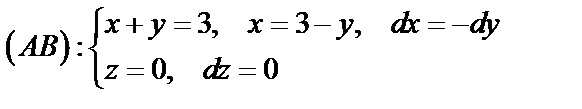
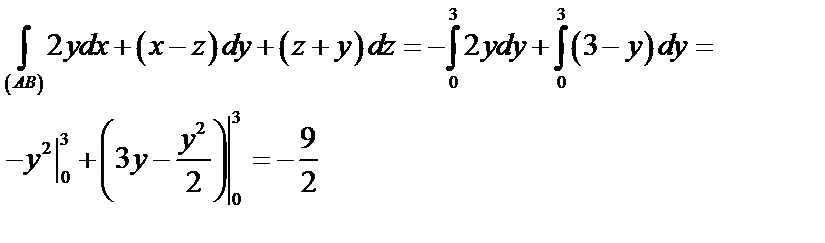
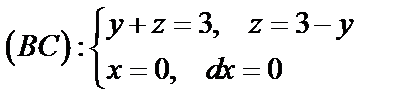
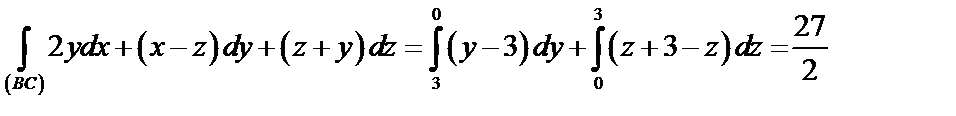
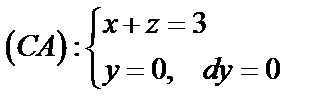
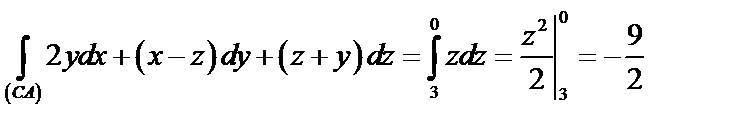
Таким образом, 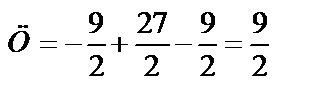 .
.
Ответ: 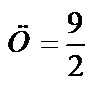 .
.
4) Вычислим циркуляцию по формуле Стокса (58):
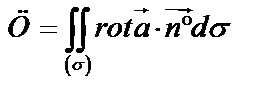 .
.
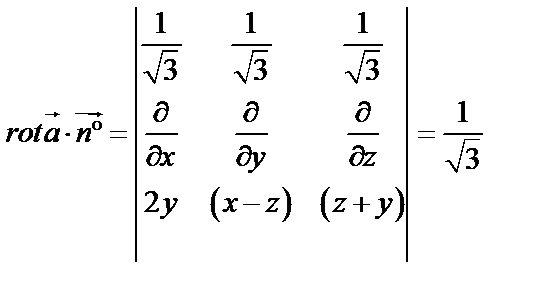
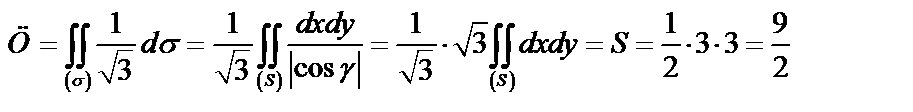 .
.
Ответ: 1) 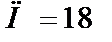 ; 2)
; 2) 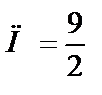 ; 3)
; 3) 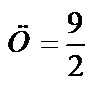 ; 4)
; 4) 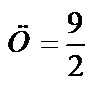 .
.
Задача 13. В компании 10 акционеров, из них три имеют привелигированные акции. На собрании акционеров явилось 6 человек. Найти вероятность того, что среди явившихся акционеров:
а) все трое акционеров с привелигированными акциями отсутствуют;
б) двое присутствуют, и один не явился.
Решение:
а) испытанием является отбор 6 человек из 10 акционеров. Число всех исходов испытания равно числу сочетаний из 10 по 6 (см. формулу 5 в приложении I). 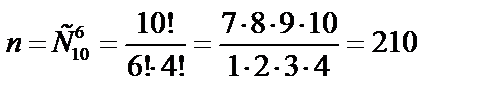 .
.
Пусть событие 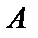 – среди шести человек нет ни одного с привелигированными акциями. Исход, благоприятствующий событию
– среди шести человек нет ни одного с привелигированными акциями. Исход, благоприятствующий событию 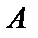 – отбор шести человек среди семи акционеров, не имеющих привелигированных акций. Число всех исходов, благоприятствующих событию
– отбор шести человек среди семи акционеров, не имеющих привелигированных акций. Число всех исходов, благоприятствующих событию 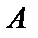 , будет
, будет 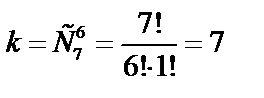 . Искомая вероятность по формуле (59) равна
. Искомая вероятность по формуле (59) равна 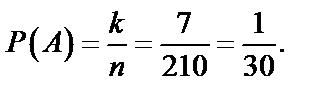
б) Пусть событий 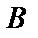 – среди шести явившихся акционеров двое с привелигированными акциями, а остальные четыре – с общими акциями.
– среди шести явившихся акционеров двое с привелигированными акциями, а остальные четыре – с общими акциями.
Число всех исходов 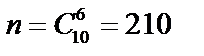 .
.
Число способов выбора двух человек из необходимых трех 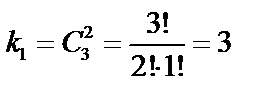 . Число способов выбора оставшихся четырех акционеров среди семи с общими акциями
. Число способов выбора оставшихся четырех акционеров среди семи с общими акциями 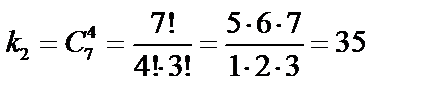 . Тогда число способов отбора по правилу произведения
. Тогда число способов отбора по правилу произведения 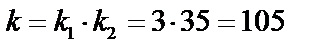 .
.
Искомая вероятность по формуле (59) равна 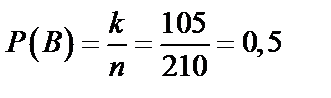 .
.
Задача 14. Среди поступающих на сборку деталей с первого автомата 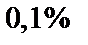 бракованных, со второго –
бракованных, со второго – 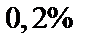 , с третьего –
, с третьего – 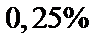 , с четвертого –
, с четвертого – 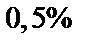 . Производительности их относятся как
. Производительности их относятся как 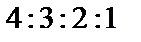 соответственно. Взятая деталь оказалась стандартной. Найти вероятность того, что она изготовлена на четвертом автомате.
соответственно. Взятая деталь оказалась стандартной. Найти вероятность того, что она изготовлена на четвертом автомате.
Решение:
Обозначим через 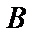 событие –
событие – 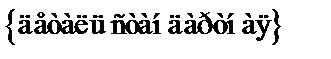 . Гипотезами являются
. Гипотезами являются 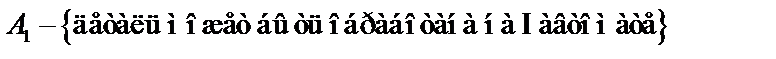 ,
,
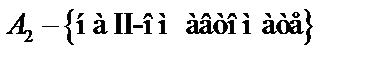 ,
,
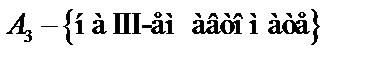 ,
,
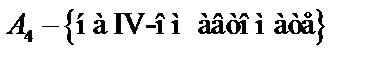 .
.
Вероятность того, что стандартную деталь обработали на четвертом автомате, определим по формуле Байеса (61):
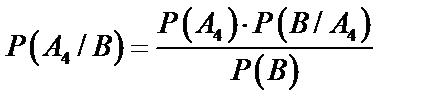 ,
, 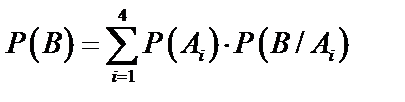 .
.
Т.к. производительности автоматов относятся как 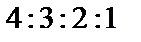 , то вероятность гипотез такова:
, то вероятность гипотез такова: 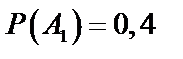 ;
; 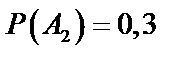 ;
; 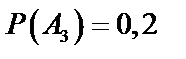 ;
; 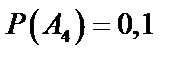 . По условию задачи известны вероятности брака для соответствующего автомата, а нас интересуют вероятности противоположных событий. Поэтому
. По условию задачи известны вероятности брака для соответствующего автомата, а нас интересуют вероятности противоположных событий. Поэтому
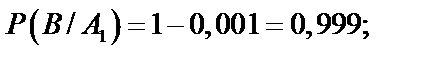
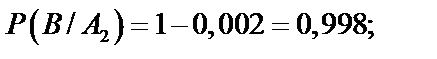
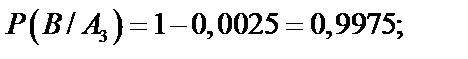
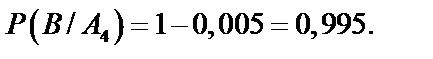
Искомая вероятность равна
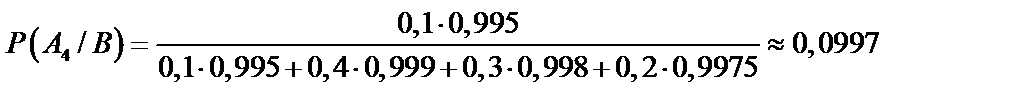 .
.
До испытания вероятность гипотезы  была
была 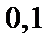 , а после того, как произошло событие
, а после того, как произошло событие 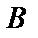 , вероятность этой гипотезы изменилась и стала равной
, вероятность этой гипотезы изменилась и стала равной 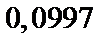 .
.
Задача 15. В случаях а, б и в рассматривается серия из 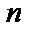 независимых итспытаний с двумя исходами в каждом – «успех» или «неуспех». Вероятность «успеха» равна
независимых итспытаний с двумя исходами в каждом – «успех» или «неуспех». Вероятность «успеха» равна 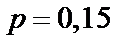 , «неуспеха» –
, «неуспеха» – 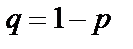 в каждом испытании.
в каждом испытании.
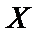 – число «успехов» в
– число «успехов» в 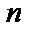 испытаниях. Требуется:
испытаниях. Требуется:
1) для случая а (малого 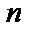 ) построить ряд распределения, функцию распределения
) построить ряд распределения, функцию распределения 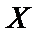 , найти
, найти 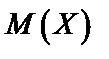 ,
, 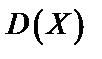 и
и 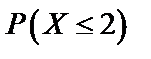 .
.
2) для случая б (большого 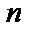 и малого
и малого 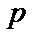 ) найти
) найти 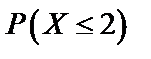 приближенно с помощью распределения Пуассона.
приближенно с помощью распределения Пуассона.
3) для случая в (большого 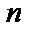 ) найти вероятность
) найти вероятность 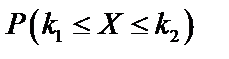 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
а) 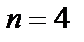 ,
, 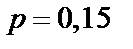 ;
;
б) 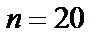 ,
, 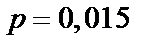 ;
;
в) 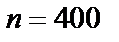 ,
, 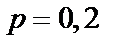 ,
, 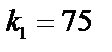 ,
, 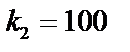 .
.
Решение:
а)
 | |||||
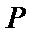 | 0,522 | 0,3685 | 0,0975 | 0,0115 | 0,0005 |
Найдем по формуле Бернулли (62):
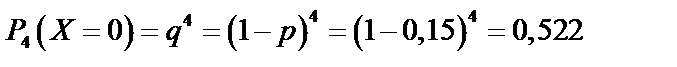
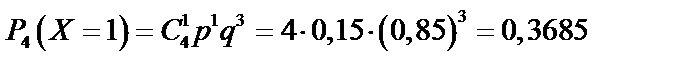
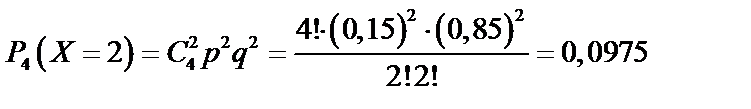
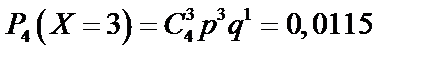
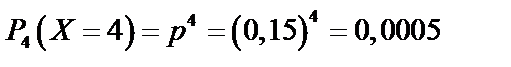
Найдем 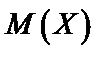 по формуле (65):
по формуле (65):
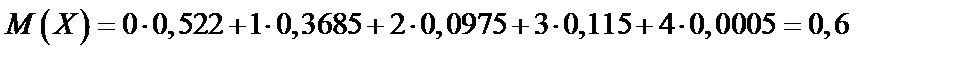 ; или
; или 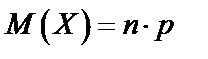 ;
; 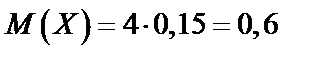 .
.
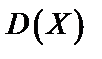 по формуле (66):
по формуле (66):
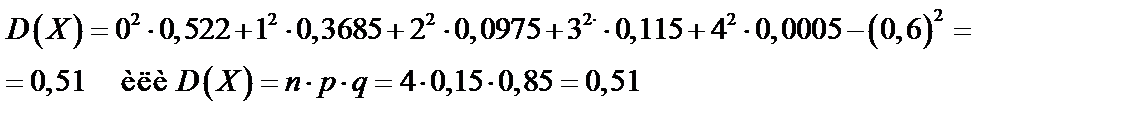
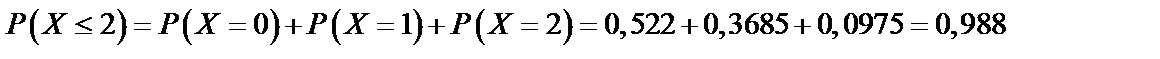
Найдем функцию распределения 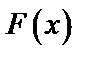 и построим график.
и построим график.

Построим график этой функции.
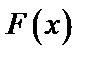 |
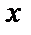 |
б) 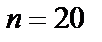 ,
, 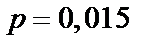 ,
, 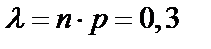 (по формуле (63))
(по формуле (63))
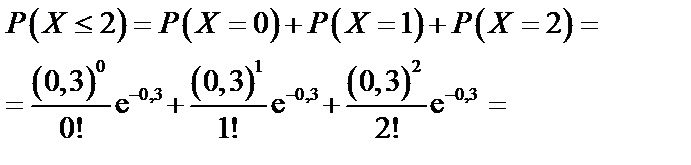
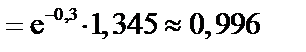
в) 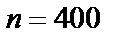 ,
, 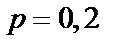 ,
, 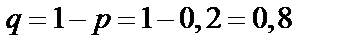
Найдем 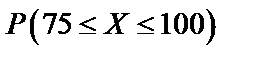 по формуле (64).
по формуле (64).
Имеем 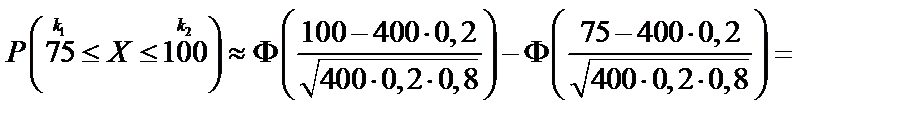
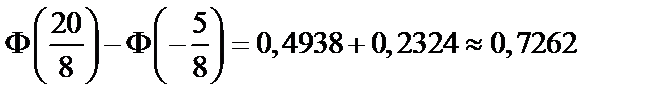 .
.
Ответ: а) 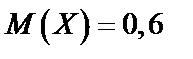 ;
; 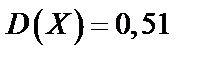 ;
; 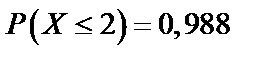 ;
;
б) 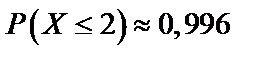 ;
;
в) 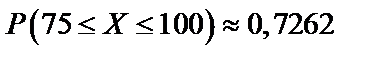 .
.
Задача 16. Случайная величина  задана плотностью распределения:
задана плотностью распределения:
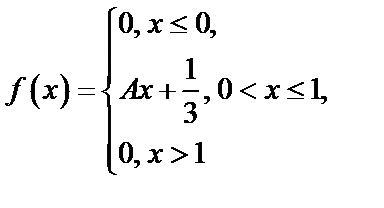
Требуется:
а) Найти коэффициент 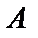 ;
;
б) Найти функцию распределения 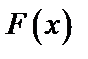 ; построить графики
; построить графики 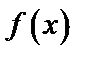 и
и 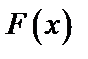 ;
;
в) найти математическое ожидание 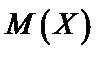 , дисперсию
, дисперсию 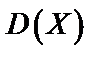 и квадратическое отклонение
и квадратическое отклонение 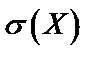 .
.
Решение:
а) Плотность распределения 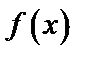 должна удовлетворять условиям:
должна удовлетворять условиям: 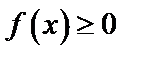 ,
, 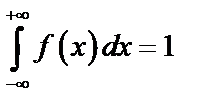 .
.
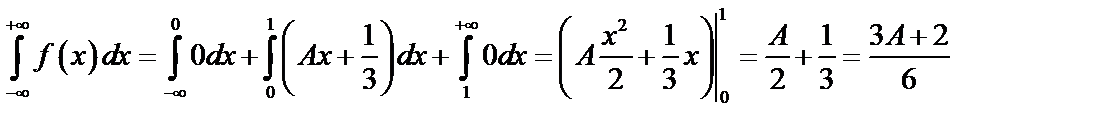
Так как 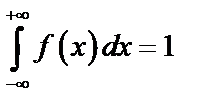 , то
, то 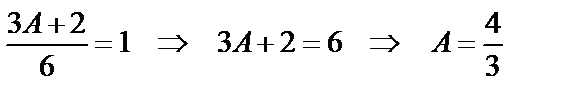 .
.
Таким образом,
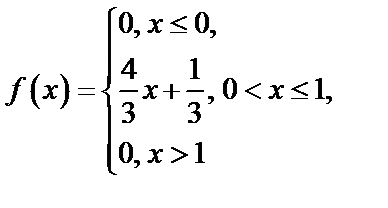
б) Для нахождения функции распределения  воспользуемся формулой
воспользуемся формулой  .
.
При 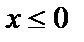 ,
, 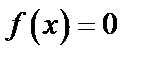 , то
, то 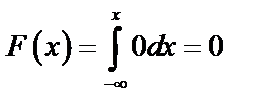 .
.
При 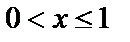 ,
, 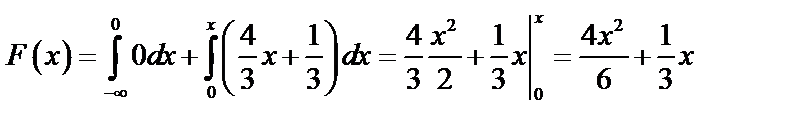
При 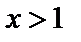 ,
, 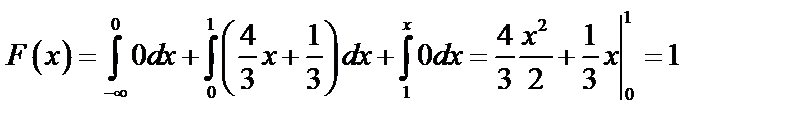 .
.
Итак,
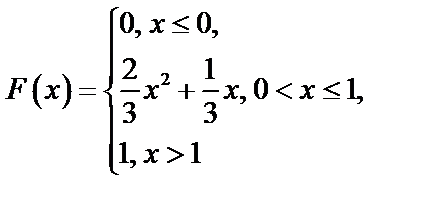
Построим графики 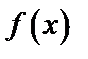 и
и 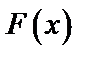 .
.
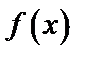 |
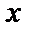 |
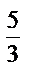 |
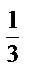 |
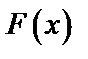 |
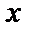 |
в) Для непрерывной случайной величины 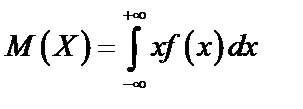 ,
,
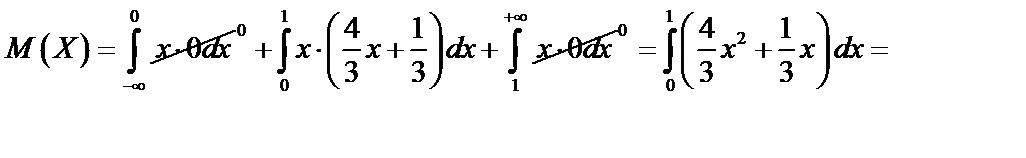
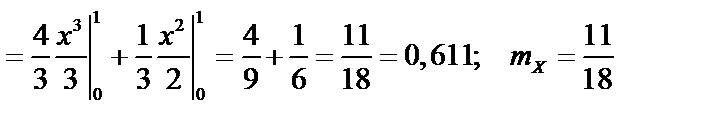
Для непрерывной случайной величины
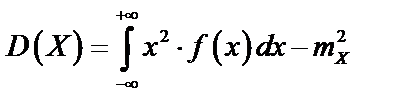 .
.
Имеем 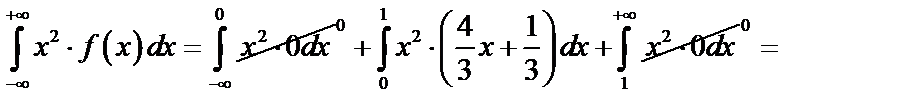
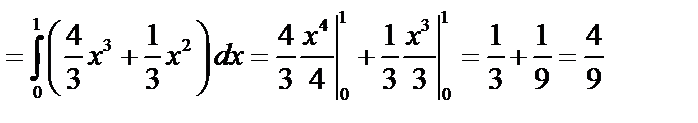
Тогда 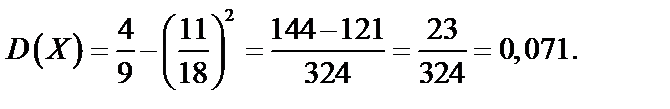
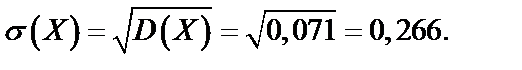
Ответ: а) 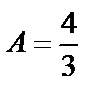 ;
;
б) 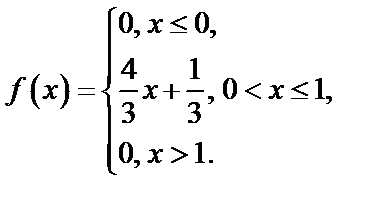
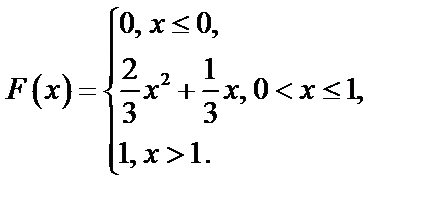
в) 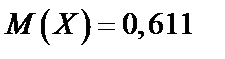 ;
; 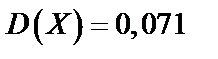 ;
; 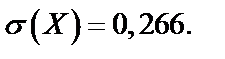
Задача 17. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали равна 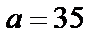 , среднее квадратическое отклонение
, среднее квадратическое отклонение 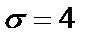 . Требуется:
. Требуется:
а) составить функцию плотности вероятностей;
б) найти вероятность того, что диаметр наудачу взятой детали будет больше 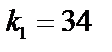 и меньше
и меньше 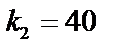 ;
;
в) найти вероятность того, что диаметр детали отклонится от стандартной длины не более чем на 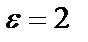 .
.
Решение:
а) 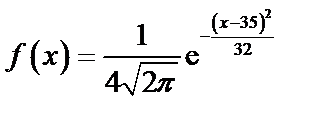 (по формуле 67);
(по формуле 67);
б) 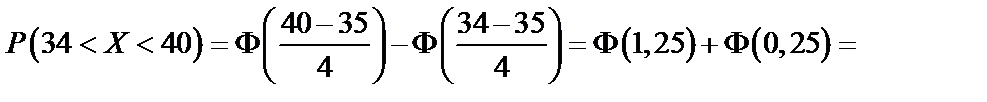
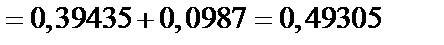 (по формуле 68);
(по формуле 68);
в) 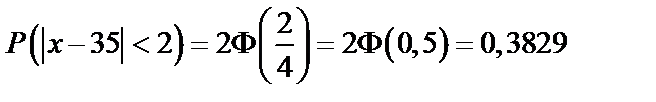 (по формуле 69).
(по формуле 69).
Замечание: Значения функции 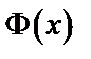 находятся по таблице в приложении II.
находятся по таблице в приложении II.
 2015-05-13
2015-05-13 1643
1643
