П р и м е р 1. Даны множества: 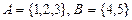 . Найти декартово произведение
. Найти декартово произведение 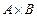
Решение. 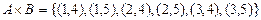 .
.
П р и м е р 2. 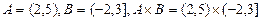 . Изобразить на координатной плоскости
. Изобразить на координатной плоскости 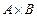 .
.
Решение. Изобразим множество 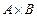 на координатной плоскости, построив прямые х = 2, х = 5, у = –2 (штриховыми линиями) и у =3. Итак, декартово произведение
на координатной плоскости, построив прямые х = 2, х = 5, у = –2 (штриховыми линиями) и у =3. Итак, декартово произведение 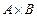 изображается множеством точек прямоугольника CDPL, причём С (2, –2), D (2, 3), Р (5, 3), L(5, –2). Точки отрезков CD и CL и PL исключаются, так как
изображается множеством точек прямоугольника CDPL, причём С (2, –2), D (2, 3), Р (5, 3), L(5, –2). Точки отрезков CD и CL и PL исключаются, так как 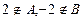 и
и 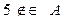 . (Рис. 24).
. (Рис. 24).
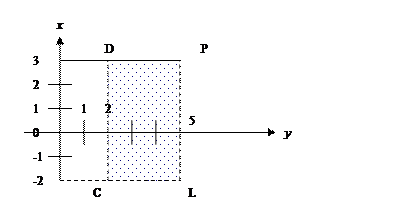
Рис. 24.
П р и м е р 3. 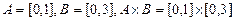 .
.
Решение. 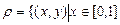 и
и 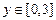 и
и 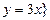 – бинарное отношение, заданное на паре множеств А и В.
– бинарное отношение, заданное на паре множеств А и В.
П р и м е р 4. Пусть 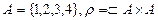
Решение. Зададим отношение 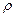 различными способами:
различными способами:
1) с помощью характеристического свойства
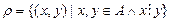
2) перечислением элементов 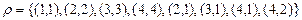 ;
;
3) Напомним, что графом называется конечное множество точек, некоторые пары из которых, соединены линиями, причём каждая пара точек может быть соединена одной линией. Если на линиях указаны направления, то граф называется ориентированным.
Изобразим элементы множества А точками и проведём стрелки с началом х и концом у для всех таких упорядоченных пар (х, у), что 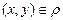 . Если
. Если 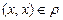 , то на графе рисуется петля. Получим такой граф (рис.25):
, то на графе рисуется петля. Получим такой граф (рис.25):
|
|
|
 |
Рис. 25
4) таблицей: если 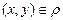 , то на пересечении строки, соответствующей х, и столбца, соответствующего у, ставится знак «+».
, то на пересечении строки, соответствующей х, и столбца, соответствующего у, ставится знак «+».
| у х | ||||
| + | ||||
| + | + | |||
| + | + | |||
| + | + | + |
5) графиком:

Рис. 26
П р и м е р 5. Определите какими свойствами обладает отношение параллельности на множестве П прямых плоскости.
Решение. Отношение «||» на множестве П прямых плоскости является рефлексивным, симметричным, транзитивным, но не является антисимметричным и антирефлексивным. Действительно:
1. 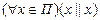 – истинно (отношение «||» рефлексивно);
– истинно (отношение «||» рефлексивно);
2. 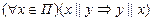 – истинно (отношение «||» симметрично);
– истинно (отношение «||» симметрично);
3. 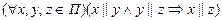 – истинно (отношение «||» транзитивно);
– истинно (отношение «||» транзитивно);
4. 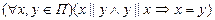 – ложно (отношение «||» не антисимметрично);
– ложно (отношение «||» не антисимметрично);
5. 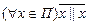 – ложно (отношение «||» не антирефлексивно).
– ложно (отношение «||» не антирефлексивно).
Замечание. Если бинарное отношение 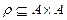 задано на конечном множестве А и
задано на конечном множестве А и
1) если 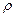 рефлексивно, то в каждой точке (изображающей элемент множества А) на графе есть петля;
рефлексивно, то в каждой точке (изображающей элемент множества А) на графе есть петля;
2) если 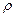 симметрично, то на графе нет односторонних стрелок;
симметрично, то на графе нет односторонних стрелок;
3) если 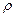 антисимметрично, то на графе нет двухсторонних стрелок (не считая петель);
антисимметрично, то на графе нет двухсторонних стрелок (не считая петель);
4) если 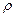 транзитивно, то для любых трёх точек, соответствующих
транзитивно, то для любых трёх точек, соответствующих 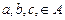 , если из а идёт стрелка в b, из b идёт стрелка в с, то из а идёт стрелка в b;
, если из а идёт стрелка в b, из b идёт стрелка в с, то из а идёт стрелка в b;
5) если 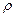 антирефлексивно, то на графе отсутствуют петли.
антирефлексивно, то на графе отсутствуют петли.
П р и м е р 6. Проверить свойства отношения 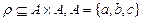 , если
, если 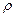 задано графом (Рис. 27):
задано графом (Рис. 27):

Рис. 27
Решение. 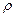 – симметрично, все остальные свойства не выполняются.
– симметрично, все остальные свойства не выполняются.
П р и м е р 7. Запишите на языке предикатов определение нерефлексивного, несимметричного и нетранзитивного бинарного отношения и приведите примеры таких отношений.
|
|
|
Решение. а) Бинарное отношение, заданное на множестве А, естественно назвать не рефлексивным, если 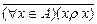 , что равносильно высказыванию
, что равносильно высказыванию 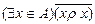 или
или 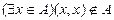 . Например, пусть
. Например, пусть 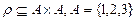 . Бинарное отношение
. Бинарное отношение 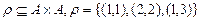 не рефлексивно, так как существует элемент
не рефлексивно, так как существует элемент 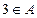 , такой что
, такой что 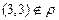 .
.
б) Заметим, что если бинарное отношение 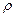 рассматривать во множестве R, то симметричность
рассматривать во множестве R, то симметричность 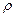 можно интерпретировать так: график отношения
можно интерпретировать так: график отношения 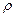 имеет биссектрису первого и третьего координатных углов своей осью симметрии.
имеет биссектрису первого и третьего координатных углов своей осью симметрии.
Бинарное отношение 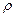 , заданное на множестве А не будет симметричным тогда и только тогда, когда
, заданное на множестве А не будет симметричным тогда и только тогда, когда
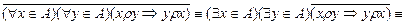
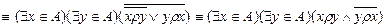 или
или 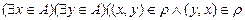 .
.
Например, отношение 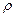 , рассмотренное в пункте а) не является симметричным, так как существуют два числа 1 и 3 во множестве А, такие что
, рассмотренное в пункте а) не является симметричным, так как существуют два числа 1 и 3 во множестве А, такие что 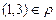 , но
, но 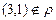 .
.
в) Бинарное отношение 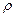 , заданное на множестве А не транзитивно тогда и только тогда, когда
, заданное на множестве А не транзитивно тогда и только тогда, когда
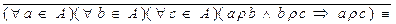
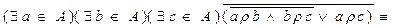
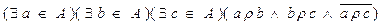 .
.
Например, бинарное отношение: «две точки на плоскости имеют, по крайней мере, одну одинаковую координату» рефлексивно, симметрично, но не транзитивно. Точки А(2;4) и В(2,6) имеют одинаковую координату 2, точки В(2;6) и С(8;6) имеют одинаковую координату 6, но точки А(2;4) и С(8;6) не имеют одинаковых координат.
Этот пример показывает, что из рефлексивности и симметричности не следует транзитивность.
П р и м е р 8. Приведите пример бинарного отношения, которое является отношением эквивалентности.
Решение. а) Ранее рассмотренное отношение параллельности, заданное на множестве прямых плоскости, является отношением эквивалентности;
б) Отношение перпендикулярности, заданное на множестве прямых плоскости не является эквивалентностью, так как не рефлексивно и не транзитивно.
Замечание. Выясним, не являются ли некоторые условия эквивалентности (рефлексивность, симметричность, транзитивность) излишними. Быть может из выполнения двух из них следует третье? Было уже показано, что из рефлексивности и симметричности не следует транзитивность. Может быть, из симметричности и транзитивности следует рефлексивность? Отрицательный ответ на этот вопрос даёт следующий контрпример: 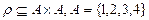 , бинарное отношение
, бинарное отношение 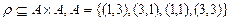 симметрично, транзитивно, но не рефлексивно.
симметрично, транзитивно, но не рефлексивно.
П р и м е р 9. Пусть А = {0, 1, 2, 3, 4, 5, 6}, 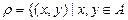 ; х и у при делении на 3 дают одинаковые остатки}. Является ли ρ отношением эквивалентности, если да, то найдите все классы эквивалентности.
; х и у при делении на 3 дают одинаковые остатки}. Является ли ρ отношением эквивалентности, если да, то найдите все классы эквивалентности.
Решение. А = {0, 1, 2, 3, 4, 5, 6}, 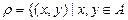 ; х и у при делении на 3 дают одинаковые остатки}. Изобразим граф данного бинарного отношения (рис.28):
; х и у при делении на 3 дают одинаковые остатки}. Изобразим граф данного бинарного отношения (рис.28):

Рис. 28
Получили три класса эквивалентности:
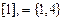 ,
, 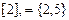 ,
, 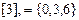
П р и м е р 10. Найдите фактор-множество А относительно эквивалентности ρ, если а)отношение ρ из примера 9; б) отношение ρ – отношение параллельности на множестве прямых плоскости.
Решение. а) В примере 9 имеем: 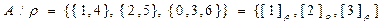 ;
;
б) Пусть П – множество прямых плоскости. Отношение «||» на множестве П является эквивалентностью. 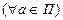 класс эквивалентности
класс эквивалентности 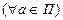
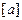 представляет собой пучок параллельных прямых.
представляет собой пучок параллельных прямых.
П р и м е р 11. Пусть 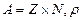 – бинарное отношение, заданное на множестве А, такое, что
– бинарное отношение, заданное на множестве А, такое, что 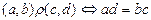 . Определите классы эквивалентности множества А по отношению
. Определите классы эквивалентности множества А по отношению 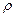 .
.
Решение. Очевидно, что 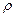 – эквивалентность. Поэтому
– эквивалентность. Поэтому 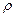 определяет некоторое разбиение А. Классы эквивалентности этого разбиения называются рациональными числами, таким образом, множество всех рациональных чисел есть множество
определяет некоторое разбиение А. Классы эквивалентности этого разбиения называются рациональными числами, таким образом, множество всех рациональных чисел есть множество 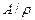 , которое обычно обозначают Q. Условимся, тот класс эквивалентности, которому принадлежит упорядоченная пара
, которое обычно обозначают Q. Условимся, тот класс эквивалентности, которому принадлежит упорядоченная пара 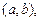 обозначать
обозначать 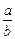 . Тогда мы получим
. Тогда мы получим 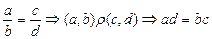 .
.
П р и м е р 12. Являются ли бинарные отношения а) отношение  на множестве действительных чисел; б) отношение
на множестве действительных чисел; б) отношение  на множестве всех подмножеств множества U; в) отношение
на множестве всех подмножеств множества U; в) отношение  на множестве натуральных чисел отношением порядка?
на множестве натуральных чисел отношением порядка?
Решение. а) Отношение 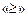 на множестве R является отношением порядка, так как истинны три высказывания:
на множестве R является отношением порядка, так как истинны три высказывания:
|
|
|
1) 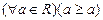 (
(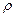 – рефлексивно,);
– рефлексивно,);
2) 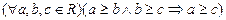 (
(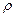 – транзитивно);
– транзитивно);
3) 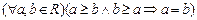 (
(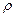 – антисимметрично).
– антисимметрично).
б) Отношение 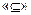 (включения) на В(U) (множестве всех подмножеств множества U) является отношением порядка, так как оно рефлексивно, транзитивно и антисимметрично
(включения) на В(U) (множестве всех подмножеств множества U) является отношением порядка, так как оно рефлексивно, транзитивно и антисимметрично
в) Отношение 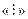 (делится нацело) является отношением порядка на N (множестве натуральных чисел), так как оно рефлексивно, транзитивно и антисимметрично.
(делится нацело) является отношением порядка на N (множестве натуральных чисел), так как оно рефлексивно, транзитивно и антисимметрично.
П р и м е р 13. Является ли отношение 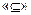 на множестве В(U) отношением линейного порядка?
на множестве В(U) отношением линейного порядка?
Решение. Отношение 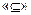 на множестве В(U) (где U содержит не менее двух различных элементов) не является отношением линейного порядка, т.к., например, для подмножеств { a } и { b } множества U ={ а,b } не выполняется условие линейности.
на множестве В(U) (где U содержит не менее двух различных элементов) не является отношением линейного порядка, т.к., например, для подмножеств { a } и { b } множества U ={ а,b } не выполняется условие линейности.
П р и м е р 14. Рассмотрим бинарное отношение 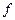 , заданное графом (Рис.29). Найдите область определения, множество значений бинарного отношения
, заданное графом (Рис.29). Найдите область определения, множество значений бинарного отношения 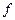 . Является ли
. Является ли 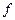 –функцией?
–функцией?

Рис.29
Решение. 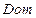
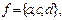 Im
Im 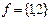 . Из каждой точки Dom f выходит ровно одна стрелка. Следовательно, бинарное отношение
. Из каждой точки Dom f выходит ровно одна стрелка. Следовательно, бинарное отношение 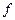 является функцией.
является функцией.
П р и м е р 15. Пусть 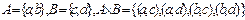 . Являются ли функциями следующие бинарные отношения, заданные перечислением:
. Являются ли функциями следующие бинарные отношения, заданные перечислением: 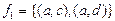 ;
; 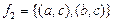 ;
; 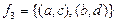 .
.
Решение. 1) 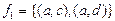 не является функцией, так как
не является функцией, так как 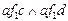 , но
, но 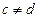 ;
;
2) 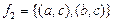 – функция (по определению);
– функция (по определению);
3) 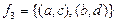 – функция (по определению).
– функция (по определению).
П р и м е р 16. Являются ли бинарные отношения заданные графами на рисунках 29, 30, 31 отображениями? Инъективны, сюръективны ли они?
Решение. 1) Функция, изображённая на Рис. 29 не является отображением, не инъективна, не сюръективна, а следовательно, не биективна.
2) Бинарное отношение 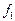 (Рис. 30) является сюръективной функцией, так как
(Рис. 30) является сюръективной функцией, так как 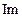
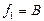 , но не является инъективной, так как
, но не является инъективной, так как 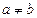 , но
, но 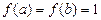 .
.
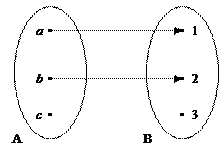
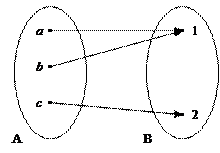
Рис. 30 Рис. 31
3)Бинарное отношение 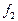 (Рис. 31) является инъективной функцией (по определению), но не является сюръективной, так как
(Рис. 31) является инъективной функцией (по определению), но не является сюръективной, так как 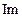
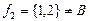 . Функции
. Функции 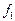 и
и 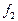 являются отображениями, т.к. их области определения совпадают с А.
являются отображениями, т.к. их области определения совпадают с А.
 2015-05-13
2015-05-13 2872
2872
