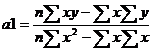Формальные методы разукрупнения отдельных факторов

При построении модели детерминированного разложения анализируемого показателя по взаимодействующим факторам используется ряд формальных приемов разукрупнения отдельных факторов. Различают следующие приемы моделирования:

1. Метод удлинения факторной системы, он предусматривает удлинение числителя исходной модели путем расчленения одного или более факторов на составляющие элементы по схеме аддитивной зависимости и получения аддитивной модели с новым набором показателей – факторов.

2. Метод формального разложения факторной системы, он предусматривает удлинение знаменателя исходной модели путем расчленения одного и более факторов, не составляющих однородные элементы по схеме аддитивной зависимости.

3. Метод расширения факторной системы, он предусматривает преобразование исходной модели путем умножения числителя и знаменателя элементов исходной модели на один и более вводимый показатель фактора с последующим получением мультипликативной модели с новым набором факторов.
, где a/c = d1; b/c = d2

4. Стохастические методы экономического анализа.
Это методы корреляционного и регрессионного анализа. Они применяются тогда, когда невозможно заранее определить теоретические и строго определенный характер зависимости между факторными и результативным показателями. При проведении корреляционного анализа вводится предположение о характере зависимости между результативными и факторными признаками. Простейший вариант – это линейная зависимость результативного показателя «у» от фактора «х», тогда связь между ними определяется следующим уравнением.

Ух = а0 + а1х

Таким образом, первым этапом проведения корреляционного и регрессионного анализа является введение предположения о форме связи между результатом и факторами (кроме линейно, связь может быть квадратической, кубической, логарифмической, экспонинциальной). Связь между фактором и результатом будет вполне установлена если будут определены параметры уравнения регрессии а0 и а1. Они определяются в результате решения системы уравнений:

;

После расчета параметров а0 и а1, прежде чем использовать синтезированное уравнение регрессии анализа и прогнозирования, необходимо проверить тесноту связи между фактором и результатом и установить является ли она существенной.

При прямолинейной форме связи между фактором и результатом теснота связи определяется по формуле линейного коэффициента корреляции.

Рассчитанные значения коэффициента корреляции “r” интерпретируются в соответствии со шкалой:

Значение коэффициента корреляции	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Сила связи	слабая	умеренная	заметная	сильная	весьма сильная

Пример 4.

Имеется следующая информация по однотипным предприятиям торговли о возрасте торгового оборудования и затратах на его ремонт. Необходимо построить модель зависимости расходов на ремонт от возраста оборудования.

№ предприятия n	Возраст оборудования х	Затраты на ремонт у
1	4	1,5
2	5	2,0
3	5	1,4
4	6	2,3
5	8	2,7
6	10	4,0
7	8	2,3
8	7	2,5
9	11	6,6
10	6	1,7

Для определения параметров а0, а1 и коэффициента регрессии ‘r’ используется рабочая таблица следующей структуры:

№ п/п	у	х	х2	ху	у2
1	1,5	4	16	6	2,25
2	2,0	5	25	10	4,0
3	1,4	5	25	7	1,96
4	2,3	6	36	13,8	5,29
5	2,7	8	64	21,6	7,29
6	4,0	10	100	40	16
7	2,3	8	64	18,4	5,29
8	2,5	7	49	17,5	6,25
9	6,6	11	121	72,6	43,56
10	1,7	6	36	10,2	2,89
∑	27	70	536	217,2	94,78

;
Уравнение регрессии: у = а0 + а1*х
у = -1,576 + 0,611 * х

Проверим существенность связи между показателем у и х. Рассчитаем коэффициент корреляции.

Значение коэффициента корреляции свидетельствует о высокой силе связи между фактором и результатом, следовательно, синтезированная регрессионная модель пригодна для практического использования.

Пусть необходимо определить затраты на ремонт оборудования, возрост которого составляет 15 лет.
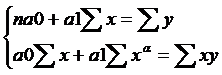