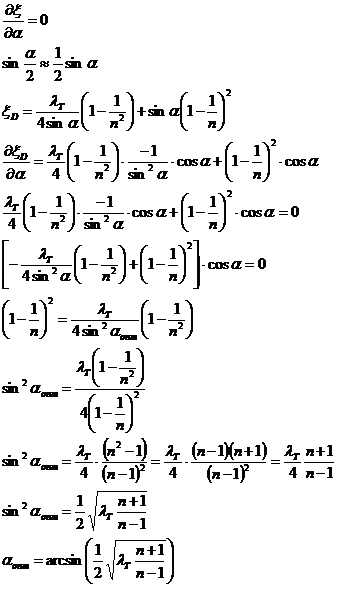Местные сопротивления

В гидравлике местные сопротивления делятся на 2 группы:

Внезапные.
Постепенные (плавные).

В каждую группу входят:

Расширение
Сужение
Поворот

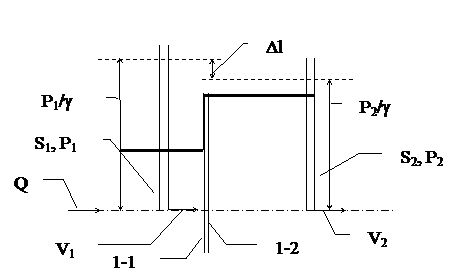
5.1. Внезапное расширение канала.

Рис. 5.1
Рассматривается турбулентный режим течения
Коэффициент внезапного расширения: ,
Для идеальной жидкости:

Потери полного давления при внезапном расширении
Примем следующие допущения:

α1=1, α2=1 - турбулентное течение
касательными напряжениями пренебрегаем из-за малой длины
Р=Р1 давление на боковой стенке (эксперимент).

Тогда

Для контура, ограниченного сечениями 1-1, 1-2 и боковой стенкой канала запишем уравнения сохранения количества движения в проекции на ось канала:

Учитывая уравнения неразрывности V1S1=V2S2, после преобразований получим
(5.1)
Эта формула носит наименование теоремы Борда-Карно.

Вводя понятие степени расширения канала n = S2/S1, будем иметь

Тогда коэффициент сопротивления
(5.2)

Этот результат хорошо согласуется с опытами.

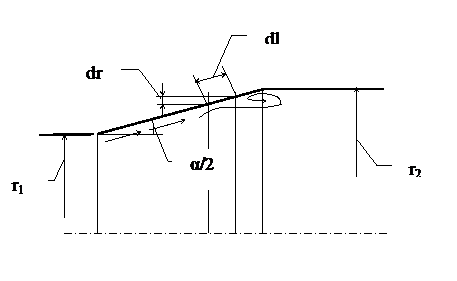
5.2. Постепенное расширение канала. Диффузор

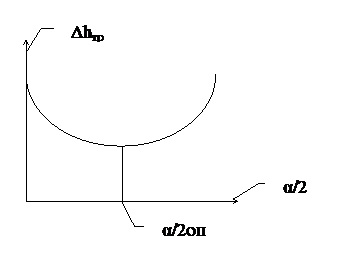
Рис. 5.2

Определим коэффициент местных потерь диффузора. Представив, что потери полного напора складываются из двух составляющих. Потери на трение и потери на вихреобразование.

VS=const VS=V1S1,

, где во – вихреобразование, вр – внезапное расширение.

к – коэффициент смягчения. Для диффузоров с малым углом полураствора (⁰) к = sin α. Тогда:

(5.3)

Из формулы (5.3) следует, что существует оптимальный угол полураствора диффузора, соответствующий минимальному гидравлическому сопротивлению. Это утверждение подтверждает рис. 5.3.

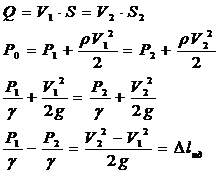
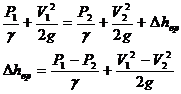
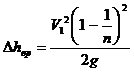
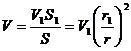
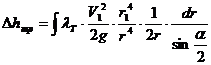
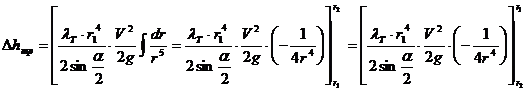
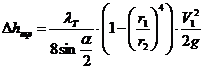
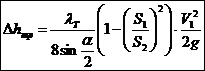
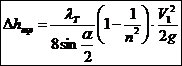
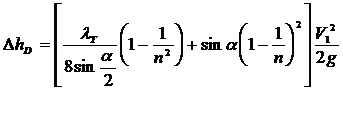
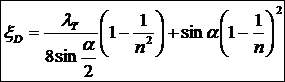Рис. 5.3