Пример 4.8

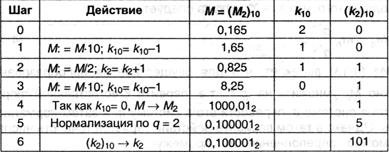
Выполнить преобразование Х₁₀=16,5₁₀→ X₂.

Перевод можно осуществить отдельно для целой и дробной части, а затем их объединить - этот результат послужит эталоном для проверки нового алгоритма. Легко получить, что 16₁₀ = 10000₂, а 0,5₁₀= 0,1₂; следовательно, 16,5₁₀= 10000,1₂= (0,100001∙2¹⁰¹)₂.

Алгоритм Rеаl_1 начинает функционировать после нормализации исходного числа; для этой цели можно воспользоваться алгоритмом Normа, в результате начальными значениями будут М₁₀ = 0,165; k₁₀ = 2. Результаты операций будем заносить в таблицу:

Окончательно имеем: Х₂ = (0,100001∙2¹⁰¹)₂.

Подобным же будет алгоритм преобразования Х₁₀ → Х₂ и при k_p < 0.

Последовательность действий при обратном переводе Х₂→ Х₁₀ отчасти противоположна только что рассмотренной; для k_p ≥ 0 она представлена в виде блок-схемы на рис.4.6. Нормализация в конце (после k = 0) производится при необходимости.